前言

视频讲解在我女朋友的B站『隐马尔可夫链预测问题-从维特比到SLAM』

在上一篇文章《终于有人把隐马尔可夫链的前向后向算法讲懂了！》中，我们讲解了隐马尔科夫链中三个基本问题中的概率计算问题的前向后向求解方法：

1. 概率计算问题：给定模型参数$\lambda =(A,B,\pi )$和观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1​,x2​,...,xn​}计算在模型参数$\lambda$下观测到x的概率$P(x|\lambda )$(评估模型和观测序列之间的匹配程度)

2. 预测问题：给定模型$\lambda =(A,B,\pi )$和观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1​,x2​,...,xn​}，求使得$P(y|x,\lambda )$最大的状态观测序列 y = { y 1 , y 2 , . . . , y n } y=\{y_1,y_2,...,y_n\} y={y1​,y2​,...,yn​}(根据观测序列推断最有可能的状态序列)

3. 学习问题：给定观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1​,x2​,...,xn​}，调整模型参数$\lambda =(A,B,\pi )$，使得该序列出现的概率$P(x|\lambda )$最大(训练模型使其更好地描述观测序列)

这篇文章将主要讲解维特比算法，维特比算法是用来解决预测问题的主要算法，其核心思想是动态规划，这个问题与SLAM问题相似，都是获得一组观测序列(地图点)，然后求解一组状态(机器人位姿)，使得在该位姿下获得该观测的概率最大，最后简要说明学习问题的求解算法。

1.预测问题-维特比算法

主要思想：利用动态规划求解概率最大路径，这里一条路径对应着一个状态序列。

如果最优路径$y\ast$在t时刻通过结点$y_t\ast$，那么这条路径从起始结点到结点$y_t\ast$的路径中,局部路径$y_{1:t}\ast$一定是最优的。(每个结点$y_t\ast$对应一个最优路径)

假定从起始时刻到t时刻上各个状态的最优路径已经找到，那么在计算从起始时刻到t+1时刻上的某个状态$s_j$的最优路径时，只需要考虑从起始时刻到上一时刻所有N个状态$s_i$的最优路径，以及从si到sj的“距离”。

我们定义中间变量${\delta }_t(i)$：在t时刻，隐马尔可夫链沿着一条路径到达状态i，并输出观测序列的最大概率。

路径变量${\varphi }_t(i)$：表示该路径上状态i的前一个状态。

这样说可能很晦涩，我们实例演示一下就很容易明白：

1. 假设只有第一个观测-红球，那么最可能得到这个观测的状态是0还是1呢？我们分别计算它们的概率：假设第一个状态为0，概率为：${\delta }_1(0)=\pi (0)\ast B_{00}=0.25$;假设第一个状态为1，概率为：${\delta }_1(1)=\pi (1)\ast B_{10}=0$.显然如果只有一个观测，最优状态是0.

2. 加入一个状态，第二个观测为黑球，第二个状态可能为0/1，我们分别计算第二个状态为0/1情况下，得到观测为黑球的概率：

• 如果第二个状态为0，它可能由第一个状态为0/1转移而来，这时我们要取一个概率更大的情况：${\delta }_2(0)=max({\delta }_1(0)\ast A_{00}\ast B_{01},{\delta }_1(1)\ast A_{10}\ast B_{01})=0$,两种情况概率一样大，记录最优前一个节点${\varphi }_2(0)=0,1$；

• 如果第二个状态为1，它可能由第一个状态为0/1转移而来，这时我们要取一个概率更大的情况：${\delta }_2(1)=max({\delta }_1(0)\ast A_{01}\ast B_{11},{\delta }_1(1)\ast A_{11}\ast B_{11})=0$,第一种情况更大，记录最优前一个节点${\varphi }_2(1)=0$

3. 依次类推，我们最终计算出了最后一个节点的情况：${\delta }_5(0)=max({\delta }_4(0)\ast A_{00}\ast B_{00},{\delta }_4(1)\ast A_{10}\ast B_{00})=0.015625$，${\varphi }_5(0)=1$；${\delta }_5(1)=max({\delta }_4(0)\ast A_{01}\ast B_{10},{\delta }_4(1)\ast A_{11}\ast B_{10})=0$，${\varphi }_5(0)=0，1$；

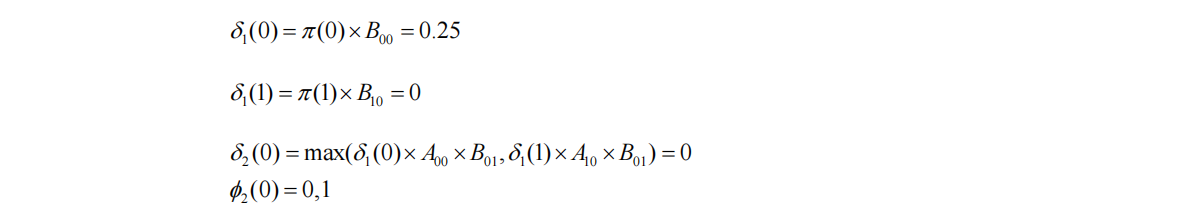
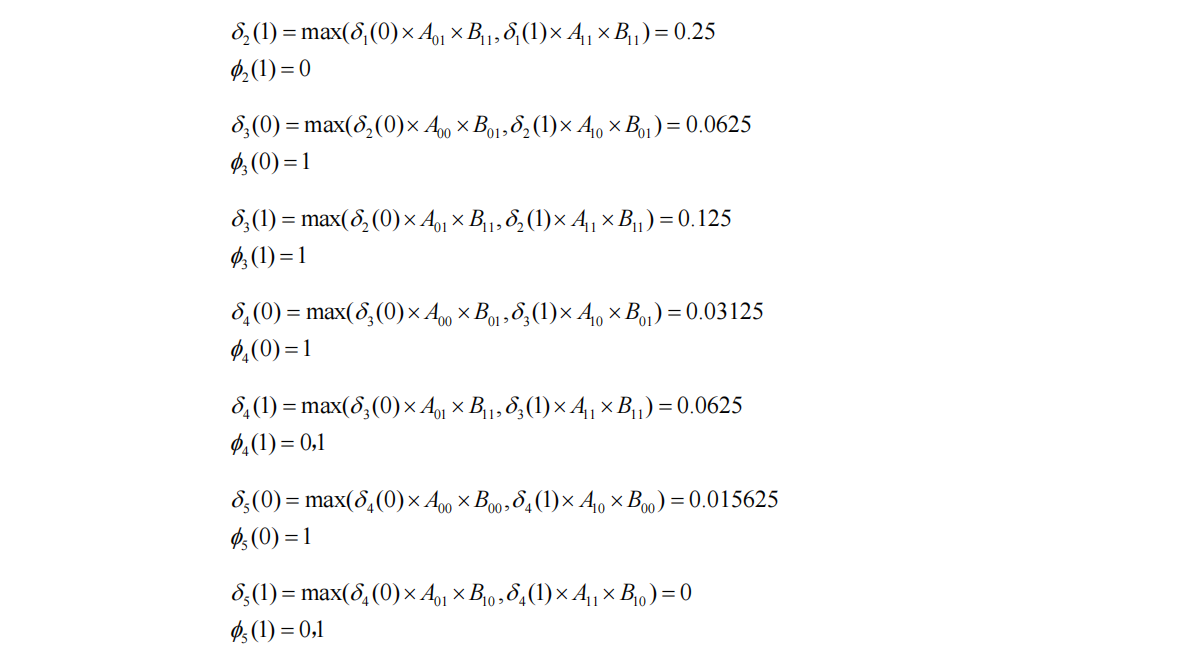
4. 回溯：我们发现最后一个节点${\delta }_5(0)$概率更大，我们确定最后一个状态为0更好，然后根据${\varphi }_5(0)=1$回溯，其指向前一个最优状态${\delta }_4(1)$，所以第4个状态确定为1，然后再根据${\varphi }_4(1)=1$回溯，指向前一个最优状态${\delta }_3(0)或$\delta_3(1)$，然后我们对两条路径分别重复上述回溯，就可以得到最终路径：

0->1->0->1->0或0->1->1->1->0

2.学习问题

学习问题的主要解决目标是学习参数，主要方法是用模式识别中基于参数估计的方法区估计其中的参数，常用的方法有：基于参数估计的极大似然估计、贝叶斯估计；基于半参数估计的EM算法，分为有监督方法和无监督方法。

（1）有监督方法

训练数据包含𝑆个长度相同的观测序列和对应的状态序列$\{(x_1,y_1),(x_2,y_2),...,(x_s,y_s)\}$，利用极大似然法估计隐马尔可夫模型的参数。也就是P（X,Y）最大似然估计。

（2）无监督方法

将观测序列看作观测数据𝒳，状态序列看作不可观测的隐数据𝒴，隐马尔可夫模型等价
于含有隐变量的概率模型。

相应的参数学习可以由EM算法实现

总结

通过三篇文章，我们详细的介绍了马尔科夫链中的相关概念，以及三个基本问题的解法，马尔科夫链是各个领域应用十分广泛的数学工具，其结合了图论和概率论的相关算法模型，特别是在SLAM领域，很多现代的算法都是在马尔科夫链基础上发展而来，希望大家通过这三篇文章的讲解，可以比较好的理解相关内容！