代码随想录算法训练营第二九天 | 递增子序列、排列-编程知识

代码随想录算法训练营第二九天 | 递增子序列、排列

递增子序列

不能使用之前的去重逻辑！

同一父节点下的同层上使用过的元素就不能再使用了

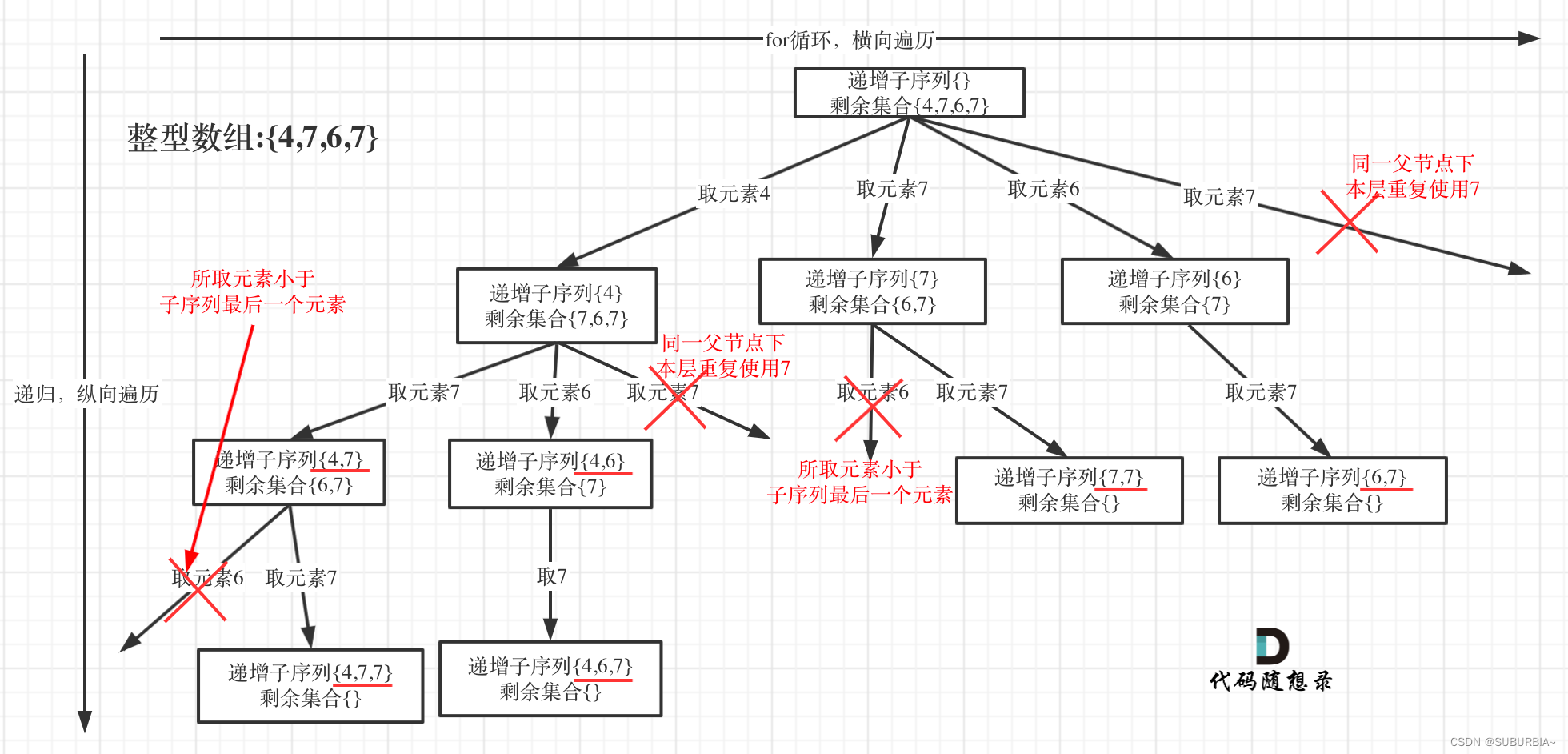
在这里插入图片描述
题目要求递增子序列大小至少为2，终止条件要限定。

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0);return result;}private void backTracking(int[] nums, int startIndex) {if (path.size() > 1) {    // 至少有两个元素 result.add(new ArrayList<>(path));}if (startIndex >= nums.length) {return;}// 存储去重元素的哈希表HashSet<Integer> hs = new HashSet<>();for (int i = startIndex; i < nums.length; i++) {if(!path.isEmpty() && path.get(path.size() -1) > nums[i] || hs.contains(nums[i])) {continue;}hs.add(nums[i]);  // 记录这个元素在本层用过了，本层后面不能再用了path.add(nums[i]);backTracking(nums, i + 1);path.removeLast();}}
}

全排列

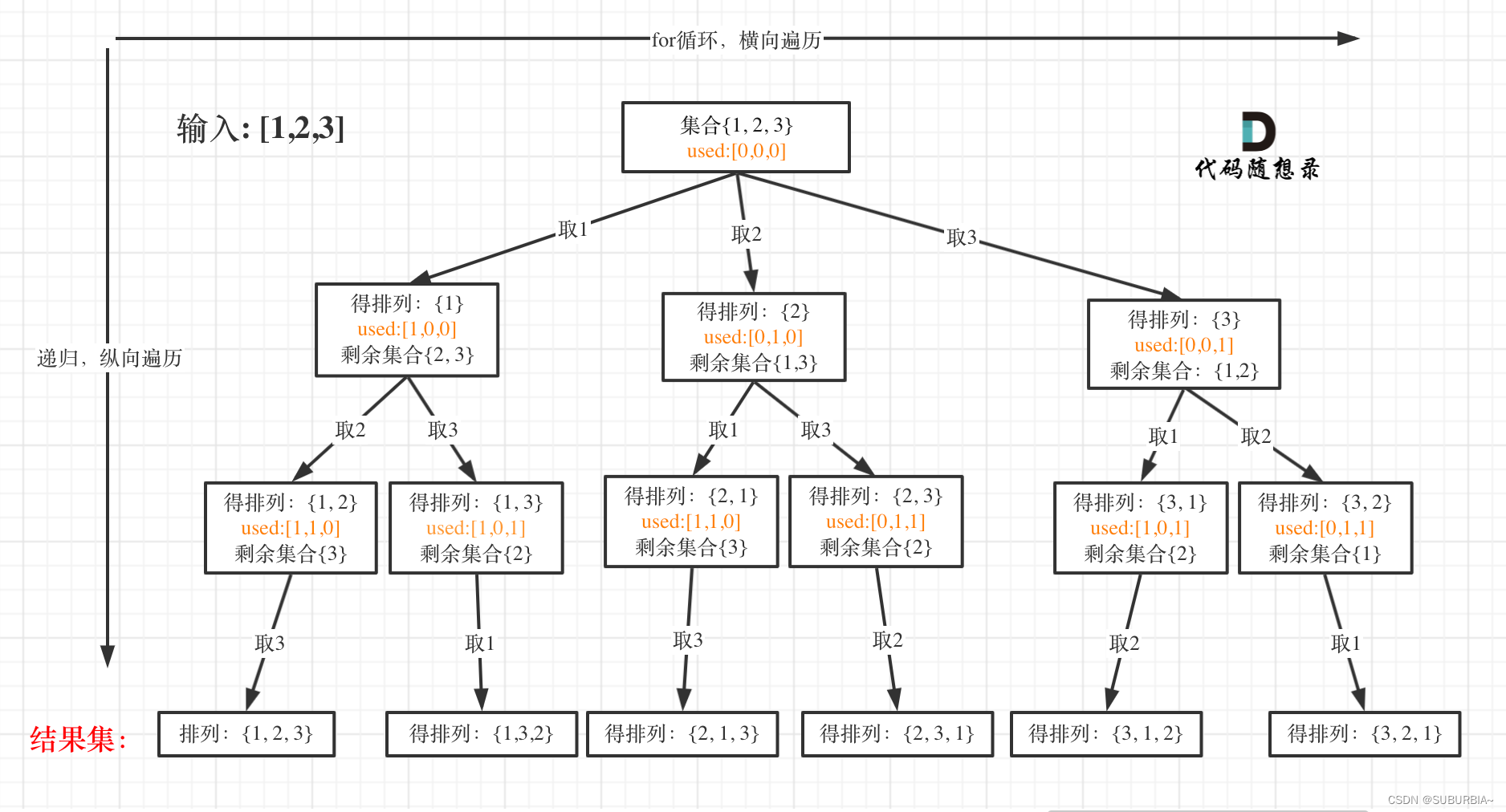
在这里插入图片描述

每层都是从0开始搜索而不是startIndex

需要used数组记录path里都放了哪些元素了

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {if (nums.length == 0) {return result;}used = new boolean[nums.length];backTracking(nums);return result;}private void backTracking(int[] nums) {if (path.size() == nums.length) {result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if (used[i]) {continue;}used[i] = true;path.add(nums[i]);backTracking(nums);path.removeLast();used[i] = false;}}
}

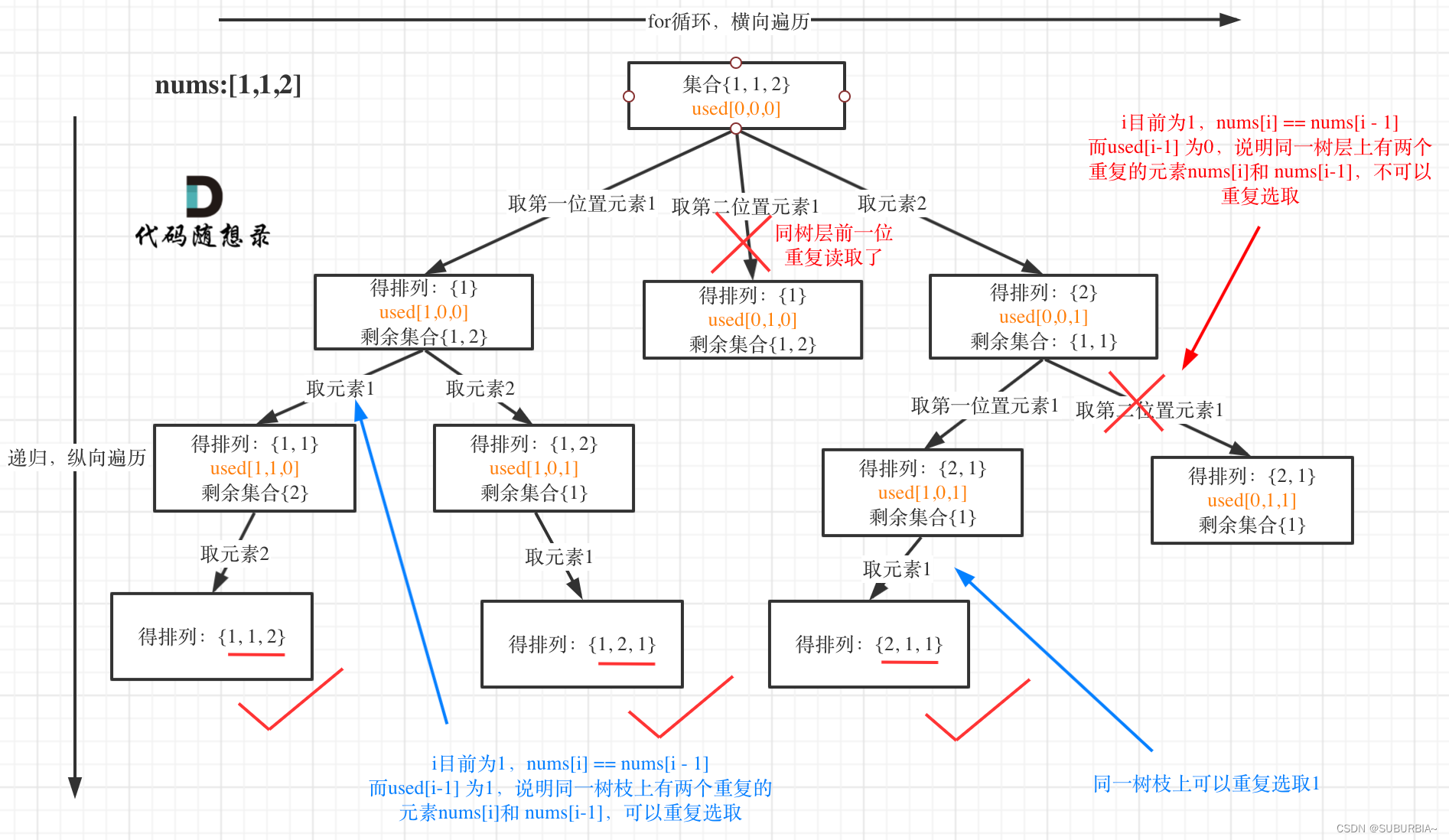
全排列 II

给定一个可包含重复数字的序列，要返回所有不重复的全排列

去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。

组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。
在这里插入图片描述

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();boolean[] used;public List<List<Integer>> permuteUnique(int[] nums) {used = new boolean[nums.length];// 加标志数组，用来辅助判断同层节点是否已经遍历Arrays.fill(used, false);// 为了将重复的数字都放到一起，所以先进行排序Arrays.sort(nums);backTracking(nums);return result;}   private void backTracking(int[] nums) {if (path.size() == nums.length) {result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {// used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过// used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过// 如果同⼀树层nums[i - 1]使⽤过则直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}// 如果同⼀树⽀nums[i]没使⽤过开始处理if (used[i] == false) {used[i] = true;     // 标记同⼀树⽀nums[i]使⽤过，防止同一树枝重复使用path.add(nums[i]);backTracking(nums);path.removeLast(); // 回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复used[i] = false;}}}
}