AcWing 1207 大臣的旅费（树状DP + 注释详解）-编程知识

AcWing 1207 大臣的旅费（树状DP + 注释详解）

[题目概述]

很久以前，T 王国空前繁荣。
为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。
为节省经费，T 国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。
同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。
J 是 T 国重要大臣，他巡查于各大城市之间，体察民情。
所以，从一个城市马不停蹄地到另一个城市成了 J 最常做的事情。
他有一个钱袋，用于存放往来城市间的路费。
聪明的 J 发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关。
具体来说，一段连续的旅途里，第 1 千米的花费为 11，第 2 千米的花费为 12，第 3 千米的花费为 13，…，第 x 千米的花费为 x+10。
也就是说，如果一段旅途的总长度为 1 千米，则刚好需要花费 11，如果一段旅途的总长度为 2 千米，则第 1 千米花费 11，第 2 千米花费 12，一共需要花费 11+12=23。
J 大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入格式

输入的第一行包含一个整数 n，表示包括首都在内的 T 王国的城市数。
城市从 1 开始依次编号，1 号城市为首都。
接下来 n−1 行，描述 T 国的高速路（T 国的高速路一定是 n−1 条）。
每行三个整数 $P_i,Q_i,D_i$ ，表示城市 $P_i$ 和城市 $Q_i$ 之间有一条双向高速路，长度为 $D_i$ 千米。

输出格式

输出一个整数，表示大臣 J 最多花费的路费是多少。

数据范围

$1 ≤ n ≤ 10^5$
$1 ≤ P_i, Q_i ≤ n$ ,
$1 ≤ D_i ≤ 1000$

输入样例：

输出样例：

本题很容易能画出来一个树，让我们求两点之间的最大路费，也就是最大距离，知道最大距离x，那么路费s = 10 * x + x * (1 + x) / 2。
求一个树中两点的最大距离，就是求该树的直径。这里有一个求树的直径的算法
1.从树中任意找一个点x，求出各个点到x的距离 dist[]
2.找到距离x最远的点y，再从y出发找到距离y最远的点，它到y的距离就是树的直径
可以证明一下

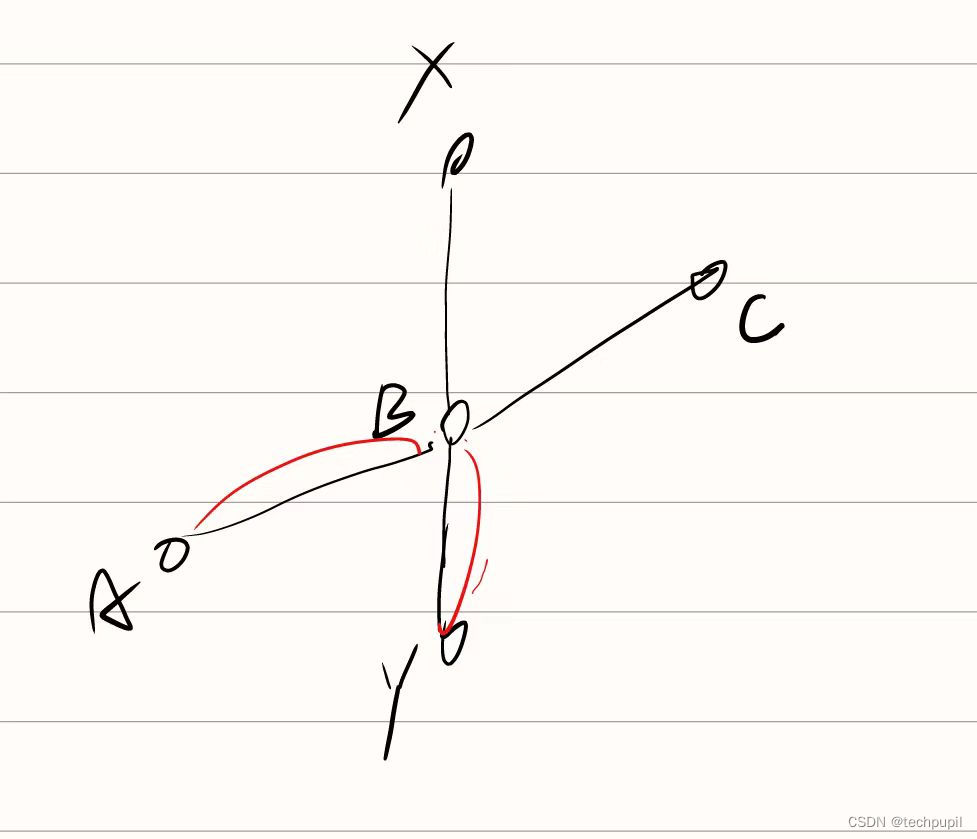
1.xy 和直径有交点，假设y不是直径的端点
ac为直径，y是到x最远的点，那么ax <= xy,所以ab <= by, 所以ac <= cy，那么y一定是直径的端点，和假设矛盾。
2.xy和直径没有交点。
ab为直径，因为每个点中间都是可达的，所有他俩中间必然有一条线穿过。
xy >= xb -> cy >= cb -> dy >= bd -> ay >= ab ，所以y一定是直径的一个端点，与假设矛盾。

完整代码（注释版）

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#define x first
#define y second
using namespace std;const int N = 100005;
int n, a, b, c, dist[N];
// 定义一个结构体存放要去的结点编号和权值
struct Edge {int id, w;
};// 一个vector数组，h[i]中的数据是 编号为i的结点和哪些结点相连
vector<Edge> h[N];
// u为初始结点，father为父节点（为了保证遍历的时候不走回去），distance为到u的距离
void dfs(int u, int father, int distance) {dist[u] = distance;for (auto edge : h[u]) {if (edge.id != father) {dfs(edge.id, u, distance + edge.w);}}
}int main() {cin >> n;for (int i = 0; i < n - 1; i ++) {cin >> a >> b >> c;// a是b的父节点h[a].push_back({b, c});// b是a的父节点h[b].push_back({a, c});}dfs(1, -1, 0);// 找两次int u = 1;for (int i = 1; i <= n; i ++) {if (dist[i] > dist[u])u = i;}dfs(u, -1, 0);for (int i = 1; i <= n; i ++) {if (dist[i] > dist[u]) {u = i;}}// 数据大，可能会爆intlong long s = dist[u];cout << 10 * s + s * (1 + s) / 2 << endl;return 0;
}