目录
🎈了解题意
🎈算法原理
🎈实现代码

🎈了解题意
给定一个大小为 m x n 的矩阵 mat 和一个整数 k,你需要计算一个新的矩阵 answer,其中每个 answer[i][j] 表示矩阵 mat 中以坐标 (i, j) 为中心、边长为 2*k+1 的正方形区域内所有元素的和。
换句话说,对于每个答案元素 ret[i][j],其值是由以 mat[i][j] 为中心、边长为 2*k+1 的正方形区域内的所有元素之和组成的。以每个元素为中心的大小为 (2k+1)*(2k+1) 的子矩阵的元素之和。
mat是一个二维矩阵(三行三列)

k=1的意思是每个下标对应的值向外都扩展1个单位,将扩展1个单位后包含的所有数字都加起来,就是最终的结果(还是该下标)
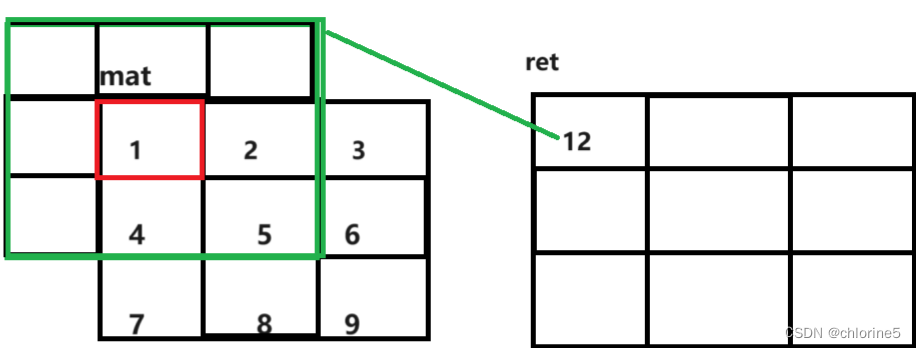
就像图中所展现的一样,1的位置开始向外扩展k个单位,就是绿色包围的地方,超过的范围区域不记,剩下的是2,4,5,1(这里需要加上1),相加的结果是12,所以ret结果数组的第一行第一列的数字是12.
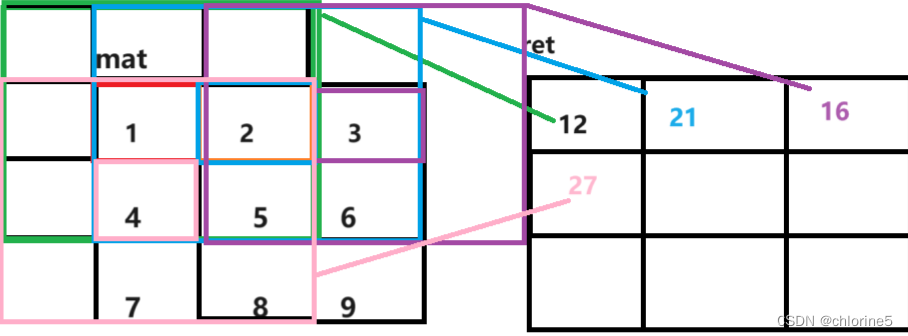
按照这种方法我们依次扩展k个单位,再依次相加就得到ret数组。
🎈算法原理
我们首先需要预处理一个前缀和,将每个子区间的前缀和进行计算,但是我们需要知道,上一篇的二维前缀和是从1开始,而我们这一题是从0开始的,但是我们预处理前缀和依旧是设定m+1行n+1列,初始化为0.
i和j都是从1开始的。
dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i-1][j-1]-dp[i-1][j-1];
本题都是从1开始的,所以我们要减去加上那个数,需要将i,j都减1,我们打个比方我们要加上 下标[0][20],但是本题是从1开始,那么对应的i=1 j=1,我们要加上对应的值的话,我们需要将i-1,j-1.否则会导致结果不对。
这行代码声明了一个名为 dp 的二维 vector,其大小为 (m+1) x (n+1)。其中,dp[i][j] 表示矩阵中以 (i, j) 为右下角顶点的子矩阵的和。这样的声明方式初始化了一个大小为 (m+1) x (n+1) 的二维 vector,并将其中的每个元素初始化为 0。
然后我们来使用前缀和,我们需要的区间在横坐标的区间是i-k到i+k,纵坐标是j-k到j+k

如果我们出现了下面的情况呢?
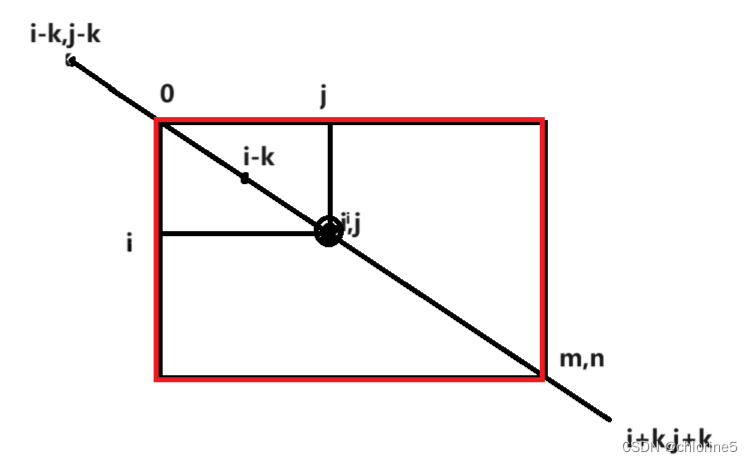
我们看到(i-k,j-k)越过了0,又或者(i+k,j+k)越过了(m,n),所以我们要在(i-k,j-k)(0,0)取大值,在(i+k,j+k),(m,n)取小值,我们要防止越界情况。
注意,如果正方形区域的边界超出了矩阵的边界,则超出的部分将被视为 0 处理。
x1=i-k max(0,i-k) +1 x2=i+k min(i+k,m)+1
y1=j-k max(0,j-k) +1 y2=j+k min(j+k,n)+1
求(x1,y1)到(x2,y2)区间的前缀和
这里为什么+1呢?dp代表前缀和,他是从1开始的,那么如果我们要算某个特定区间的前缀和,我们需要将区间+1,因为本题的mat数组下标从0开始。
最后我们就使用得出特定区间的前缀和
ret数组依旧是m行n列的初始化为0。
ret[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];
🎈实现代码
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m=mat.size(),n=mat[0].size();//1.预处理一个前缀和矩阵vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];}}//使用vector<vector<int>> ret(m,vector<int>(n));for(int i=0;i<m;i++){for(int j=0;j<n;j++){int x1=max(0,i-k)+1,y1=max(0,j-k)+1;int x2=min(m-1,i+k)+1,y2=min(n-1,j+k)+1;ret[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];}}return ret;}
};慢,不妨再慢点。