图的存储：
1.邻接矩阵：
我们用map[i][j]表示i--->j的边权
2.用vector数组（在搜索专题的游戏一题中应用过）
3.用邻接表：
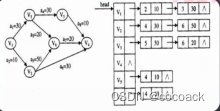下面是用链表实现的基本功能的代码：
#include<bits/stdc++.h>
using namespace std;
struct node{int dian,zhi;struct node* next;
};
void insert(int x,int y,int z){node *p=new node;p->dian=y;p->zhi=z;p->next=head[x];head[x]=p;
}4.用伪邻接表（链式前向星）（注意第一个next=-1，开始直接memset head=-1即可)
对于（1，3，30,-1）表示1的点指向3，边权为30,下一条边.
我们把这个存在edge[1]里，并令head[1]=1;
(3,6,10，-1),我们存在edge[2]里，并令head[3]=2;
(1,2,10，head[1])，我们存在edge【3】里，并让head[1]=3;
下面是实现的代码：
#include<bits/stdc++.h>
using namespace std;
struct node{int dian,zhi;int next;
};
void insert(int x,int y,int z){edge[++m].dian=y;edge[m].zhi=z;edge[m].next=head[x];head[x]=m;
}欧拉图（前提是联通）
如果图的一个路径包括每个边恰好一次，则为欧拉路径。
欧拉路径+回路=欧拉回路。
具有欧拉回路的图为欧拉图，具有欧拉路径但无欧拉回路的图为半欧拉图
那么如何判断是否为欧拉图呢？
对于无向图，等价于该图所有顶点的度数为偶数（一进一出）+联通。
对于有向图，等价于该图所有顶点的入度==出度+联通。
拓扑排序
即按照一定的规则安排活动的先后次序（可能有多解）。
现在给一张图，a--》b表示要完成b必须先完成a，那我们如何排序呢？
1.先找没有前驱的点作为开始。
2.把它连着的边给删除，产生更多没有前驱的点作为下一步，入度-1。
3.删不动则无法完成。
具体实现中，我们不能总是去跑入度为0的点。
于是，我们用一个队列。在删后发现入度为0的点就放入队列中即可。
下面是实现的代码：
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt;
struct node{int dian;int next;
}edge[1000000];
int head[1010],inc[1010];
queue<int> q;
void insert(int x,int y){edge[++cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
void tuopu(){for(int i=1;i<=n;i++){if(inc[i]==0) q.push(i);}int tot=0;while(!q.empty()){int x=q.front();q.pop();cout<<x<<endl;tot++;for(int i=head[x];i!=-1;i=edge[i].next){inc[edge[i].dian]--;if(inc[edge[i].dian]==0){q.push(edge[i].dian);}}}if(tot!=n) cout<<-1;
}
int main(){cin>>n>>m;memset(head,-1,sizeof(head));for(int i=1;i<=m;i++){int x,y;cin>>x>>y;insert(x,y);inc[y]++;}tuopu();
}拓扑排序的应用：
1.判断一个有向图是否有环，无环的图所有点都可以拓扑排序。
2.AOE网：
对于第一个，我们只用在拓扑排序上维护时间的max即可。
对于第二个，我们可以计算一下每一个活动的最早开始时间与最晚开始时间，因此我们相当于求最早开始时间等于最晚开始时间的点。
那么，我们如何求最晚开始时间呢？
我们只要从结尾反方向跑一回即可。
下面是AC代码：
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt;
struct node{int dian;int next;int zhi;
}edge[1000000];
int head[1010],inc[1010],shijian[1010];
queue<int> q;
void insert(int x,int y,int z){edge[++cnt].dian=y;edge[cnt].next=head[x];edge[cnt].zhi=z;head[x]=cnt;
}
void tuopu(){for(int i=1;i<=n;i++){if(inc[i]==0){q.push(i);shijian[i]=0;}}while(!q.empty()){int x=q.front();q.pop();for(int i=head[x];i!=-1;i=edge[i].next){inc[edge[i].dian]--;shijian[edge[i].dian]=max(shijian[edge[i].dian],shijian[x]+edge[i].zhi);if(inc[edge[i].dian]==0){q.push(edge[i].dian);}}}
}
int main(){cin>>n>>m;memset(head,-1,sizeof(head));for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y>>z;insert(x,y,z);inc[y]++;}tuopu();cout<<shijian[n];
}
