基于3Blue1Brown视频的笔记
一种新的看待方式
对于一个向量,比如说,如何看待其中的3和-2?
一开始,我们往往将其看作长度(从向量的首走到尾部,分别在x和y上走的长度)。
在有了数乘后,我们可以将其视为对向量进行缩放的标量,缩放的对象是两个特殊的向量 和
,这两个向量也被称为xy坐标系的基向量。
也就是有:
这种把向量看作向量的数乘的和的思想正体现了数乘和相加是线性代数的核心。

这里很自然引出一个问题,可不可以换另外的向量作基向量?
比如这里我们用 和
,想象一下任意缩放这两个向量,然后相加,得到不同的结果。
感性上,我们可以得到所有二维平面中的向量;实际上,确实如此。
具体为什么,以及在这样的基下,坐标和向量的关系,可以暂且往后放。目前需要认识到的是,每当我们用数字描述向量时,它都依赖于我们正在使用的基。
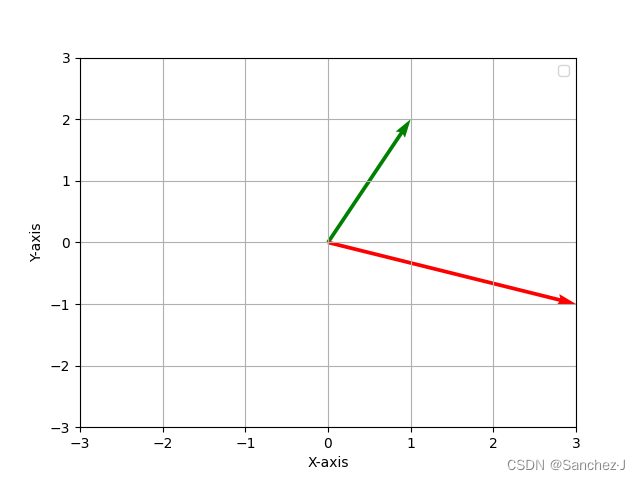
线性组合
两个数乘向量的和被称为这两个向量的线性组合。在xy坐标系,任意取两个向量进行线性组合时,组合出的所有向量实际上有3种情况:
- 两个向量都是零向量时,只能得到零向量。
- 两个向量恰好在一条直线上时,得到的向量终点也全在这条直线上。
- 其余情况,能得到整个平面所有向量。
张成的空间
这里又引入一点术语:
所有可以表示为给定向量线性组合的向量的集合,称为给定向量张成的空间。
所以,对于大多数二维向量来说,它们张成的空间是整个二维平面的向量;但当共线时,它们张成的空间就是终点落在一条直线上的向量的集合。
我们可以总结,张成的空间实际上就是在问:仅仅通过向量加法与向量数乘这两种基础运算,能获得的所有向量的集合是什么?
向量与点
由于在线性代数中,向量的起点总是在原点,因此可以直接用终点坐标来表示向量,即用点来表示向量。
线性相关/无关
在三维坐标系中,先取两个不共线的向量,两者张成以一个平面,然后再取一个向量,如果没有落在这个平面,那么三者的线性组合可以得到整个三维空间的所有向量。
而当这第3个向量恰好落在前两个向量张成的平面里时,三者张成的空间没有变化,至少有一个向量对张成的空间没有贡献,可以删去而不减小张成的空间,这种情况称它们是线性相关的前面两个向量共线的情况也是如此。
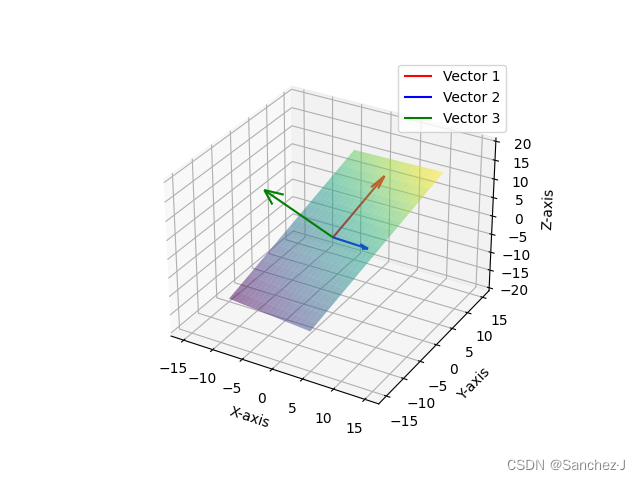
另一种对于线性相关等效的描述是:其中一个向量能被其他向量的线性组合表示(因为这个向量已经落在它们张成的空间中了)
而如果每一个向量都不是多余的,都给张成的空间增添了新的维度,那么我们称它们线性无关
基
基(basis)是什么在前文已经提到过了,其严格定义是:
向量空间的一组基是张成该空间的一个线性无关的向量集