坚持刷题｜重建二叉树-编程知识

文章目录

题目
考察点
代码实现
实现总结
扩展问题
- 从前序和中序遍历中序列构建二叉树
- - 题目
  - 代码实现
  - 与后序实现的异同点
- 前序和后序可不可以唯一确定一棵二叉树呢？

Hello，大家好，我是阿月。坚持刷题，老年痴呆追不上我，今天刷：重建二叉树

题目

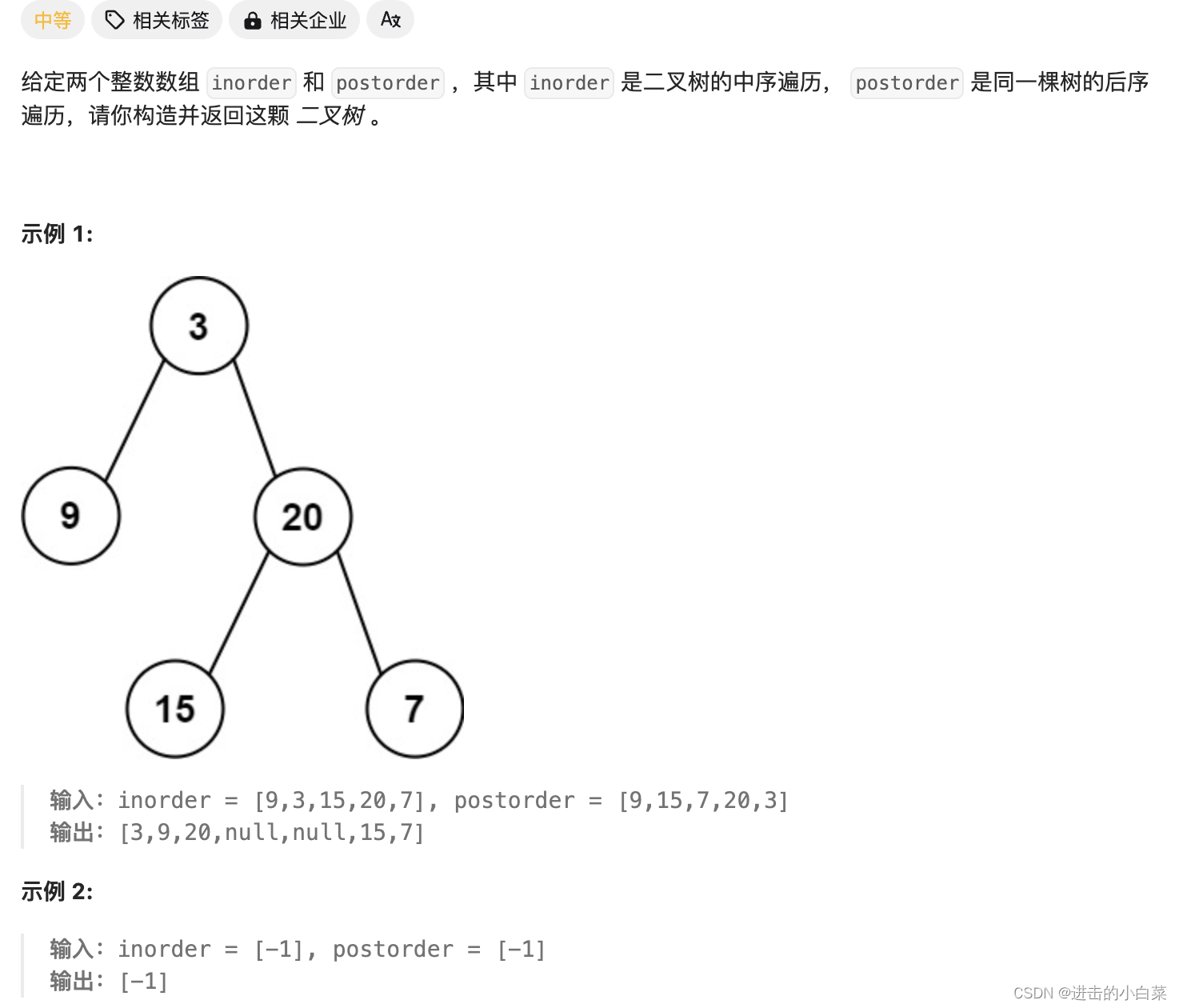
106. 从中序与后序遍历序列构造二叉树
在这里插入图片描述

考察点

不仅考察了对数据结构和算法的理解，还考察了如何将理论知识转化为实际的代码实现，并且需要考虑算法的效率和优化：

二叉树的遍历：需要理解中序遍历和后序遍历的概念，并知道它们的应用场景和特点。
递归：在构造二叉树的过程中，需要使用递归算法来处理子树。
数组操作：需要熟练地对数组进行索引和切片操作，以便在中序和后序遍历序列中定位根节点和子树的范围。
二叉树的构造：理解如何根据中序遍历和后序遍历序列构造二叉树，包括根据根节点在中序遍历中的位置将树分割成左右子树，并且根据后序遍历序列确定左右子树的范围。
时间复杂度分析：在实现算法时需要考虑其时间复杂度，尤其是递归算法的时间复杂度分析，以确保算法的效率。

代码实现

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {if (inorder == null || postorder == null || inorder.length != postorder.length) {return null;}return buildTreeHelper(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);}private TreeNode buildTreeHelper(int[] inorder, int inStart, int inEnd,int[] postorder, int postStart, int postEnd) {if (inStart > inEnd || postStart > postEnd) {return null;}int rootValue = postorder[postEnd];TreeNode root = new TreeNode(rootValue);int rootIndex = 0;for (int i = inStart; i <= inEnd; i++) {if (inorder[i] == rootValue) {rootIndex = i;break;}}int leftTreeSize = rootIndex - inStart;root.left = buildTreeHelper(inorder, inStart, rootIndex - 1,postorder, postStart, postStart + leftTreeSize - 1);root.right = buildTreeHelper(inorder, rootIndex + 1, inEnd,postorder, postStart + leftTreeSize, postEnd - 1);return root;}public static void main(String[] args) {Solution solution = new Solution();int[] inorder = {9, 3, 15, 20, 7};int[] postorder = {9, 15, 7, 20, 3};TreeNode root = solution.buildTree(inorder, postorder);// 在这里可以添加遍历树的代码来验证结果}
}

实现总结

首先通过后序遍历的最后一个节点找到根节点的值，然后根据中序遍历序列将其分割成左子树和右子树，接着根据后序遍历序列确定左子树和右子树的范围，最后递归构造左子树和右子树即可。
时间复杂度
递归
- 递归函数返回值以及参数：
  - 返回值：重建好的二叉树。
  - 参数：中序遍历序列，中序的开始坐标，中序的结束坐标，后序遍历序列，后序的开始坐标，后序的结束坐标。
- 终止条件：
  - 如果中序遍历或者后序遍历的开始坐标大于结束坐标（inStart > inEnd || postStart > postEnd），也就是数组大小为零，说明是空节点，直接返回。
- 单层递归逻辑：
  - 通过后序遍历找到根节点的值。
  - 根据根节点的值将中序遍历分割为左子树和右子树。
  - 根绝中序遍历切割的左子树和右子树size对后序遍历进行左右子树范围切割。
时间复杂度：O(n^2)。
- 首先，在每个节点的递归调用中，需要在中序遍历序列中搜索根节点的位置。这个操作的时间复杂度是 O(n)，因为在最坏的情况下，可能需要遍历整个中序遍历序列来找到根节点的位置。
- 然后，对每个节点都会进行递归操作。在最坏情况下，每个节点都需要处理一次，因此总的时间复杂度是 O(n)。
- 总体来说，这个算法的时间复杂度是 O(n^2)。

扩展问题

从前序和中序遍历中序列构建二叉树

题目

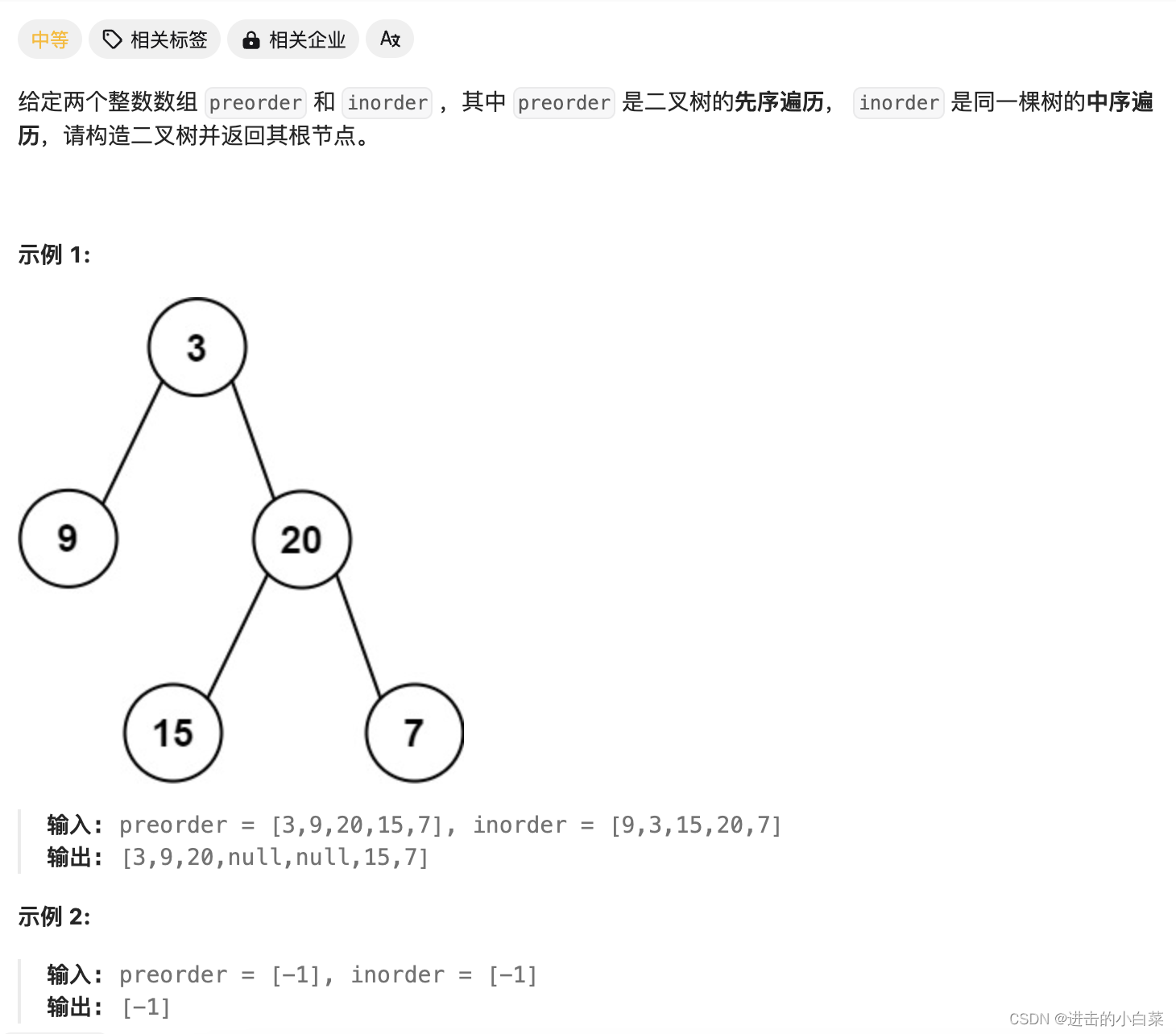
105. 从前序与中序遍历序列构造二叉树
在这里插入图片描述

代码实现

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {if (preorder == null || inorder == null || preorder.length != inorder.length) {return null;}return buildTreeHelper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);}private TreeNode buildTreeHelper(int[] preorder, int preStart, int preEnd,int[] inorder, int inStart, int inEnd) {if (preStart > preEnd || inStart > inEnd) {return null;}int rootValue = preorder[preStart];TreeNode root = new TreeNode(rootValue);int rootIndex = 0;for (int i = inStart; i <= inEnd; i++) {if (inorder[i] == rootValue) {rootIndex = i;break;}}int leftTreeSize = rootIndex - inStart;root.left = buildTreeHelper(preorder, preStart + 1, preStart + leftTreeSize,inorder, inStart, rootIndex - 1);root.right = buildTreeHelper(preorder, preStart + leftTreeSize + 1, preEnd,inorder, rootIndex + 1, inEnd);return root;}public static void main(String[] args) {Solution solution = new Solution();int[] preorder = {3, 9, 20, 15, 7};int[] inorder = {9, 3, 15, 20, 7};TreeNode root = solution.buildTree(preorder, inorder);// 在这里可以添加遍历树的代码来验证结果}
}

与后序实现的异同点

异：
- 根节点的确定：
  - 在前序遍历中，根节点总是序列的第一个元素。
  - 在后序遍历中，根节点总是序列的最后一个元素。
- 子树的顺序划分：
  - 在前序遍历中，左子树的元素紧随着根节点之后，而右子树的元素在左子树元素之后，具有明显的顺序。
  - 在后序遍历中，右子树的元素位于根节点之前，而左子树的元素位于右子树之前，同样具有明显的顺序。
同：
- 从前序和中序遍历序列构建二叉树的递归过程和从后序和中序遍历序列构建二叉树的递归过程在本质上是相似的。