毕达哥拉斯定理

毕达哥拉斯的著名定理所讲的是，假设一直角三角形的三边长为a、b和c，其中c是斜边长（直角所对的边），则 $a^2+b^2=c^2$。这个定理有若干种证明，其中有一种特别简短，而且很容易理解。
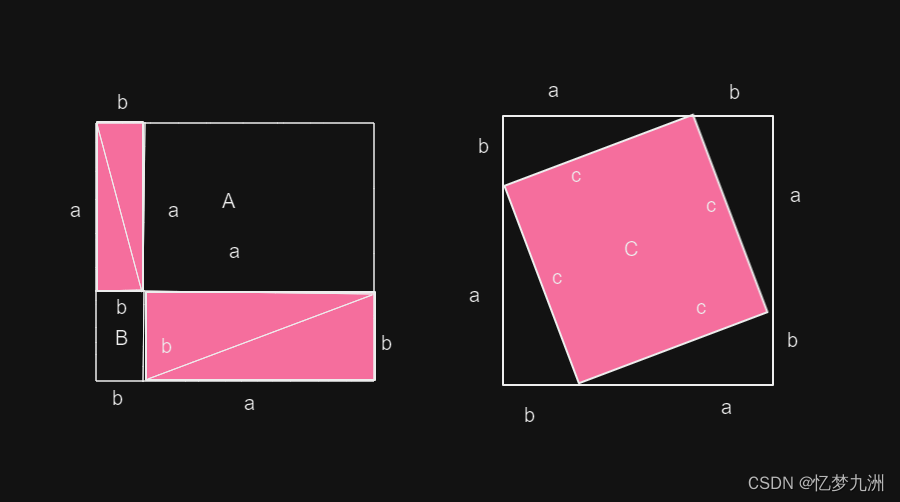
它差不多只需要下面两幅图即可。

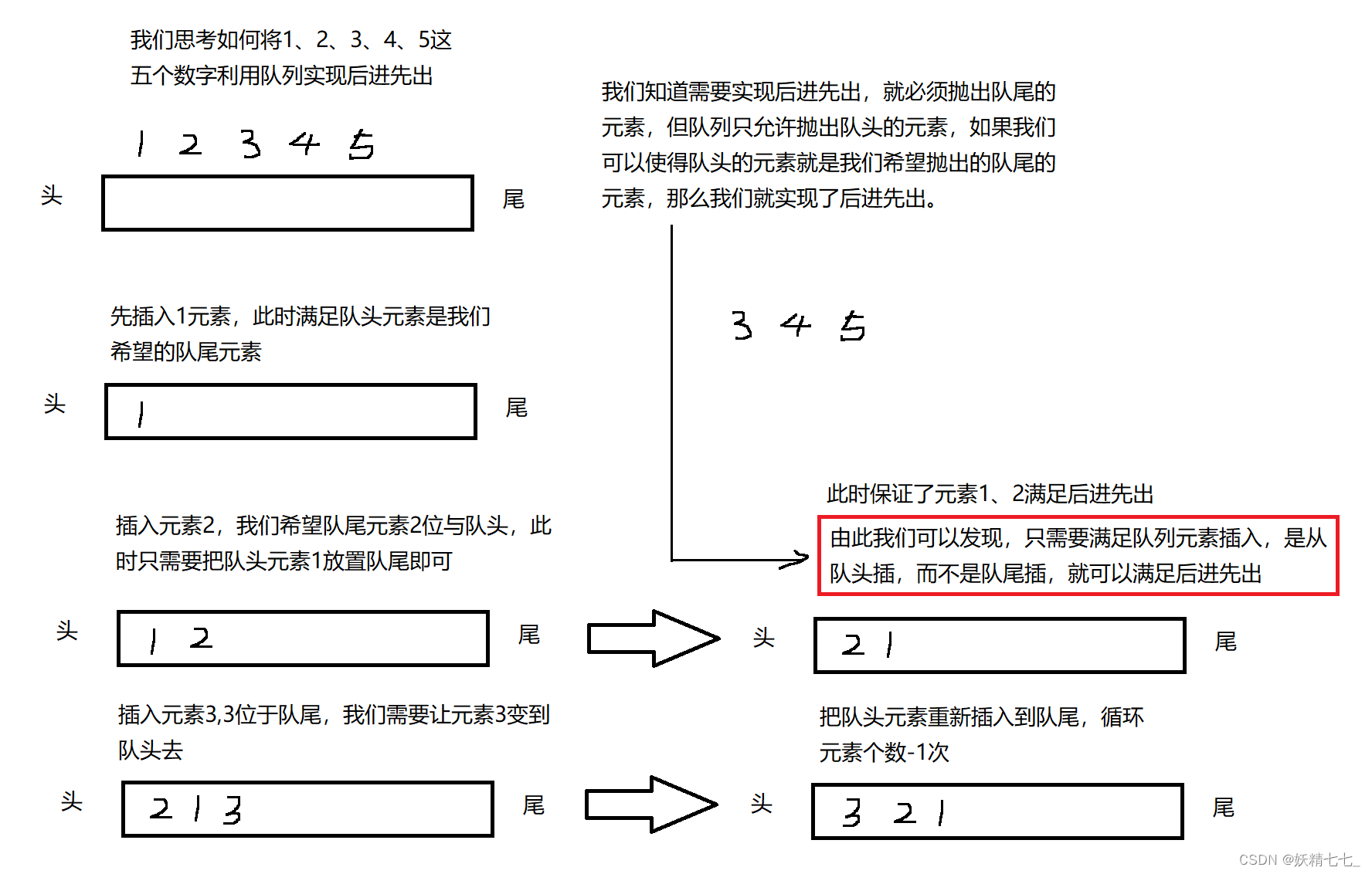
“面积之谜：图形变换的思考引发的面积差异”

上图中，我标为A、B、C的正方形，边长分别为a、b、c，因而面积分别为$a^2、b^2、c^2$。因为四个三角形的移动并没有引发面积的改变，也没有使它们重合，所以两幅图中，大正方形去掉四个小三角形所得的面积应当是相同的。但在左图中，这个面积是$a^2+b^2$，而右图中则是$c^2$。

总结

在毕达哥拉斯定理中，我们探讨了直角三角形的性质。这一定理指出，对于一个直角三角形，其两个直角边的平方和等于斜边的平方。这个定理有许多不同的证明方法，其中一种特别简洁且易于理解。
通过观察两幅图形，我们可以发现一个有趣的现象。在两个等面积的正方形中，分别标记为A、B、C，它们的边长分别为a、b、c，对应的面积分别为$a^2、b^2、c^2$。由于四个三角形的移动并不改变面积，也不使它们重叠，所以在两幅图中，去掉四个小三角形所得的面积应该是相同的。然而，在左图中，这个面积是$a^2+b^2$，而在右图中则是$c^2$。
这个观察引发了对面积之谜的思考，同时也与毕达哥拉斯定理的形式相呼应。毕达哥拉斯定理通过数学的严谨证明，揭示了直角三角形边长之间的关系。这个定理在几何学和应用数学中具有广泛的应用。通过对图形变换的思考，我们不仅更好地理解了毕达哥拉斯定理，还发现了面积差异的有趣现象。这个过程展示了数学中对形状和关系的深入思考与探索的重要性。