一、最长公共扩展（LCE）问题

考虑一个字符串s，并为每对（L，R）计算从L和R开始的s的最长子字符串。
在LCE中，在每个查询中，我们必须回答从索引L和R开始的最长公共前缀的长度。

例子：

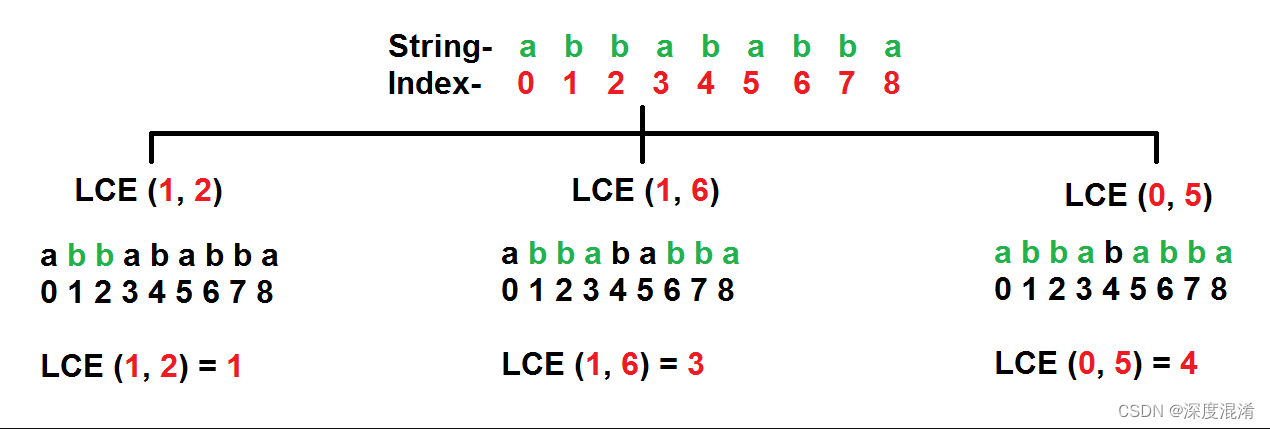
字符串：abbababba

查询：LCE（1,2）、LCE（1,6）和LCE（0,5）

求从索引（1,2）、（1,6）和（0,5）开始的最长公共前缀的长度。

突出显示的字符串“绿色”是从相应查询的索引-L和R开始的最长公共前缀。

我们必须找到从索引-（1，2），（1，6）和（0，5）开始的最长公共前缀的长度。

二、LCE的算法（朴素方法）

1、对于表格-LCE（L，R）中的每个LCE查询，请执行以下操作：

（1）将LCE“长度”初始化为0

（2）开始逐个字符比较从索引-L和R开始的前缀。

（3）如果字符匹配，那么这个字符在我们最长的公共扩展名中。所以增加“长度”（length++）。

（4）否则，如果字符不匹配，则返回此“长度”。

2、返回的“长度”将是所需的LCE（L，R）。

三、源程序

1、原始（Native）算法 

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public class LCE_Query{/// <summary>/// 开始位置（下标）/// </summary>public int Left { get; set; } = 0;/// <summary>/// 结束位置（下标）/// </summary>public int Right { get; set; } = 0;/// <summary>/// 构造函数/// </summary>/// <param name="left"></param>/// <param name="right"></param>public LCE_Query(int left, int right){this.Left = left;this.Right = right;}}public static partial class LCE_Computation{public static int LCE(string str, int n, int left, int right){int length = 0;while ((right + length) < n && str[left + length] == str[right + length]){length++;}return (length);}public static List<string> LCEQueries(string str, int n, LCE_Query[] q, int m){List<string> vs = new List<string>();for (int i = 0; i < m; i++){int left = q[i].Left;int right = q[i].Right;vs.Add("LCE (" + left + ", " + right + ") = " + LCE(str, n, left, right));}return vs;}}
}

2、RMQ（Range Minimum Query）算法

RMQ（Range Minimum Query）算法，也称为 DMA（Direct Minimum Algorithm）算法。

其中使用凯撒（Kasai）算法从后缀数组中找到 LCP 数组。

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public class Suffix : IComparable{/// <summary>/// original index/// </summary>public int index { get; set; } = 0;/// <summary>/// ranks and next rank pair/// </summary>public int[] rank = new int[2];public int CompareTo(object obj){Suffix b = obj as Suffix;if (this.rank[0] == b.rank[0] && this.rank[1] == b.rank[1]) return 1;return -1;//return ((this.rank[0] == b.rank[0]) ?//			(this.rank[1] < b.rank[1]) ://			(this.rank[0] < b.rank[0])) ? 1 : -1;}}/// <summary>/// 最长公共扩展/// Find the length of longest common extension/// using Direct Minimum Algorithm/// </summary>public class LCE_Direct_Minimum_Algorithm{private List<int> Build_Suffix_Array(string txt, int n){Suffix[] suffixes = new Suffix[n];for (int i = 0; i < n; i++){suffixes[i].index = i;suffixes[i].rank[0] = txt[i] - 'a';suffixes[i].rank[1] = ((i + 1) < n) ? (txt[i + 1] - 'a') : -1;}Array.Sort(suffixes);int[] ind = new int[n];for (int k = 4; k < 2 * n; k = k * 2){int rank = 0;int prev_rank = suffixes[0].rank[0];suffixes[0].rank[0] = rank;ind[suffixes[0].index] = 0;for (int i = 1; i < n; i++){if (suffixes[i].rank[0] == prev_rank && suffixes[i].rank[1] == suffixes[i - 1].rank[1]){prev_rank = suffixes[i].rank[0];suffixes[i].rank[0] = rank;}else{prev_rank = suffixes[i].rank[0];suffixes[i].rank[0] = ++rank;}ind[suffixes[i].index] = i;}for (int i = 0; i < n; i++){int nextindex = suffixes[i].index + k / 2;suffixes[i].rank[1] = (nextindex < n) ? suffixes[ind[nextindex]].rank[0] : -1;}Array.Sort(suffixes);}List<int> suffixArr = new List<int>();for (int i = 0; i < n; i++){suffixArr.Add(suffixes[i].index);}return suffixArr;}private List<int> Kasai(string txt, List<int> suffixArr, ref List<int> invSuff){int n = suffixArr.Count;List<int> lcp = new List<int>(n);for (int i = 0; i < n; i++){invSuff[suffixArr[i]] = i;}int k = 0;for (int i = 0; i < n; i++){if (invSuff[i] == n - 1){k = 0;continue;}int j = suffixArr[invSuff[i] + 1];while (i + k < n && j + k < n && txt[i + k] == txt[j + k]){k++;}lcp[invSuff[i]] = k;if (k > 0){k--;}}return lcp;}private int LCE(List<int> lcp, List<int> invSuff, int n, int L, int R){if (L == R){return (n - L);}int low = Math.Min(invSuff[L], invSuff[R]);int high = Math.Max(invSuff[L], invSuff[R]);int length = lcp[low];for (int i = low + 1; i < high; i++){if (lcp[i] < length){length = lcp[i];}}return (length);}public List<string> LCEQueries(string str, int n, LCE_Query[] q, int m){List<int> suffixArr = Build_Suffix_Array(str, str.Length);List<int> invSuff = new List<int>(n);List<int> lcp = Kasai(str, suffixArr, ref invSuff);List<string> result = new List<string>();for (int i = 0; i < m; i++){int L = q[i].Left;int R = q[i].Right;result.Add(String.Format("LCE ({0}, {1}) = {2}", L, R, LCE(lcp, invSuff, n, L, R)));}return result;}}
}

——————————————————————————

POWER BY  TRUFFER.CN