目录

递归算法原理

力扣面试题 08.06. 汉诺塔问题

解析代码

---

递归算法原理

        递归算法个人经验：给定一个任务，相信递归函数一定能解决这个任务，根据任务所需的东西，给出函数参数，然后实现函数内容，最后找出口。

        递归算法是指在解决问题的过程中，不断地调用自身来解决子问题的一种算法。其基本思想是将原问题转化为同类更小的子问题，直到达到最小可解问题的情况，然后再将子问题的答案合并起来解决原问题。递归算法基本设计原理是分而治之，即将问题分成小问题分别解决，最终将所有小问题的答案合并成原问题的答案。

        递归算法适用于问题具有递归性质的场景。这些问题通常可以分解为一些同样类型但规模更小的子问题，递归算法可以通过递归调用来解决这些子问题，再将子问题的答案组合成原问题的答案。例如，计算斐波那契数列，求解汉诺塔问题等等都可以用递归算法来解决。

        在使用递归算法中，首先要注意递归终止条件的设置。如果没有正确的终止条件，递归算法将会无限循环，导致程序崩溃。其次，注意递归调用时的参数传递问题，要确保每次递归调用时传递的参数和问题规模正确。此外，在递归算法中，可能会出现栈溢出的问题，特别是问题规模很大的情况下，应注意算法的时间和空间复杂度，以避免因内存不足而引起的程序异常。

递归 VS 迭代（循环）：

递归和迭代本质都是解决重复的子问题，所以代码可以相互转换。

递归 VS 深搜（dfs）：

递归的展开图，其实就是对一颗树做一次深度优先遍历。

什么时候用递归方便，什么时候用迭代方便：

当递归展开图复杂时用递归（多叉树等），当递归展开图简单时用迭代（一条路径等）。

---

力扣面试题 08.06. 汉诺塔问题

面试题 08.06. 汉诺塔问题

难度 简单

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例1:

 输入：A = [2, 1, 0], B = [], C = []
 输出：C = [2, 1, 0]

示例2:

 输入：A = [1, 0], B = [], C = []
 输出：C = [1, 0]

提示:

1. A中盘子的数目不大于14个。

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {};

---

解析代码

一道递归方法的经典题目，看看图：

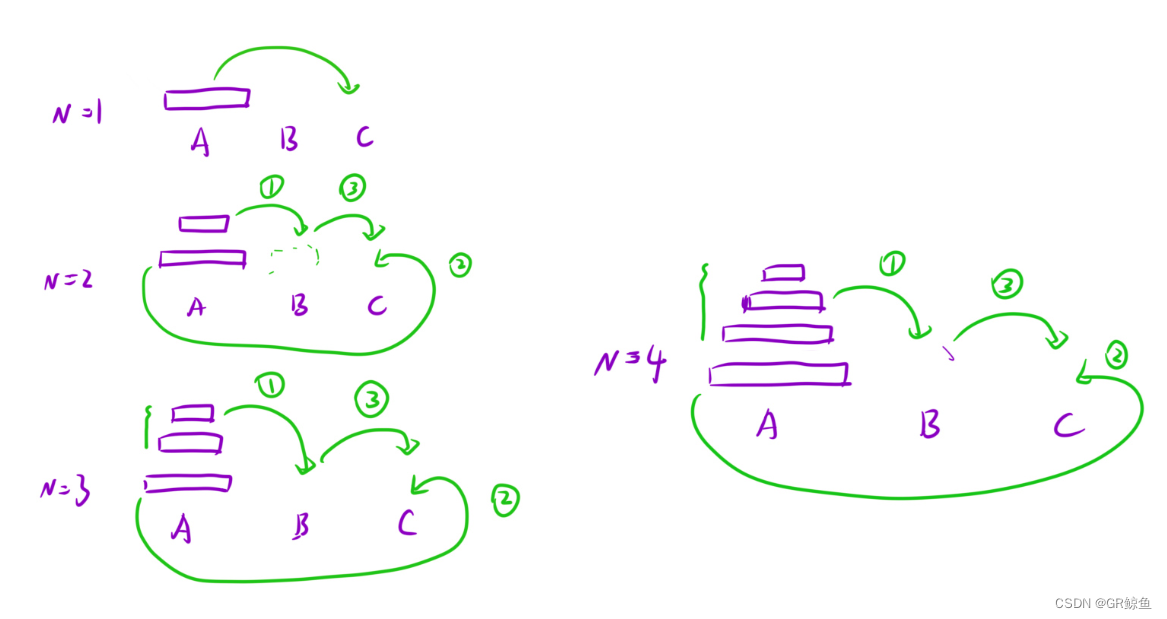
假设 n = 1,只有一个盘子，很简单，直接把它从 A 中拿出来，移到 C 上；

如果 n = 2 呢？这时候我们就要借助 B 了，因为小盘子必须时刻都在大盘子上面，共需要 4 步。

如果 n > 2 呢？思路和上面是一样的，我们把 n 个盘子也看成两个部分，一部分有 1 个盘子，另一部分有 n - 1 个盘子。

        在思考这个问题的时候，就将最初的 n 个盘子从 A 移到 C 的问题，转化成了将 n - 1 个盘子从 A 移到 C 的问题， 依次类推，直至转化成 1 个盘子的问题时，问题也就解决了。这就是分治的思想。

        而实现分治思想的常用方法就是递归。不难发现，如果原问题可以分解成若干个与原问题结构相同但规模较小的子问题时，往往可以用递归的方法解决。具体解决办法如下：

n = 1 时，直接把盘子从 A 移到 C；
n > 1 时，
先把上面 n - 1 个盘子从 A 移到 B（子问题，递归）；
再将最大的盘子从 A 移到 C；
再将 B 上 n - 1 个盘子从 B 移到 C（子问题，递归）。

递归法：给定一个任务，相信递归一定能解决这个任务，然后写函数体和找出口。

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A, B, C, A.size());}void dfs(vector<int>& A, vector<int>& B, vector<int>& C, int n){   // 递归：A盘 借助 B盘 转移A最上面n-1个盘 到C盘if(n == 1){C.push_back(A.back());A.pop_back();return;}dfs(A, C, B, n-1);C.push_back(A.back());A.pop_back();dfs(B, A, C, n-1);}
};