组合总和

class Solution{
private:vector<vector<int>>result;vector<int>path;void backtracking(vector<int>& candidates,int target,int sum,int startIndex){if(sum > target){return;}if(sum == target){result.push_back(path);return;}for(int i = startIndex; i < candidates.size(); i++){sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates,target,sum,i);sum -= candidates[i];path.pop_back();}}public:vector<vector<int>>combinationSum(vector<int>&candidates, int target){result.clear();path.clear();backtracking(candidates,target,0,0);return result;}
};

剪枝（优化）

 先排序，才能剪枝,在for循环处剪枝

class Solution{
private:vector<vector<int>>result;vector<int>path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex){if(sum == target){result.push_back(path);return;}for(int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++){sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates,target,sum,i);sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>>combinationSum(vector<int>&candidates,int target){result.clear();path.clear();sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,0);return result;}
};

组合总和II

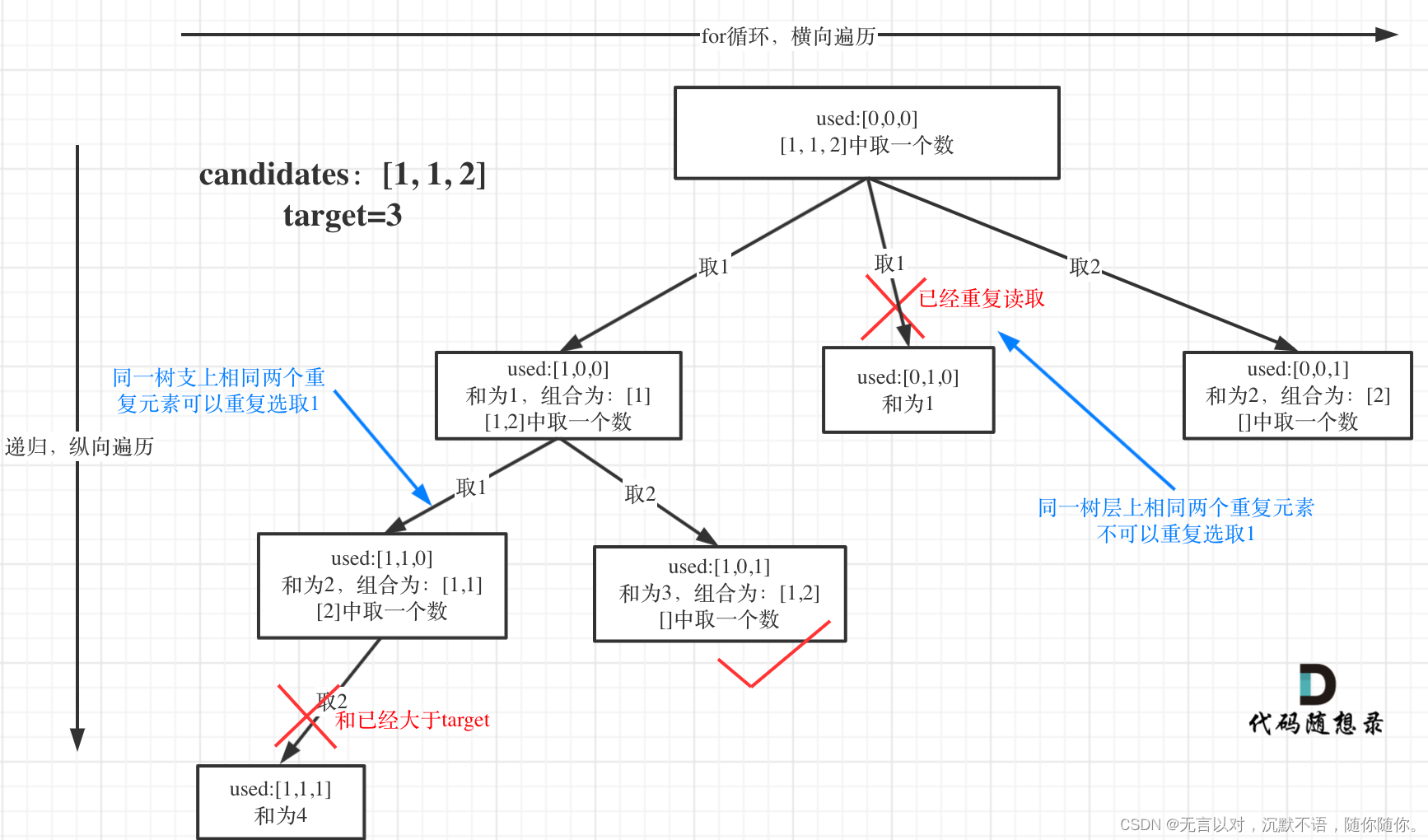
题目：给定数组candidates和一个目标数target，找出candidates中所有可以使数字和target的组合。candidates中的每个数字在每个组合中只能使用一次。 解集中不包含重复的组合。

思路：先用前面学的回溯算法，求出解集合，再用set或map去重。缺点：麻烦，易超时。

优解：在搜索中直接去重。（使用过的元素不再使用）

树层去重，树枝去重

树层，横向避免重复，先排序，相同的挨着，前面遍历过，就不用再遍历了。

树枝可以，纵向是一个组合内的元素，可以重复。

class Solution{
private:vector<vector<int>>result;vector<int>path;
void backtracking(vector<int>& candidates,int target,int sum,int startIndex,vector<bool>& used){if(sum == target){result.push_back(path);return;}for(int i = startIndex; i < candidates.size() && sum + candidate[i] <= target; i++){if(i > 0 && candidates[i] == candidates[i - 1]&& used[i - 1] == false){continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidate,target,sum,i + 1,used);//i+1，不能重复used[i] = false;sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>>combinationSum2(vector<int>& candidates,int target){vector<bool>used(candidates.size(),false);path.clear();result.clear();sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,0,used);return result;}
};

分割回文串

class Solution{
private:vector<vector<string>>result;vector<string>path;//回溯函数void backtracking(const string& s, int startIndex){if(startIndex >= s.size()){//到达字符串末尾，终止本次回溯result.push_back(path);//result存放最终的所有路径，即分割结果return;}for(int i = startIndex; i < s.size(); i++){if(isPalindrome(s,startIndex,i)){//是回文string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);//添加进path}else{continue;//不是，跳过}backtracking(s, i + 1);//进入i+1path.pop_back();//清空path}}//判断是不是回文串，前后双指针，正反向同步走bool isPalindrome(const string& s,int start,int end){for(int i = start, j = end; i < j; i++; j--){if(S[i] != s[j]){return false;}}return true;}public://分割函数vector<vector<string>>partition(string s){result.clear();//清除结果集path.clear();//清除路径内所有字符backtracking(s,0);//从下标0处开始对字符串分割，调用回溯函数return result;//返回结果} 
};