题目

InnoDB主键索引的B+tree在高度分别为 2 和 3 时，可以存储多少条记录？

答案

高度为2时的B+树

计算过程：

1. 使用公式 $(n\times 8+(n+1)\times 6=16\times 1024)$ 来确定一个节点可以容纳多少键/指针对。其中，$n$ 代表键的数量，每个键占用8字节，每个指针占用6字节，且每个节点的总容量为16KB。

2. 解这个方程，我们得到每个节点可以容纳的键/指针对数量 $n$ 约为1170。

3. 对于高度为2的B+树，根节点可以直接引用多达1171个叶子节点（因为指针比键多一个），每个叶子节点可以存储16条记录。

答案：

• 高度为2时，B+树可以存储的记录总数约为 $1171\times 16=18,736$ 条。

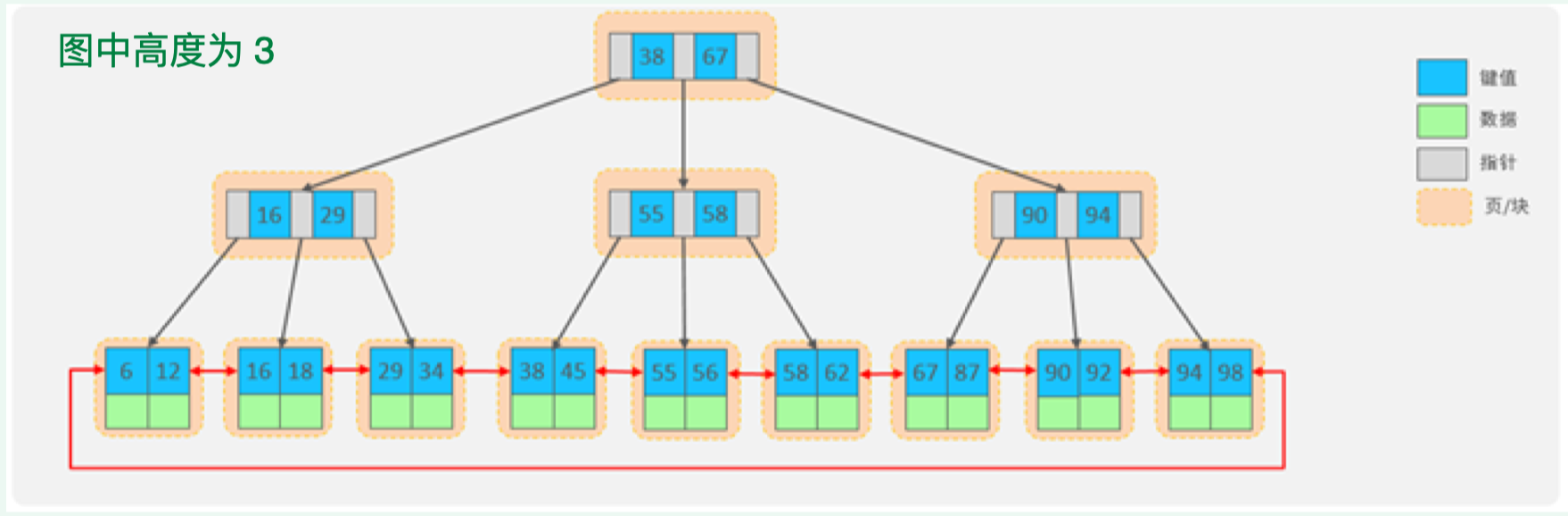
高度为3时的B+树

计算过程：

1. 在高度为3的B+树中，根节点引用中间层节点，每个中间层节点又可以引用多个叶子节点。

2. 使用同样的方式确定单个节点的容量，我们知道每个节点可以容纳约1171个键/指针对。

3. 根节点可以引用1171个中间层节点，每个中间层节点可以引用1171个叶子节点，每个叶子节点存储16条记录。

答案：

• 高度为3时，B+树可以存储的记录总数约为 $1171\times 1171\times 16=21,939,856$ 条，即约2200万条记录。

总结

• 高度为2时，B+树通过其根节点直接引用叶子节点，可以存储约18,736条记录。
• 高度为3时，B+树增加了一层中间节点，大大增加了其存储能力，可以存储约2200万条记录。

这些计算展示了B+树随着高度增加而其存储能力呈指数级增长的特性，这使得B+树成为数据库索引的理想结构，能够高效地管理大量数据。

GPT4 对话过程

https://chat.openai.com/share/fc1c15c6-43ee-4ca7-83e8-c00990806566