目录

一、程序及算法内容介绍：

基本内容：

亮点与优势：

二、实际运行效果：

三、部分代码展示：

四、完整代码+数据分享下载：

---

一、程序及算法内容介绍：

基本内容：

• 本代码基于Matlab平台编译，将PSO(粒子群算法)与LSTM（长短期记忆神经网络）结合，进行多输入数据回归预测

• 输入训练的数据包含7个特征，1个响应值，即通过7个输入值预测1个输出值（多变量回归预测）

• 归一化训练数据，提升网络泛化性

• 通过PSO算法优化LSTM网络的学习率、神经元个数参数，记录下最优的网络参数

• 训练LSTM网络进行回归预测，实现更加精准的预测

• 迭代计算过程中，自动显示优化进度条，实时查看程序运行进展情况

• 自动输出多种多样的的误差评价指标，自动输出大量实验效果图片

亮点与优势：

• 注释详细，几乎每一关键行都有注释说明，适合小白起步学习

• 直接运行Main函数即可看到所有结果，使用便捷

• 编程习惯良好，程序主体标准化，逻辑清晰，方便阅读代码

• 所有数据均采用Excel格式输入，替换数据方便，适合懒人选手

• 出图详细、丰富、美观，可直观查看运行效果

• 附带详细的说明文档（下图），其内容包括：算法原理+使用方法说明

二、实际运行效果：

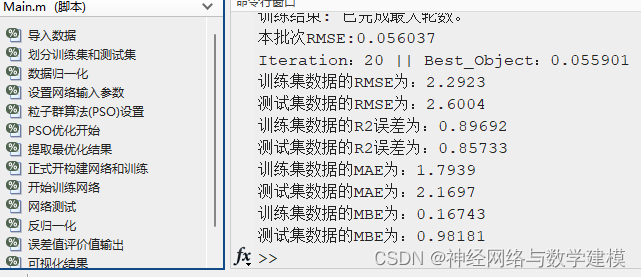
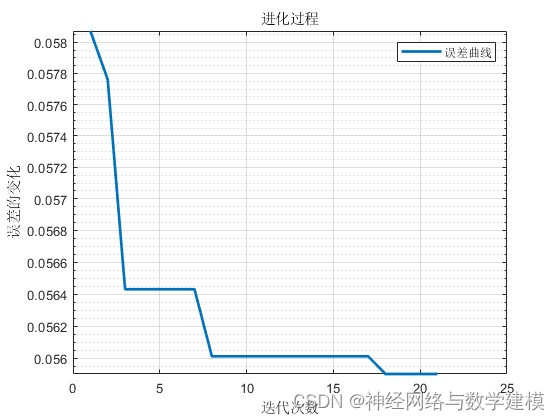
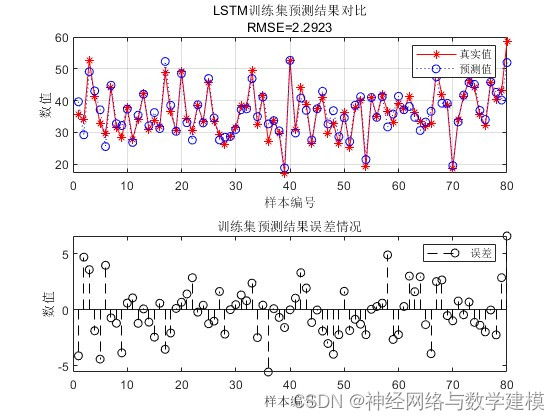
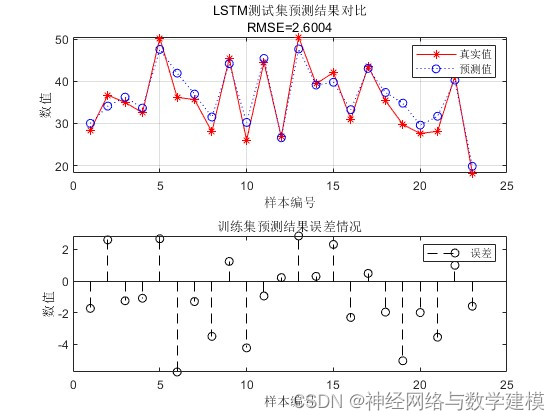
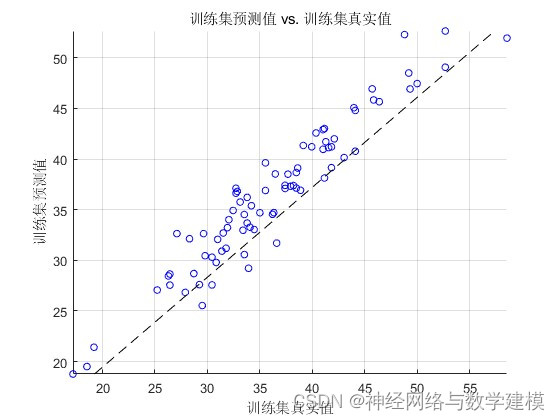
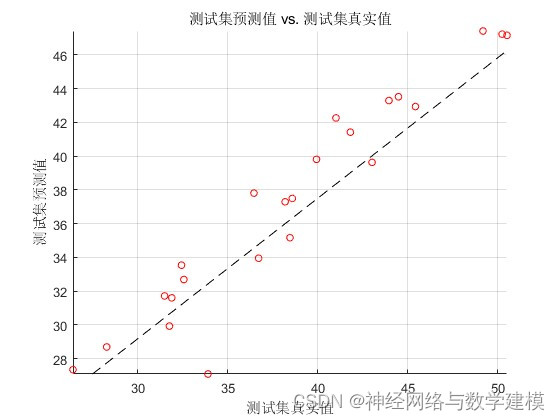
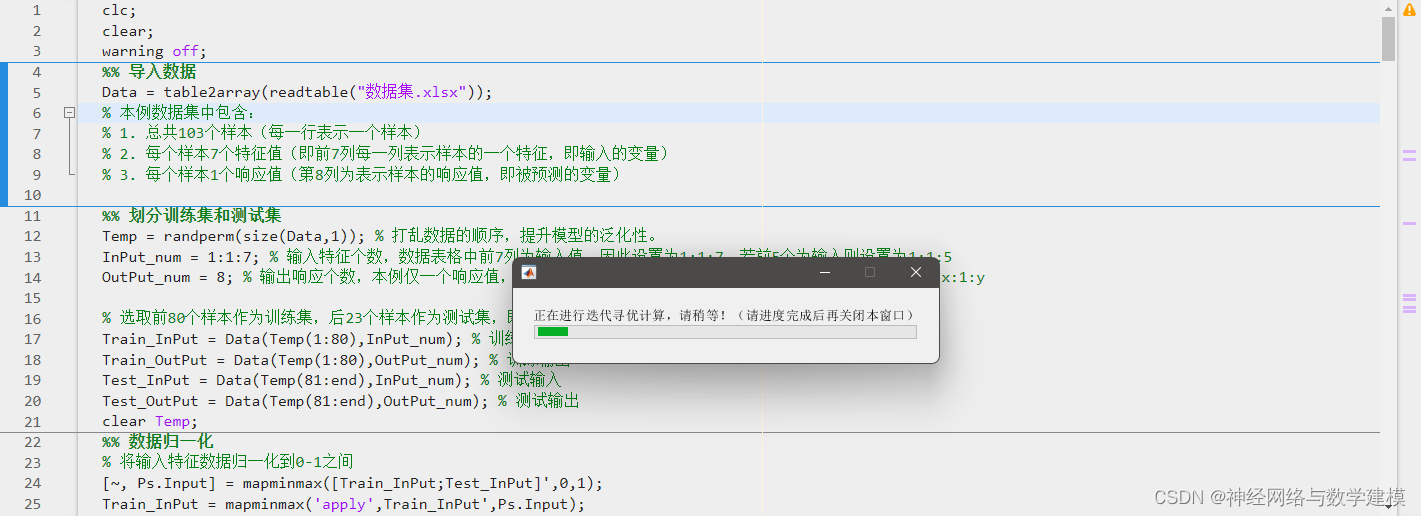
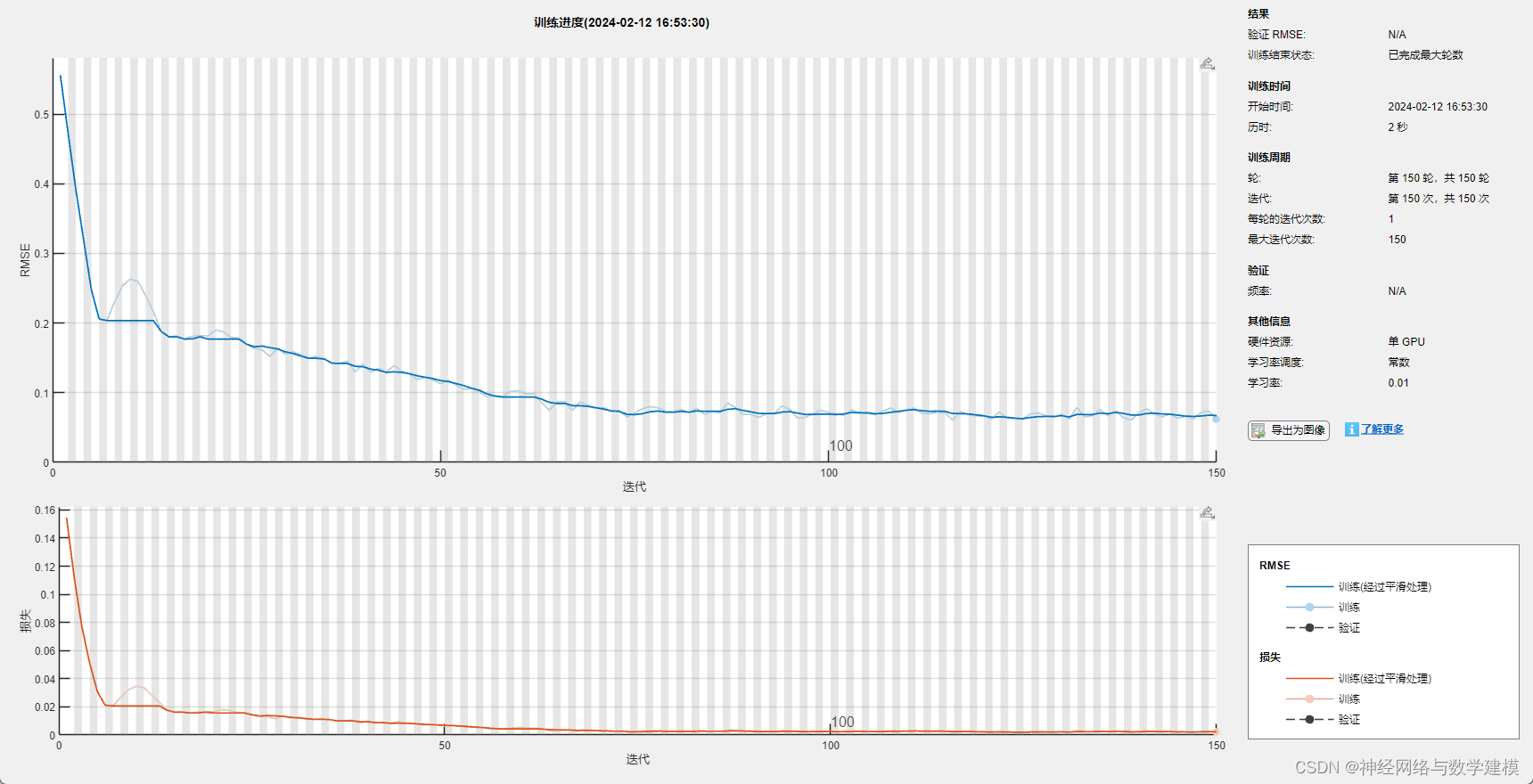
三、部分代码展示：

clc;
clear;
warning off;
%% 导入数据
Data = table2array(readtable("数据集.xlsx"));
% 本例数据集中包含：
% 1. 总共103个样本（每一行表示一个样本）
% 2. 每个样本7个特征值（即前7列每一列表示样本的一个特征，即输入的变量）
% 3. 每个样本1个响应值（第8列为表示样本的响应值，即被预测的变量）%% 划分训练集和测试集
Temp = randperm(size(Data,1)); % 打乱数据的顺序，提升模型的泛化性。
InPut_num = 1:1:7; % 输入特征个数，数据表格中前7列为输入值，因此设置为1:1:7，若前5个为输入则设置为1:1:5
OutPut_num = 8; % 输出响应个数，本例仅一个响应值，为数据表格中第8个，若多个响应值参照上行数据格式设置为x:1:y% 选取前80个样本作为训练集，后23个样本作为测试集，即（1：80），和（81：end）
Train_InPut = Data(Temp(1:80),InPut_num); % 训练输入
Train_OutPut = Data(Temp(1:80),OutPut_num); % 训练输出
Test_InPut = Data(Temp(81:end),InPut_num); % 测试输入
Test_OutPut = Data(Temp(81:end),OutPut_num); % 测试输出
clear Temp;
%% 数据归一化
% 将输入特征数据归一化到0-1之间
[~, Ps.Input] = mapminmax([Train_InPut;Test_InPut]',0,1); 
Train_InPut = mapminmax('apply',Train_InPut',Ps.Input);
Test_InPut = mapminmax('apply',Test_InPut',Ps.Input);
% 将输出响应数据归一化到0-1之间
[~, Ps.Output] = mapminmax([Train_OutPut;Test_OutPut]',0,1);
Train_OutPut = mapminmax('apply',Train_OutPut',Ps.Output);
Test_OutPut = mapminmax('apply',Test_OutPut',Ps.Output);
Temp_TrI = cell(size(Train_InPut,2),1);
Temp_TrO = cell(size(Train_OutPut,2),1);
Temp_TeI = cell(size(Test_InPut,2),1);
Temp_TeO = cell(size(Test_OutPut,2),1);

四、完整代码+数据分享下载：