题目链接:LCR 047. 二叉树剪枝 - 力扣(LeetCode)
题目:
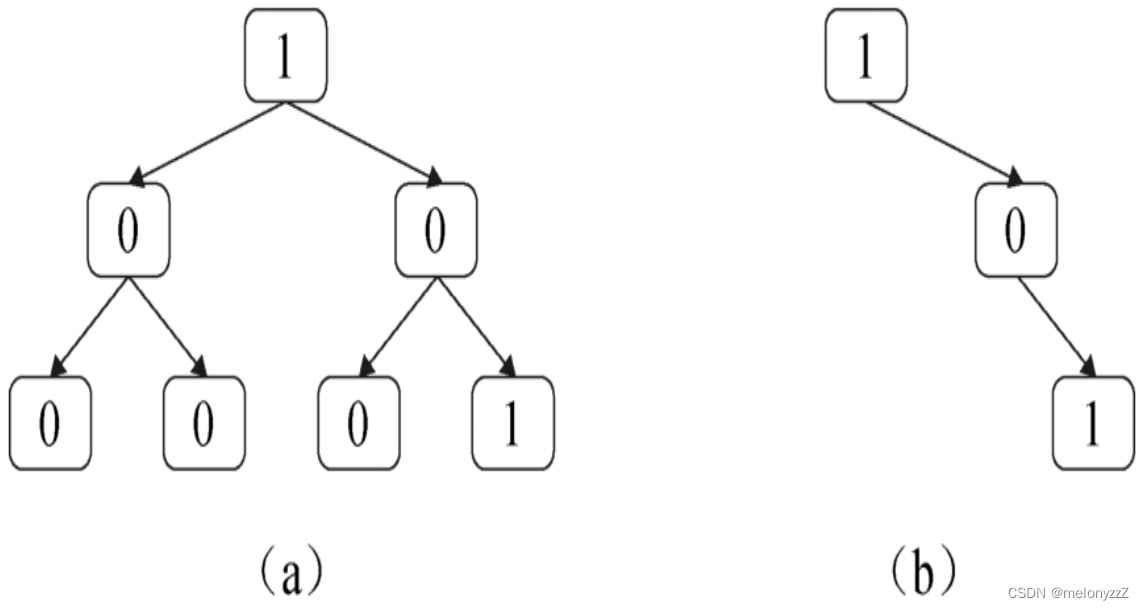
一棵二叉树的所有节点的值要么是 0 要么是 1,请剪除该二叉树中所有节点的值全都是 0 的子树。例如,在剪除下图 (a) 中二叉树中所有节点值都为 0 的子树之后的结果如下图 (b) 所示。
分析:
首先分析哪些子树会被剪除,哪些子树不能被剪除。在上图 (a) 的二叉树中,以第 2 层第 1 个节点为根节点的子树的 3 个节点的值都是 0,因此整棵二叉树都被剪除。以第 2 层第 2 个节点为根节点的子树中有一个节点的值是 1(第 3 层第 4 个节点),因此这棵子树不能删除,但是它的左子树(根节点为第 3 层第 3 个节点)只有一个节点并且值为 0,因此它的左子树可以被剪除。
下面总结什么样的节点可以被删除。首先,这个节点的值应该是 0。其次,如果它有子树,那么它的子树的所有节点的值都为 0。也就是说,如果一个节点可以被删除,那么它的子树的所有节点都可以被删除。例如,在上图 (a) 的二叉树中,第 2 层第 1 个节点可以被删除,它的子树中的所有节点(第 3 层第 1 个节点和第 2 个节点)也可以被删除。
由此发现,后序遍历最适合用来解决这个问题。如果用后序遍历的顺序遍历到某个节点,那么它的左右子树的节点一定已经遍历过了。每遍历到一个节点,就要确定它是否有左右子树,如果左右子树都是空的,并且节点的值是 0,那么就可以删除这个节点。
代码实现:
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if (!root)return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);if (!root->left && !root->right && root->val == 0)return nullptr;return root;}
};

![[office] Excel设置打印表头 #学习方法#学习方法#微信](https://img-blog.csdnimg.cn/img_convert/bc3da58a57ba5b74944dbb3d1d6ba3d2.png)