A

输出最大值减最小值，或者排序算一下答案

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define inf 0x3f3f3f3f*1llusing namespace std;void solve()
{int n;cin>>n;vector<int>a(n+1);rep(i,1,n){cin>>a[i];}sort(a.begin()+1,a.end());int res=0;rep(i,2,n){res+=a[i]-a[i-1];}cout<<res<<endl;
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;cin>>_;while(_--)solve();return 0;
}

B

B还wa了一发，有点难受一开始推错了，写的太慢了
思路：
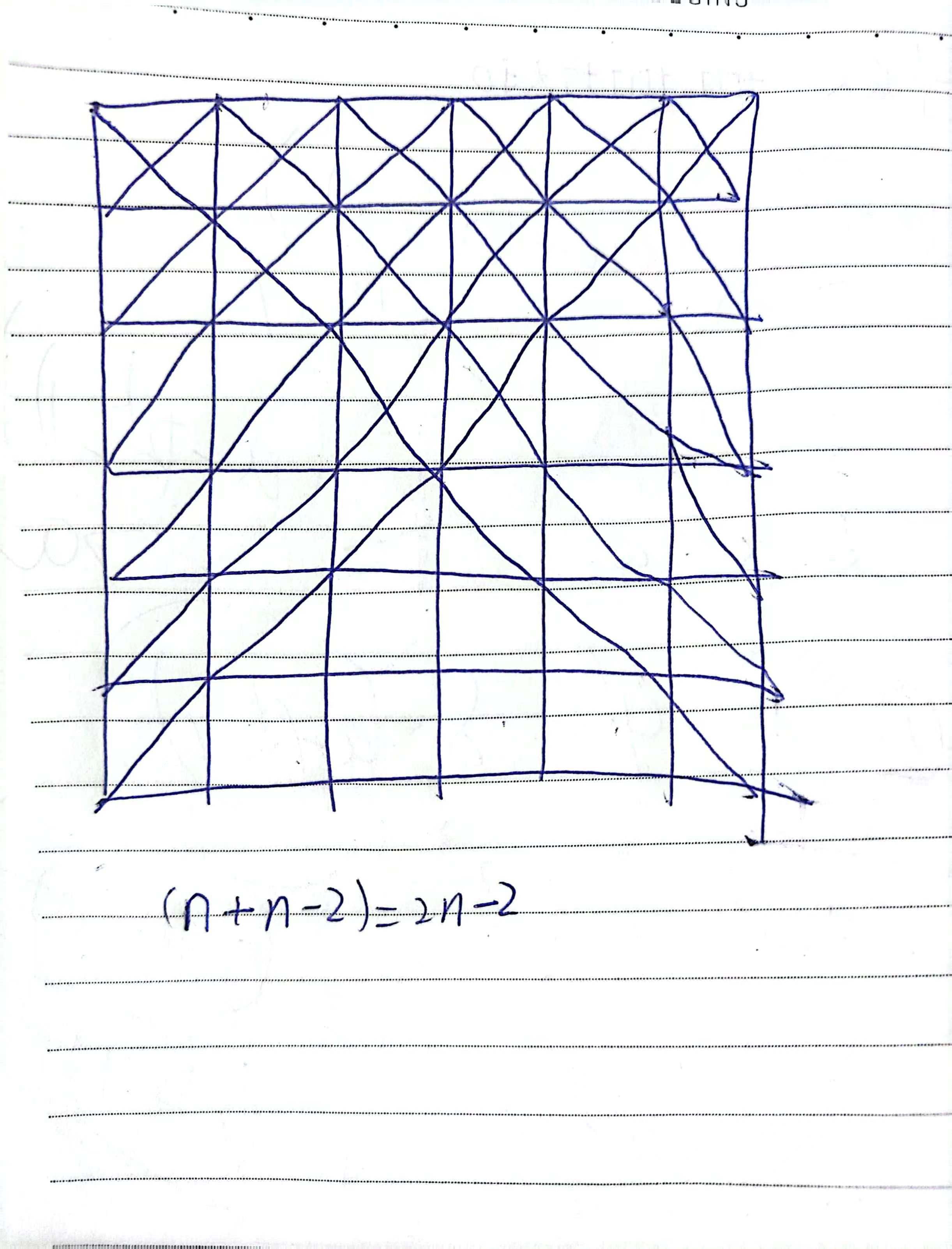
考虑对答案能贡献2的放格有多少个。
上面一行$n$个能对答案贡献$2$，下面一行除了两端的两个都能对答案贡献2
所以一共能贡献2的方格有$2\ast n-2$个

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define inf 0x3f3f3f3f*1llusing namespace std;void solve()
{int n,k;cin>>n>>k;int num2=2*n-2;if(k>2*num2){cout<<num2+k-num2*2<<endl;}else{cout<<k/2+(k%2!=0)<<endl;}
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;cin>>_;while(_--)solve();return 0;
}

C

c题溢出了中间应该提前结束
推公式
考虑每次的下注如果在这一轮赢得话就要把之前所有输的钱全部赢回来有点类似倍投的思想】
从一1开始，之前的下注总和记为$sum$
下一轮下注要下$sum/(k-1)+1$才能赢钱
中间如果$sum>a$的话要提前结束，说明下不到就会没钱了

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define inf 0x3f3f3f3f*1llusing namespace std;void solve()
{int k,x,a;cin>>k>>x>>a;int sum=0;rep(i,1,x){if(sum>a){cout<<"NO"<<endl;return;}sum+=sum/(k-1)+1;}if((a-sum)*(k-1)>sum){cout<<"YES"<<endl;}else{cout<<"NO"<<endl;}
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;cin>>_;while(_--)solve();return 0;
}

D

树形dp思路参考的是b站的一个题解
这题和c题的题目描述感觉都有点抽象很难懂。
题意：让我们求点集的方案数，点集中没有3个点在一条直线。
$f[u][0]:表示以u为根节点的子树中，危险结点数为0个的方案总数$
$f[u][1]:表示以u为根节点的子树中，危险结点数为1个的方案总数$
$f[u][2]:表示以u为根节点的子树中，危险结点数为2个的方案总数$
考虑状态转移
$f[u][0]=1$只能当前u这个结点是危险结点时，满足
$f[u][1]\ast =(f[v][0]+f[v][1])$当前结点可能是危险结点，也可能不是，
如果是危险结点那么上一个结点就不是危险结点，如果当前结点不是危险结点，那么上一个一定是危险结点
$f[u][2]=(f[u][2]+f[u][1])$:讨论同$f[u][1]$

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;
const int mod=998244353;
void solve() {int n;cin>>n;vector<vector<int>>g(n+1);rep(i,1,n-1){int u,v;cin>>u>>v;g[u].pb(v);g[v].pb(u);}vector<vector<int>>f(n+1,vector<int>(3));auto dfs=[&](auto &&dfs,int u,int fa)->void{f[u][0]=1;f[u][1]=1;for(auto v:g[u]){if(v==fa){continue;}dfs(dfs,v,u);f[u][1]*=(f[v][0]+f[v][1]);f[u][2]+=f[v][2]+f[v][1];rep(i,0,2){f[u][i]=(f[u][i]+mod)%mod;}}};dfs(dfs,1,-1);int ans=0;rep(i,0,2){ans=(ans+f[1][i])%mod;}cout<<(ans+mod)%mod<<endl;
}signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//	freopen("1.in", "r", stdin);int _;cin>>_;while(_--)solve();return 0;
}