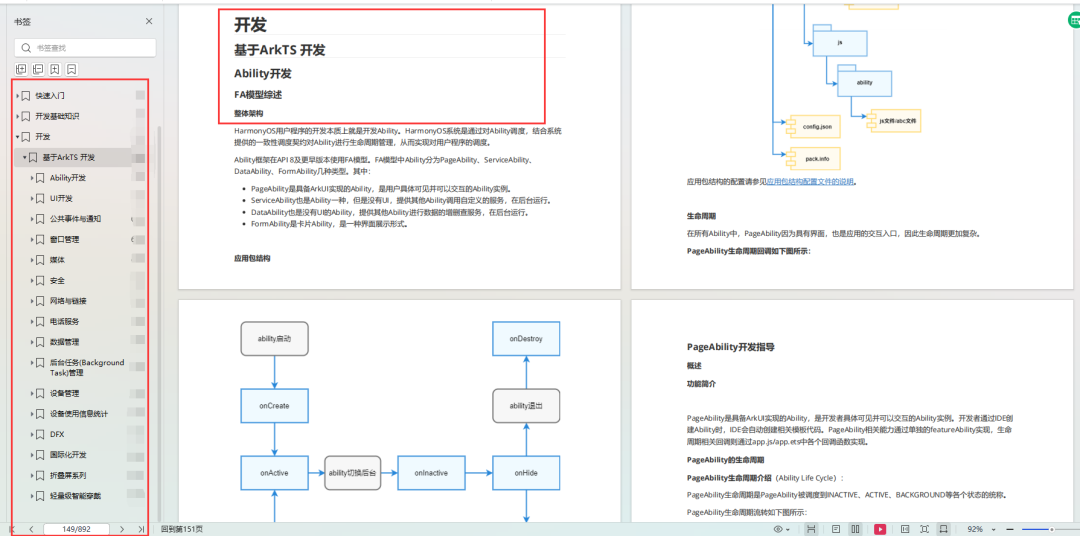
差分对的主要目的是为了保持正确的差分阻抗，因此，必须了解差分阻抗的含义，差分阻抗是每条走线奇模阻抗的两倍，而每条走线的单端阻抗（SE, single-ended），仅当差分线内没有对内耦合时，才等于奇模阻抗，因此，当两根走线更加靠近彼此时，差分阻抗会降低，此时就需要通过调整线宽对其进行补偿。 如下图所示，展示了一对边缘耦合的带状走线，上图展示了一对松散耦合状态下（线间距=3.5*线宽）的走线电磁场分布，下图展示了一对紧密耦合状态下（线间距=1.5*线宽）的走线电磁场分布，红色代表流入页面的电流方向，蓝色代表流出页面的电流方向，并且，环绕走线的圆曲线代表磁场，而电场则垂直于磁场。 可以观察到，当走线松散耦合时，每条走线周围的电场线和磁场线几乎是对称的，并且，大多数电场与上下的参考面耦合，而当走线彼此靠近形成紧密耦合时，线间的磁场线被压缩，电场线则更多地倾向于相互耦合，由于电磁场的相互作用的增强，就好像线之间形成了一个参考面。

奇模（Odd-Mode）阻抗

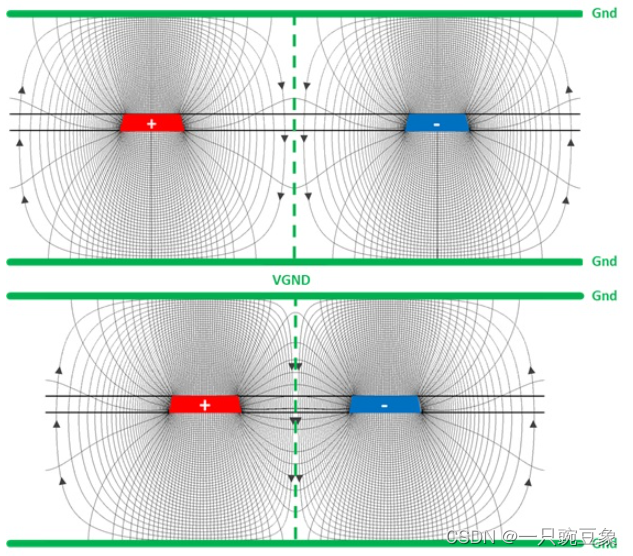
        如下图所示，一对等宽的微带线模型，当考虑单独驱动1号线时，产生了单端特性阻抗Z0，它由相对于参考地平面的自环路电感L11和自电容C11组成，当考虑差分驱动1和2号线时，传播模态变为了奇模，将会产生如前一张图所示的电磁场相互耦合作用，并且由互感Lm和互容Cm进行耦合描述。 

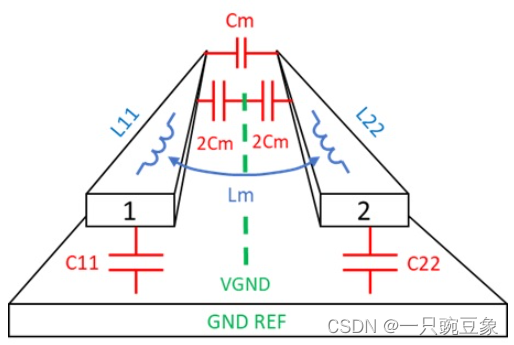
        在二维场求解器中，就可以利用上述参数，建立如下的LC矩阵：

        LC矩阵可以用来确定奇模阻抗，它可以用下面的等式来计算：

        举例说明各个参数之间的关系：

        使用Polar SI9000二维场求解器比较了具有W1=4 mil走线、间隔S1=20 mil空间的松散耦合差分（Loose）对与具有相同介电厚度的SE传输线，LC矩阵在10GHz频带提取，从结果上可以看出，松耦合对的奇模阻抗等于SE走线的特性阻抗，因此差分阻抗是相同的，因为此时的互感和互容值都特别地小，几乎可以等同于零。

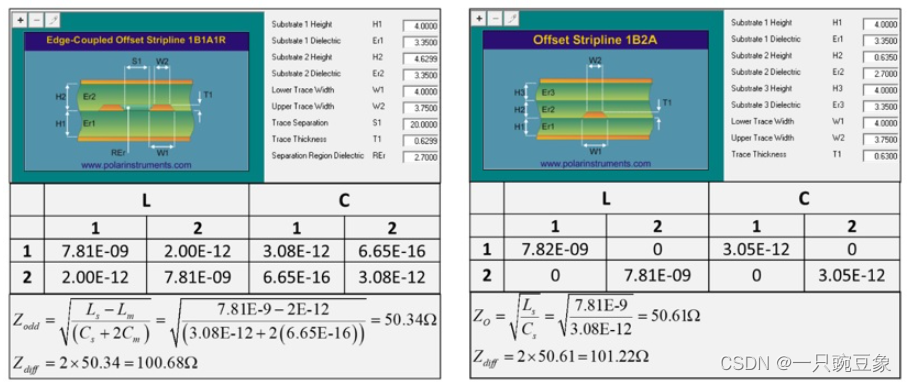
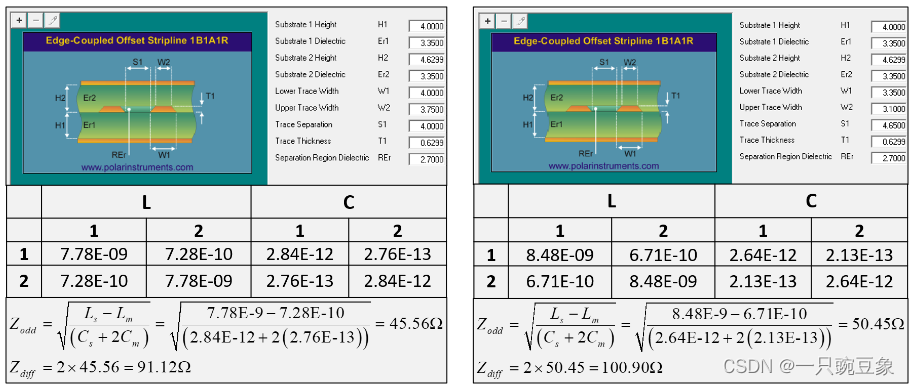
        但是，如果布线一对紧密耦合的走线，则相同走线宽度下的奇模阻抗小于SE阻抗，如下图的左侧（Tight1），H1-W1-S1为4-4-4mil几何结构的差分阻抗为91欧姆，因为此时的互感和互容值都增大了，根据公式，会导致Zodd的减小；为了保持100欧姆差分阻抗，如下图的右侧（Tight2），线宽W1必须减少到3.35mil，线间距S1增大到4.65mil，以此弱化互感和互容的影响。

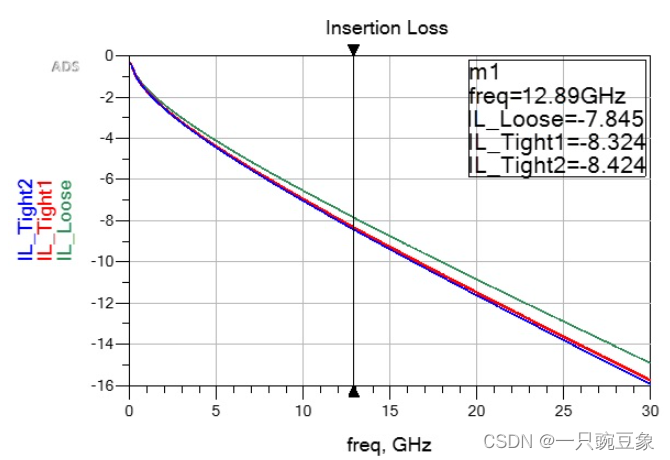
        在实际设计中，不仅要保持差分阻抗的稳定，插入损耗指标同样非常重要，因为线宽减小和耦合更紧密同样会导致长距离通道上的损耗更高，使用上述的三种差分阻抗参数（Losse/Tight1/Tight2），绘制了三个差分对的插入损耗曲线，其中，松耦合以绿色显示，不调整线宽的紧密耦合 （Tight1） 显示为红色，而线宽调节后的紧密耦合 （Tight2） 显示为蓝色，如图中标记所示，在12.89 GHz处，松耦合具有明显更低的插损效果，而Tight1 和 Tight2 之间只有 0.1 dB 的差别，这就说明无论是否调整线宽以满足差分阻抗，紧密耦合都会降低插损效果。

        综上所述，差分对是紧密耦合还是松散耦合并不重要，如果设计得当，两者都可以设计为正确匹配驱动器阻抗，其差别在于，更紧密的耦合可以提供更好的布线密度，但代价是更高的插入损耗，而松耦合可以更轻松地减少插入损耗，无论最终决定采用哪种设计，都必须针对差分阻抗进行仿真和测量，并且，由于互耦参数的存在，不能通过测量SE阻抗来确定差分阻抗。

参考文档：

        What is Differential Impedance and Why do We Care?  Bert Simonovich