leetcode刷题记录：暴力搜索算法01

参考：labuladong的算法小抄 https://labuladong.online/algo/essential-technique/backtrack-framework/
这篇太牛了，一个模板把所有的排列组合子集问题全秒了。

1. 简介

暴力搜索算法：回溯、dfs、bfs。这些都可以看做是从二叉树算法衍生出来的。

解决一个回溯问题，实际上是在遍历一颗决策树的过程。树的每个叶子结点上存着一个答案。把整棵树遍历一遍，把叶子结点上的答案都收集起来，就能得到所有的合法答案。
回溯算法的框架

result = []
def backtrack(路径，选择列表):if 满足条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择

核心是for循环里的递归，在递归前做选择，递归后撤销选择。

2. 全排列问题

leetcode 46
https://leetcode.cn/problems/permutations/
时间复杂度: O(n!)

class Solution(object):def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""if not nums:returnused = [False] * len(nums)self.res = []self.backtrack(nums, [], used)return self.resdef backtrack(self, nums, track, used):if len(track) == len(nums):self.res.append(track[:])returnfor i, n in enumerate(nums):if used[i]:continuetrack.append(n)used[i] = Trueself.backtrack(nums, track, used)track.pop()used[i] = False

3. N皇后问题

https://leetcode.cn/problems/n-queens/

回溯思想：棋盘的每一行代表决策树的每一层。每个节点可以做出的选择是，在该行的任意一个位置放置一个皇后。
isValid只需要检查上方、左上方和右上方的情况。下面的棋盘都是空的

class Solution(object):def solveNQueens(self, n):""":type n: int:rtype: List[List[str]]"""if n == 0:return 0board = [["." for _ in range(n)] for _ in range(n)]self.res = []self.backtrack(board, 0)return self.resdef backtrack(self, board, row):if row == len(board):self.res.append([''.join(x[:]) for x in board])returnn = len(board)for col in range(n):if self.isValid(board, row, col):board[row][col] = 'Q'self.backtrack(board, row+1)board[row][col] = '.'def isValid(self, board, row, col):n = len(board)# 检查列for i in range(row):if board[i][col] == 'Q':return False# 检查左上方r,c = row-1, col-1while r >=0 and c >= 0:if board[r][c] == 'Q':return Falser -= 1c -= 1# 检查右上方r,c = row-1, col+1while r >=0 and c <= n-1:if board[r][c] == 'Q':return Falser -= 1c += 1return True

4. 所有排列、组合、子集问题

4.1 问题抽象

排列、组合、子集问题，都是给定序列nums，从中选出若干个元素的问题。

形式一：nums的元素无重复，不可重复选。
形式二：nums的元素有重复，不可重复选。
形式三：nums的元素无重复，可以重复选。
作图：
子集、组合数：
排列数：

4.2 leetcode 78 子集

https://leetcode.cn/problems/subsets/
nums元素无重复，不可重复选
决策树图：
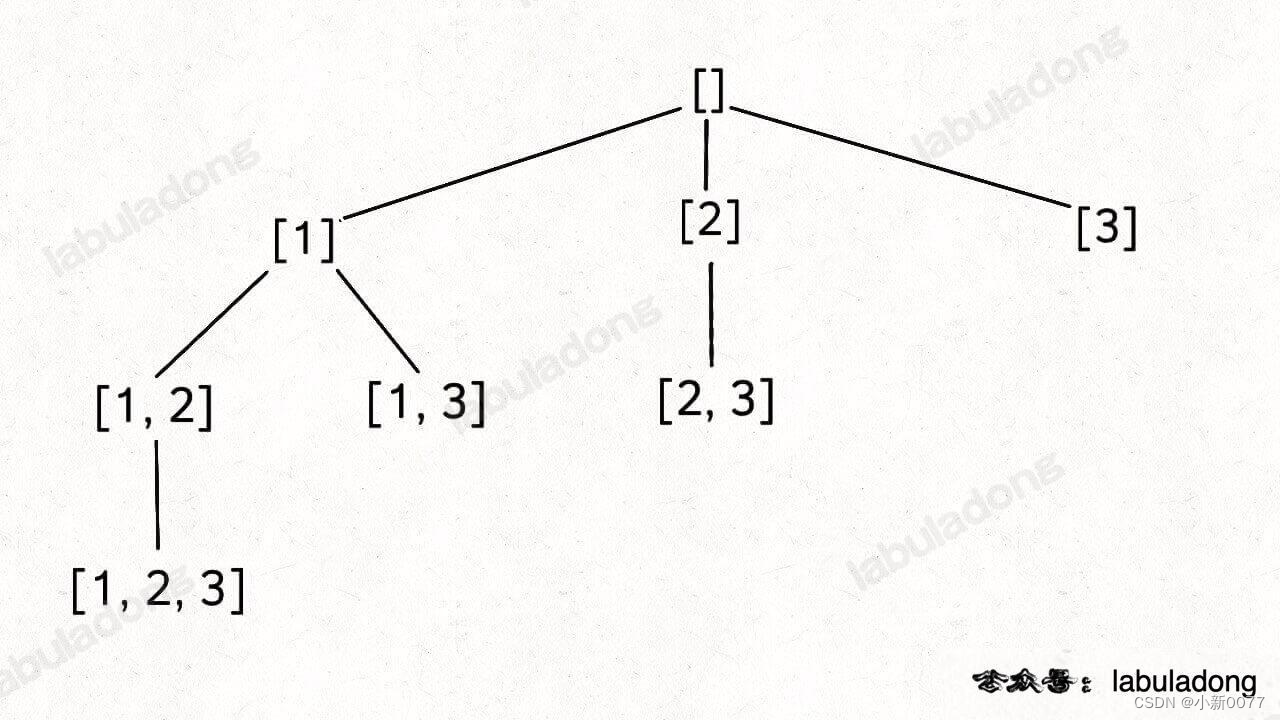
在这里插入图片描述

用start + for循环控制子集元素不重复。
其实这里就相当于整个决策树的遍历。self.res.append(self.track[:])在前序位置将结果插入到res中；for循环就是遍历所有的子树。这里通过start来控制不会收集重复的元素。

class Solution(object):def subsets(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""self.res = []self.track = []self.backtrack(nums, 0)return self.resdef backtrack(self, nums, start):self.res.append(self.track[:])for i in range(start, len(nums)):self.track.append(nums[i])self.backtrack(nums, i+1)self.track.pop()

4.3 leetcode 77 组合

https://leetcode.cn/problems/combinations/description/
和子集非常类似，nums元素无重复，不可重复选

class Solution(object):def combine(self, n, k):""":type n: int:type k: int:rtype: List[List[int]]"""self.res = []self.track = []self.backtrack(n, k, 1)return self.resdef backtrack(self, n, k, start):if len(self.track) == k:self.res.append(self.track[:])returnfor i in range(start, n+1):self.track.append(i)self.backtrack(n, k, i+1)self.track.pop()return

4.4 leetcode 90 子集II

https://leetcode.cn/problems/subsets-ii/description/
元素可重复，不可重复选取
这道题的思路很重要。以[1,2,2]为例，我们把第二个2叫做2’，画出决策树的图：
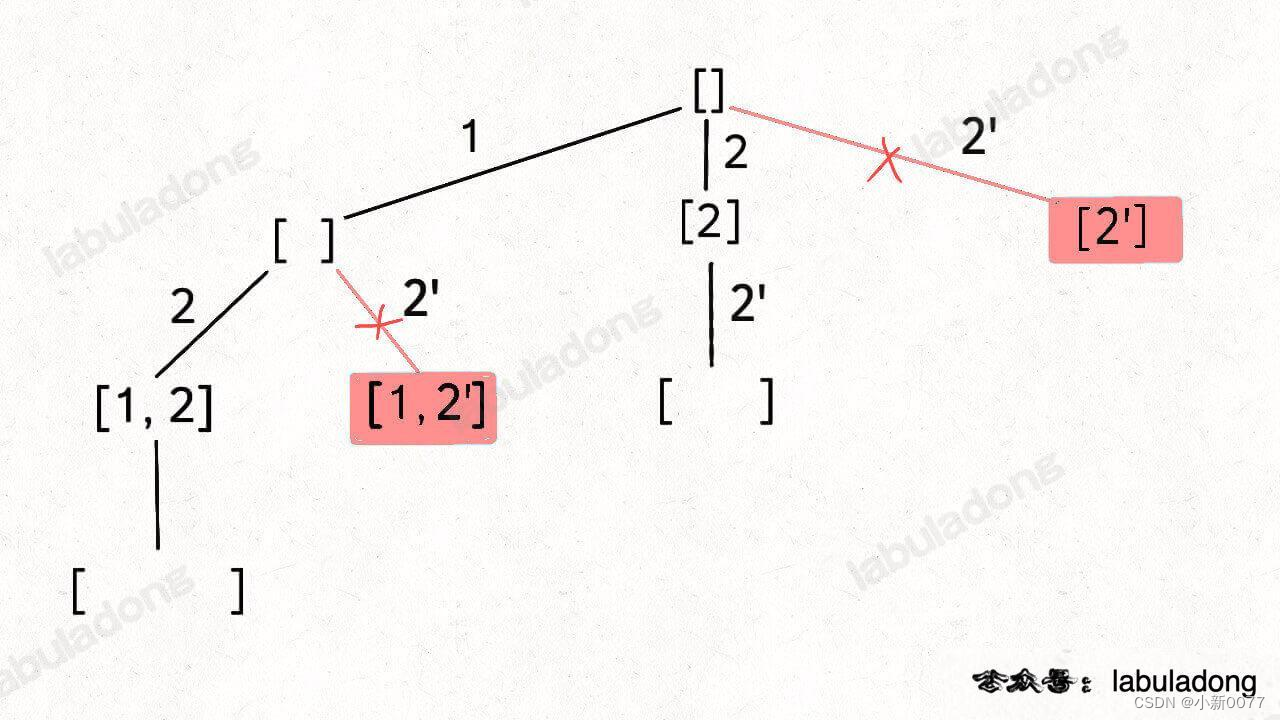
在这里插入图片描述

可以看到用决策树中出现了重复，要进行剪枝。这里和子集I的区别在于，如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历。
如何在代码中实现剪枝呢？首先要对nums排序，让相同元素都靠在一起。
其次，在for循环遍历中，如果i > start且nums[i] == nums[i-1]，则跳过。i > start很重要。i= start代表这是结点的第一个分支，无论如何不应该跳过。否则[2,2]和[1,2,2]就会被漏掉

class Solution(object):def subsetsWithDup(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""nums.sort()self.res = []self.track = []self.backtrack(nums, 0)return self.resdef backtrack(self, nums, start):self.res.append(self.track[:])for i in range(start, len(nums)):if i > start and nums[i] == nums[i-1]: # i > start很重要。i= start代表这是结点的第一个分支，无论如何不应该跳过。否则[2,2]和[1,2,2]就会被漏掉continueself.track.append(nums[i])self.backtrack(nums, i+1)self.track.pop()return

4.5 leetcode40 组合总和

https://leetcode.cn/problems/combination-sum-ii/description/
上面子集II的变体，把res.append的条件稍微改一下即可。

class Solution(object):def combinationSum2(self, candidates, target):""":type candidates: List[int]:type target: int:rtype: List[List[int]]"""self.res = []self.track = []candidates.sort()self.backtrack(candidates, target, 0)return self.resdef backtrack(self, candidates, target, start):if sum(self.track) == target:self.res.append(self.track[:])returnfor i in range(start, len(candidates)):if sum(self.track) + candidates[i] > target:continueif i > start and candidates[i] == candidates[i-1]:continueself.track.append(candidates[i])self.backtrack(candidates, target, i+1)self.track.pop()return

4.6 leetcode47 全排列II

https://leetcode.cn/problems/permutations-ii/description/
数组元素可重复
这里和全排列的框架一样，只是对数组排了序，并添加了一个剪枝的策略.重点在于我们如何剪枝？
标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复。
体现在代码上，就是我们先对nums排序，然后把2, 2’看做是有序的. 如果2没有在track中出现，那么2’就不应该添加到track中.

class Solution(object):def permuteUnique(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""self.res = []self.track = []self.used = [False] * len(nums)nums.sort()self.backtrack(nums)return self.resdef backtrack(self, nums):if len(self.track) == len(nums):self.res.append(self.track[:])returnfor i, n in enumerate(nums):if self.used[i]:continue# 重点if i > 0 and nums[i] == nums[i-1] and not self.used[i-1]:continueself.used[i] = Trueself.track.append(n)self.backtrack(nums)self.track.pop()self.used[i] = False

4.7 leetcode39 组合总和

https://leetcode.cn/problems/combination-sum/
可重复选取数字
看起来麻烦，但实际上非常简单。
先想一下，不可重复选取数字的时候，我们是通过start = i + 1来控制不重复的。这里让start=i就可以重复选取了。easy!

class Solution(object):def combinationSum(self, candidates, target):""":type candidates: List[int]:type target: int:rtype: List[List[int]]"""self.res = []self.track = []self.backtrack(candidates, target, 0)return self.resdef backtrack(self, nums, target, start):if sum(self.track) == target:self.res.append(self.track[:])returnfor i in range(start, len(nums)):if sum(self.track) + nums[i] > target:continueself.track.append(nums[i])self.backtrack(nums, target, i)self.track.pop()

4.8 leetcode没有，自己总结：可重复选取元素的全排列

和全排列类似，把used函数的控制去掉即可。

5. 总结：一个模板秒杀所有排列、组合、子集问题。

5.1 nums无重复，不可重复选取

#组合、子集问题
res, track  = [], []
def backtrack(nums, start):# 1. 退出条件if xxx:res.append(track[:])return# 2. 回溯框架for i in range(start, len(nums)):track.append(nums[i])backtrack(nums, i+1)track.pop()
#排列问题
res, track, used  = [], [], [False]*len(nums)
def backtrack(nums):# 1. 退出条件if xxx:res.append(track[:])return# 2. 回溯框架for i in range(len(nums)):if used[i]:continueused[i] = Truetrack.append(nums[i])backtrack(nums)used[i] = Falsetrack.pop()

5.2 nums有重复，不可重复选取

对nums排序
剪枝：
– 组合、子集：当i > start and nums[i] == nums[i-1]时剪枝
– 排列：当i > 0 and nums[i] == nums[i-1] and !used[i-1]时剪枝

#组合、子集问题
res, track  = [], []
def backtrack(nums, start):# 1. 退出条件if xxx:res.append(track[:])return# 2. 回溯框架for i in range(start, len(nums)):if i > start and nums[i] == nums[i-1]track.append(nums[i])backtrack(nums, i+1)track.pop()
#排列问题
res, track, used  = [], [], [False]*len(nums)
def backtrack(nums):# 1. 退出条件if xxx:res.append(track[:])return# 2. 回溯框架for i in range(len(nums)):if used[i]:continue# 剪枝if i > 0 and nums[i] == nums[i-1] and not used[i-1]:continueused[i] = Truetrack.append(nums[i])backtrack(nums)used[i] = Falsetrack.pop()

5.3 nums无重复，可重复选取

组合、子集：递归时start = i
排列：放飞自我，把used判断去掉

#组合、子集问题
res, track  = [], []
def backtrack(nums, start):# 1. 退出条件if xxx:res.append(track[:])return# 2. 回溯框架for i in range(start, len(nums)):if i > start and nums[i] == nums[i-1]track.append(nums[i])backtrack(nums, i)track.pop()
#排列问题
res, track  = [], []
def backtrack(nums):# 1. 退出条件if xxx:res.append(track[:])return# 2. 回溯框架for i in range(len(nums)):track.append(nums[i])backtrack(nums)track.pop()