"The greatest glory in living lies not in never falling, but in rising every time we fall." - Nelson Mandela

1. 题目描述

2. 题目分析与解析
2.1 思路一——暴力求解
还是和之前讲的一样,看见题目没思路,先试试普通情况下人的解法,也就是暴力求解。如果让一个人来解决该题目,那就是尝试从S字符串的每个位置作为起始位置,然后向后遍历,看是否能那囊括所有 t 中的字符,能囊括就记录位置与长度,不能囊括就记录为空,最后返回最短的子串。
代码思路:
-
初始化,对于 t 中字符,使用一个hashMap存储,键为字母,值为出现的次数
-
外层for循环遍历 s 中所有字符,作为起始字符
-
内层for循环遍历以每个起始字符出发向后尝试囊括 t 中字符
-
走到 s 尾部仍然不行,那就返回空串 (因为第一个字符作为起始位置都不能涵盖 t 所有字符,那也就是遍历了整个 s 都无法涵盖t,肯定无解)
-
能够囊括便停止,记录起始位置和终止位置
-
-
返回最短的解
但是很显然,这种算法时间复杂度很高,通过嵌套循环遍历字符串s,试图找到包含t中所有字符的最小窗口。对于s中的每一个字符(外层循环),它会迭代剩余的字符(内层循环)来找到这样的窗口。这导致了最坏情况下的时间复杂度为O(n^2),其中n是字符串s的长度。这是因为对于s中的每个字符,我们在最坏的情况下可能需要扫描它右侧的每个其他字符。同时还需要遍历 t 字符串,因此导致时间复杂度为O(n^2 \cdot m)。
现在我们考虑如何优化代码。
2.2 思路二——滑动窗口
这个题目起始和上一篇文章《串联所有单词的子串》题目非常的相似,如果大家对于滑动窗口没有解决该题目没有什么头绪可以先回头看看上个题目。
因为和上一篇内容十分相似,我就直接给出解决办法。
-
我们需要指定一个左右指针,开始时左右指针都指向 s 的首字符,然后右指针不断向右移动,直到囊括了 t (也就是找到了第一个解)。
-
这时我们移动左指针,将左指针不断加一,并判断在这种情况下是否还能囊括 t ,如果出现了不能囊括的情况,我们继续移动右指针,直到再次囊括 t 。
-
然后继续移动左指针不断加一,并判断在这种情况下是否还能囊括 t ,以此循环,直到右指针走到结尾。
这样做之所以是正确的是因为每一次左指针的移动实际上就是以左指针指向的字符作为开始位置的判断(类似于暴力求解将,以左指针作为起始字符,向后寻找解)。
而之所以这样做很高效就是因为我在每一个位置都能利用窗口中的信息,从而减少了对窗口部分的判断,大大缩减了时间开销。
代码思路:
-
初始化哈希表
-
窗口计数表(windowCounts):同时,创建另一个哈希表来追踪当前滑动窗口中每个字符出现的次数。
-
频率表(freqMap):首先创建一个哈希表来存储字符串
t中每个字符出现的次数。这是因为我们需要知道窗口中必须包含哪些字符,以及这些字符各需要出现多少次,才能认为窗口满足条件。
-
-
使用两个指针表示窗口的边界
-
左指针(left)和右指针(right):这两个指针分别表示当前考察的窗口的左右边界。初始时,两者都指向字符串
s的开始位置。
-
-
扩大窗口
-
如果窗口中某个字符的数量达到了
t中该字符所需的数量,则认为该字符已被“完全覆盖”。 -
移动右指针
right来扩大窗口,每次右移一位,并更新windowCounts中对应字符的计数。
-
-
收缩窗口
-
在收缩的过程中,如果移除的字符是
t中的必需字符,且其数量减少到小于t中所需的数量,则更新formed,表示窗口不再满足条件。 -
当窗口已包含所有
t中的字符(即formed(用来跟踪当前窗口中完全匹配t中所有字符所需的唯一字符数)等于freqMap的大小时),尝试通过移动左指针left来收缩窗口,以找到可能的最小窗口。
-
-
更新最小窗口
-
在每次窗口变动(扩大或收缩)后,如果当前窗口满足所有
t中字符的要求(即formed等于freqMap的大小),就比较并更新保存最小窗口的变量(如窗口大小、起始位置等)。
-
-
结果输出
-
最终,根据保存的最小窗口信息输出最小窗口子串。如果没有找到满足条件的窗口,则返回空字符串。
-
这种方法的优势在于它通过动态地调整窗口的大小来寻找最小满足条件的窗口,同时利用哈希表来有效地追踪和更新窗口内字符的情况,从而避免了不必要的字符串操作,提高了算法的效率。
3. 代码实现
3.1 暴力求解


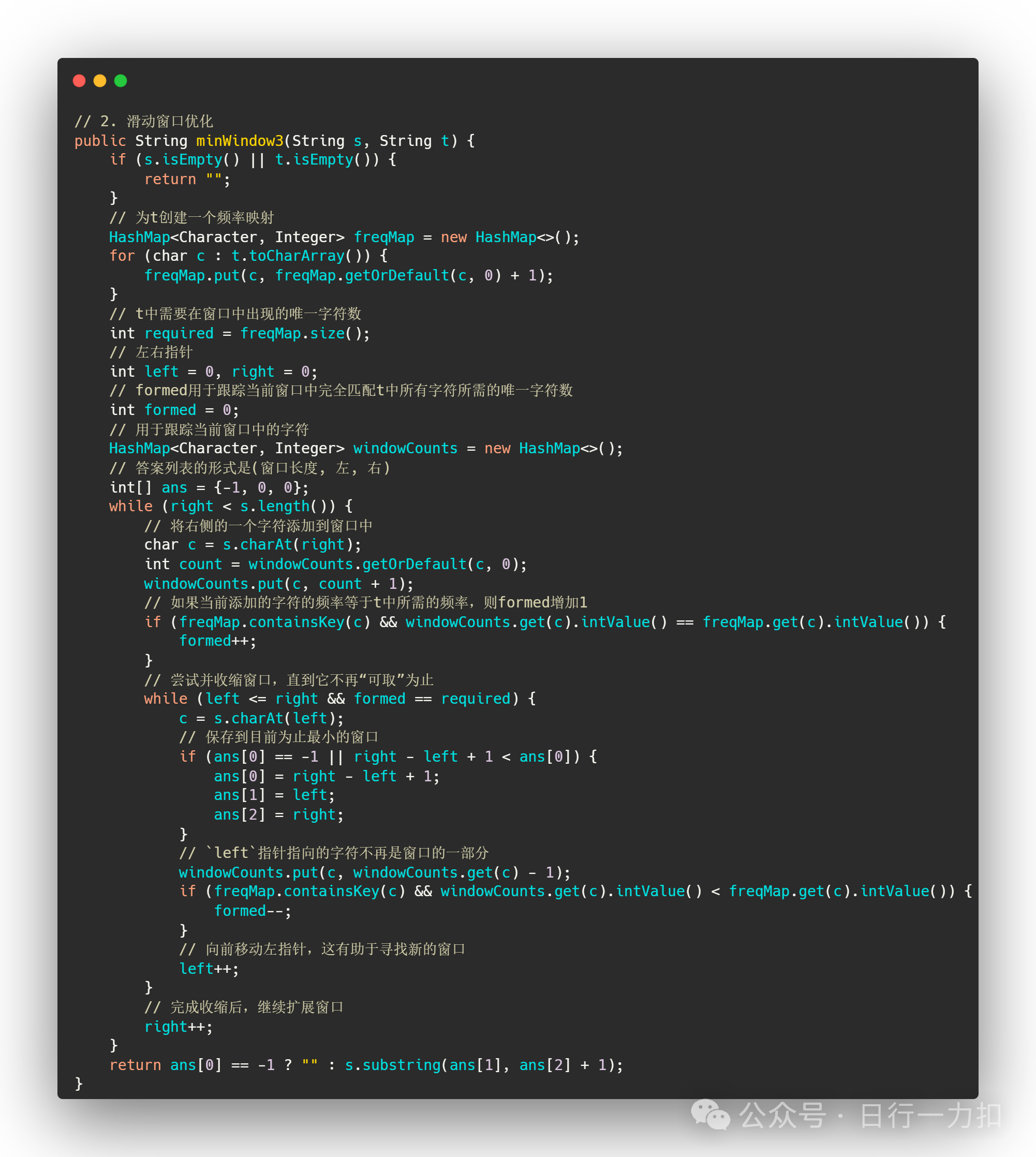
3.2 滑动窗口
4. 相关复杂度分析
4.1 暴力求解
-
时间复杂度
-
初始化tCharMap:首先遍历字符串t中的所有字符,这一步的时间复杂度为O(m),其中m是字符串t的长度。向HashMap中插入元素的平均时间复杂度为O(1),因此这一步的时间复杂度为O(m)。
-
寻找最小窗口:通过嵌套循环遍历字符串s,试图找到包含t中所有字符的最小窗口。对于s中的每一个字符(外层循环),它会迭代剩余的字符(内层循环)来找到这样的窗口。这导致了最坏情况下的时间复杂度为O(n^2),其中n是字符串s的长度。这是因为对于s中的每个字符,我们在最坏的情况下可能需要扫描它右侧的每个其他字符。
-
内层循环中的操作:内层循环中进行了检查tCharMapCopy中是否存在字符、更新映射和复制HashMap(tCharMapCopy = new HashMap<>(tCharMap))等操作。HashMap的复制操作是O(m),因为它必须复制原始映射中的所有条目。这个操作对于外层循环的每次迭代都会进行。对于s中的每个字符,检查和更新HashMap的平均时间复杂度是O(1)。
-
综合考虑这些操作,主导因素是嵌套循环结构,使得整体时间复杂度为O(n^2 × m)
-
空间复杂度
-
tCharMap的空间复杂度:这个HashMap存储了字符串t中每个字符及其出现的次数。因此,它的空间复杂度取决于t中不同字符的数量。在最坏的情况下,如果t中每个字符都不同,这个映射的空间复杂度是O(m),其中m是字符串t的长度。
-
tCharMapCopy的空间复杂度:在外层循环的每次迭代中,我们都创建了HashMap tCharMap的一个副本。尽管这些副本是依次创建的,而不是同时存在的,但每个副本的空间复杂度也是O(m),因为它包含了t中所有不同字符的一个完整映射。
-
结果字符串ret的空间复杂度:这取决于找到的最小窗口的大小。在最坏的情况下,如果整个s是最小窗口,那么这个字符串的空间复杂度为O(n),其中n是字符串s的长度。因此,总的空间复杂度是由这三部分组成的,即O(m) + O(m) + O(n) = O(m + n)。这表明空间复杂度与输入字符串s和t的长度线性相关,主要是因为需要存储字符及其出现次数的映射以及可能的最小窗口子串。总结来说,此代码的空间复杂度主要受到两个因素的影响:一是存储t字符及其频率的映射,二是在查找过程中创建的映射副本以及存储结果子串。
-
因此,空间复杂度为O(m + n)。
4.2 滑动窗口
-
时间复杂度
-
哈希表操作:哈希表的插入、删除和查找操作的平均时间复杂度为O(1)。因此,尽管在遍历字符串和调整窗口的过程中进行了多次这些操作,它们的时间复杂度在整个算法的上下文中是线性的。综合以上各点,整个算法的总时间复杂度为O(n + m),这反映了需要分别遍历字符串s和t各一次,而对哈希表的操作平均来说是常数时间的。
-
窗口内数据更新:虽然左指针left的移动看起来在内部循环中进行,但每个字符在整个算法中由左指针和右指针各访问一次,因此这部分操作的总时间复杂度仍然是O(n)。
-
遍历字符串s:算法通过移动右指针right来遍历字符串s一次,对于字符串s中的每个字符,可能需要进行一次哈希表的更新操作。这部分的时间复杂度为O(n),其中n是字符串s的长度。
-
初始化频率表:遍历字符串t以构建字符频率表的时间复杂度为O(m),其中m是字符串t的长度。
-
空间复杂度
-
答案记录:用于存储最小窗口的起始位置和长度的变量是固定大小的,可以忽略不计。因此,整个算法的总空间复杂度主要由哈希表决定,为O(m)。总结来说,优化后的滑动窗口算法的时间复杂度是O(n + m),空间复杂度是O(m),这反映了算法与输入字符串s的长度和字符串t中不同字符的数量线性相关。
-
频率表和窗口计数表:这两个哈希表存储了字符串t中所有唯一字符的计数,以及当前窗口中字符的计数。空间复杂度取决于字符串t中不同字符的数量。在最坏的情况下,如果t中每个字符都不同,这部分的空间复杂度为O(m),其中m是字符串t中唯一字符的数量。