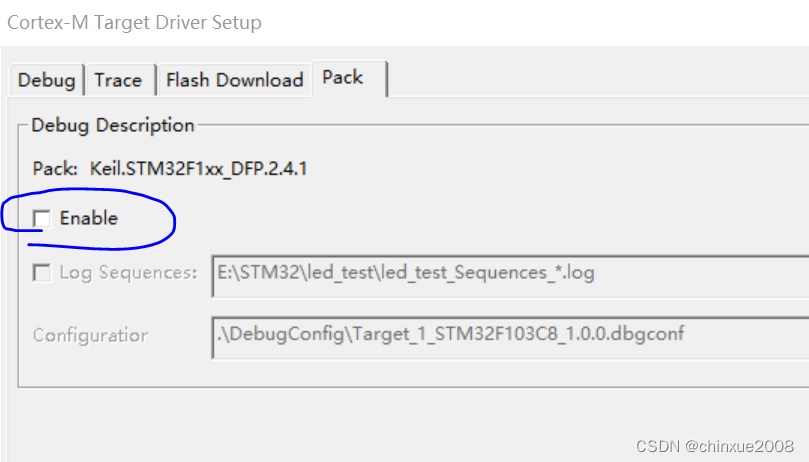
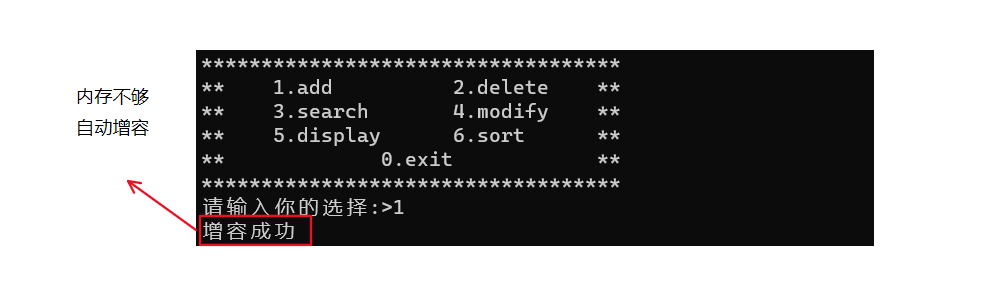
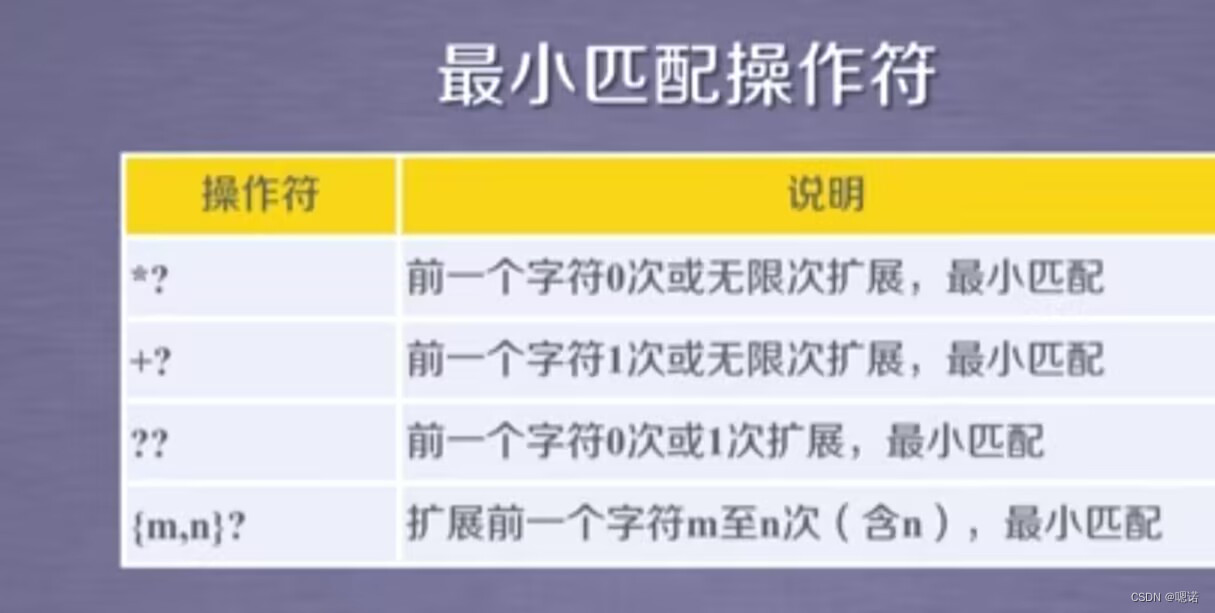
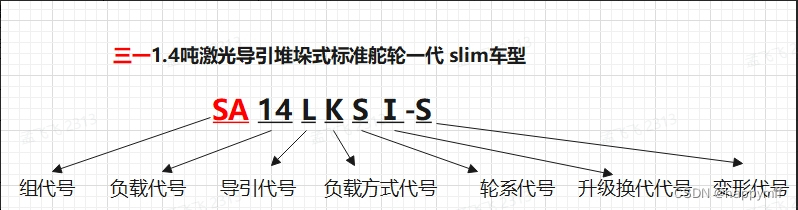
安装 SEED-XDS560v2 Driver.exe
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/473709.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
下一代Windows系统曝光:基于GPT-4V,Agent跨应用调度,代号UFO
下一代Windows操作系统提前曝光了??
微软首个为Windows而设的智能体(Agent) 亮相:
基于GPT-4V,一句话就可以在多个应用中无缝切换,完成复杂任务。整个过程无需人为干预,其执行成功…
生成式 AI - Diffusion 模型 (DDPM)原理解析(1)
来自 论文《 Denoising Diffusion Probabilistic Model》(DDPM) 论文链接:https://arxiv.org/abs/2006.11239 Hung-yi Lee 课件整理
简单地介绍diffusion model 的基本概念,diffusion model有很多不同的变形,现在比较…
让Python遇上Office--从编程入门到自动化办公实践
最近仔细的学习了这本《让Python遇上Office》的书,同时把我的学习进程与心得录制了同步视频。
到今天终于把全部90集完成,并且上传到下面的视频平台了,欢迎大家观看并指正!
西瓜视频:https://www.ixigua.com/7300628…
WEB APIs(2)
应用定时器可以写一个定时轮播图,如下
<!DOCTYPE html>
<html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport&qu…
【MySQL进阶之路】MySQL中到底为什么会出现幻读?
欢迎关注公众号(通过文章导读关注:【11来了】),及时收到 AI 前沿项目工具及新技术的推送! 在我后台回复 「资料」 可领取编程高频电子书! 在我后台回复「面试」可领取硬核面试笔记! 文章导读地址…
精通C语言:打造高效便捷的通讯录管理系统
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:C语言项目 贝蒂的主页:Betty‘s blog 引言 在我们大致学习完C语言之后,我们就可以利用目前所学的知识去…
【python】网络爬虫与信息提取--正则表达式
一、正则表达式 正则表达式是用来简洁表达一组字符串的表达式。是通用的字符串表达框架,简洁表达一组字符串的表达式,针对字符串表达“简洁”和“特征”思想的工具,判断某字符串的特征归属。 用处:表达文本类型的特征;…
Python爬虫之自动化测试Selenium#7
爬虫专栏:http://t.csdnimg.cn/WfCSx
前言
在前一章中,我们了解了 Ajax 的分析和抓取方式,这其实也是 JavaScript 动态渲染的页面的一种情形,通过直接分析 Ajax,我们仍然可以借助 requests 或 urllib 来实现数据爬取…
数学建模【非线性规划】
一、非线性规划简介
通过分析问题判断是用线性规划还是非线性规划
线性规划:模型中所有的变量都是一次方非线性规划:模型中至少一个变量是非线性
非线性规划在形式上与线性规划非常类似,但在数学上求解却困难很多
线性规划有通用的求解准…