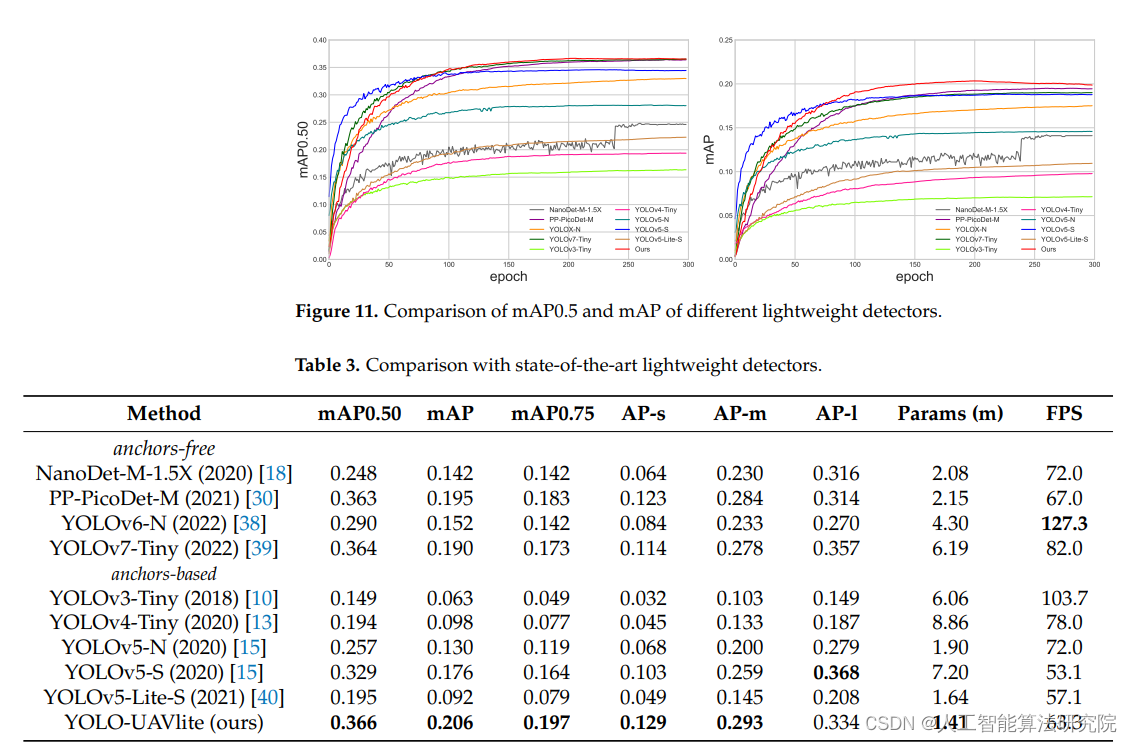
实验十二：微分方程模型
练习四
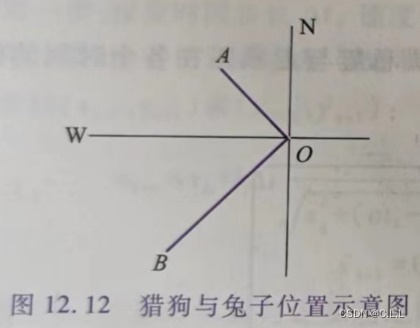
1.如图12.12所示,有一只猎狗在B点位置发现了一只兔子在正东北方距离它200m的地方0处,此时兔子开始以8m/s的速度向正西北方距离为120m的洞口A全速跑去,假设猎狗在追赶兔子的时候始终朝着兔子的方向全速奔跑,按要求完成下面的实验:
(1)问猎狗能追上兔子的最小速度是多少?
(2)选取猎狗的速度分别为15m/s,18m/s,计算猎狗追赶兔子时跑过的路程.
(3)画出猎狗追赶兔子奔跑的曲线图.
(4)假设在追逐过程中,当猎狗与兔子之间的距离为30m时,兔子由于害怕,随后奔跑的速度每秒减半,而猎狗却由于兴奋随后奔跑的速度每秒增加0.1倍,再按(1)-(3)完成实验任务.
最小速度即为兔子刚好到达洞口时，猎狗恰好追上的速度。设最小速度为v.
我们不妨以OA方向为y轴正方向，OB方向为x轴负方向建立直角坐标系。
设兔子在t时刻到达了（0,8t）点，而猎狗此刻位置为（x,y），猎狗在该时间内走的路程s.
可列出下列等式：
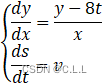
对上式关于x求导，得
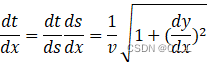
整理可得二阶微分方程的初值问题，（c为初始时猎狗的位置）
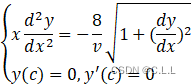
（1）
clc;clear;
syms y(x) v
m=x*diff(y,2)==-8/v*sqrt(1+(diff(y))^2);
Dy=diff(y);
y=dsolve(m,y(-200)==0,Dy(-200)==0);
y=matlabFunction(y);
v=solve(y(v,0)==120);
v=v(v>0)
v =(4*61^(1/2))/3 + 20/3
（2）
clc;clear;
syms y(x)
m=x*diff(y,2)==-8/15*sqrt(1+(diff(y))^2);
Dy=diff(y);
y=dsolve(m,y(-200)==0,Dy(-200)==0);
y=y(1);
y=matlabFunction(y);
y(0) %149.0683,大于120
f=@(x)y(x)-120;
fsolve(f,-5)% -2.7856 + 0.0000i,则猎狗未追上兔子
t=120/8*15
syms y(x)
m=x*diff(y,2)==-8/18*sqrt(1+(diff(y))^2);
Dy=diff(y);
y=dsolve(m,y(-200)==0,Dy(-200)==0);
y=y(1);
y=matlabFunction(y);
y(0) %110.77小于120
t=110.77/8*18
t=225
t = 249.2325
(3)以猎狗的速度为18为例；
clc;clear;
syms y(x)
m=x*diff(y,2)==-8/18*sqrt(1+(diff(y))^2);
Dy=diff(y);
y=dsolve(m,y(-200)==0,Dy(-200)==0);
y=y(1);
ezplot(y,[-200,0])
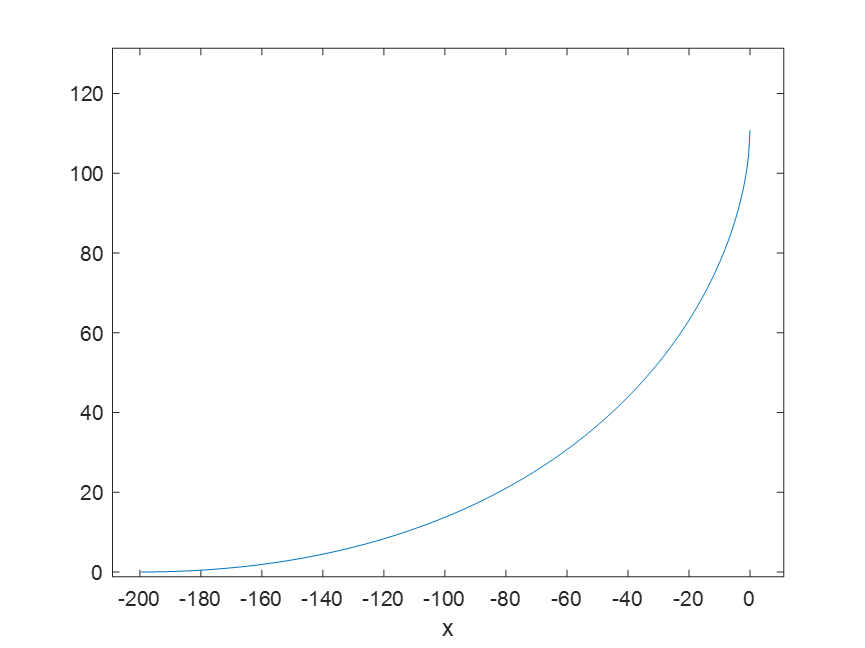
（4）能力有限，不写了
2.使用多种方法求解下述问题:在边长为a的正方形的四个顶点上各有一人,如图12.13所示, 在某一时刻,四人同时出发以匀速。按顺时针方向追赶下一个人,如果他们始终保持对准目标,试确定每个人的行进路线,计算每人跑过的路程和经历的时间.
能力有限，不写了 doge
3.有一段时间,某国原子能委员会是这样处理放射性废物的:他们把这些废物装人密封性能很好的圆桶中,然后扔到水深300ft(1ft=0.3048m,约91.44m)的海里,这种做法是否会造成放射性废物泄露污染,自然引起了许多生态学家及社会各界的关注.当时该国原子能委员会认为,用来封装放射性废物的圆桶非常坚固,投放到水深300的海里决不会破损而泄露放射性废物,因此总是认为这种做法是绝对安全的.但是一些工程技术人员却对此表示怀疑,他们认为圆桶在和海底相撞时有可能发生破裂.于是,在当时引起了一场争论.
已知当时该国封装放射性废物使用的是55gal(1gal=3.785L)的圆桶,装满核放射性废物后的重量为527.436lb(1lb=0.4536kg,约239.2450kg),经过多次实验测得圆桶在下沉时所受的浮力为f=2090.735N,阻力系数为c=0.08,圆桶碰撞发生破裂的直线极限速度是40ft/s(约12.192m/s).现在,在约定圆桶以直线方向往下沉的情况下,请你回答这种处理方法可靠吗?
4.如图12.14,有一半径为4a的大圆,里面有一个半径为a的小圆,现在,大圆固定而小圆在大圆内相切滚动,设起点M的坐标为(4a,0),确定小圆上一点M的轨迹曲线,并动态模拟内切小圆的滚动轨迹.
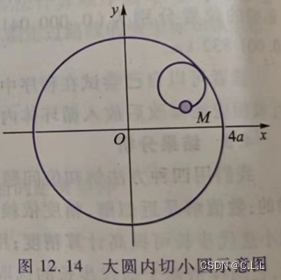
这个画出来是一个星形线，在实验三的练习二的第二题有相似题目。
不妨设a=1；
我们假设大圆内的小圆圆心顺时针旋转θ度，那么其圆心旋转后为（3cosθ，3sinθ）；而接触点为（4cosθ，4sinθ），而对应的M点在接触点顺时针旋转4θ后所在的位置，其坐标为（cos4θ^2-sin4θ^2+3cos4θ，2sin4θcos4θ+3sin4θ）
clc;clear;
t=0:0.01:2*pi;m=0:0.01:2*pi;
for i=1:length(t)x=cos(t(i))*cos(-4*t(i))-sin(t(i))*sin(-4*t(i))+3*cos(t(i));y=sin(t(i))*cos(-4*t(i))+cos(t(i))*sin(-4*t(i))+3*sin(t(i));hold onplot(x,y,'r.');getframe;
end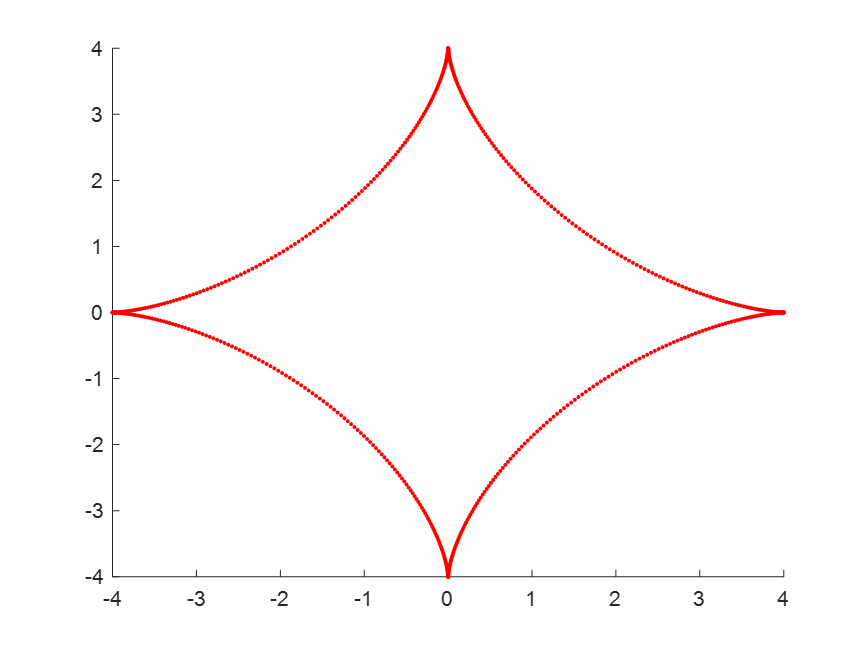 
5.一个人在平面上滑着曲线
以恒定的速率跑步,起点在(5，0)处,方向为逆时针,这时,他养的狗在坐标原点处以速率w跑向主人,狗的运动方向始终指向主人,选取不同的v和w,动态演示这个追逐过程。
设在时间t内，人运动的距离为5t，其所对应的圆心角为t，则其位置为（5cost，5sint）.
设狗运动到位置（xx,yy）.
我们可以根据速度的合成与分解列出一下式子：
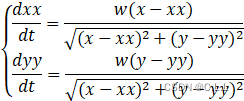
其中x=5cost，y=5sint.
clc;clear;w=2;v=5;
f=@(t,x)[w*(v*cos(t)-x(1))/sqrt((v*cos(t)-x(1))^2+(v*sin(t)-x(2))^2);w*(v*sin(t)-x(2))/sqrt((v*cos(t)-x(1))^2+(v*sin(t)-x(2))^2)];
[a,b]=ode45(f,[0,10],[0;0]);
for i=1:length(b(:,1))
plot(b(i,1),b(i,2),'r.');
hold on
ezplot('x^2+y^2-25');
hold on
plot(5*cos(a(i)),5*sin(a(i)),'*');
axis equal
axis off
hold off
getframe;
end
自我提醒：这里有几个问题需要注意：首先，微分方程组在用matlab解的时候首先选择dsolve函数，dsolve函数要求使用sym类型，所以我们要定义一个x(t)和y(t),比如说：
clc;clear;
syms x(t) y(t)
m=[2*diff(x)+diff(y)-y==exp(-t);diff(x)+x+y==0];
dsolve(m)
这里我试了一下x(1)和x(2)的形式，不行,我觉得这种形式主要使用在function类型中。只能用x和y这种。
其次，我们再使用ode类型，ode要求函数定义时使用function类型，function定义时我们可以用f=@（t,x）这种类型或者在另外一个文件新建一个函数function这种。（在本文档后面用function的话需要@函数名）；
例如：
clc;clear;
[t,y]=ode15s(@erjie,[0,3000],[2,0]);
plot(t,y(:,1),'-');
function f=erjie(t,y)
f=zeros(2,1);
f=[y(2);1000*(1-y(1)^2)*y(2)-y(1)];
end
另外注意使用f=@（t,x）时，一定注意x和t的顺序，(前者是关于谁的导数，后者是函数)不能搞反了，要不有时候也会报错。
推荐下一篇文章：
数学实验第三版（主编：李继成 赵小艳）课后练习答案（十三）（1）
https://blog.csdn.net/2301_80199493/article/details/136142085?spm=1001.2014.3001.5502
本文由作者自创，由于时间原因，难免出现些许错误，还请大家多多指正。创作不易，请大家多多支持。
