一、原题呈现

1、题目描述

有一个箱子容量为 V（正整数，0＜＝V＜＝20000），同时有 n 个物品（0＜n＜＝30），每个物品有一定的体积和价值。要求 n 个物品中，任取若干个装入箱内，在箱子能放得下的前提下，满足箱子内部的价值最大。

2、输入描述

一个整数 v，表示箱子容量
一个整数 n，表示有 n 个物品
接下来 n 个整数，分别表示这 n 个物品的各自体积和价值

3、输出描述

一个整数，表示箱子能装下的最大价值。

4、样例输入

3
2
2 100
4 200

5、样例输出

100

二、思路分析

这是一个最基础的01背包问题。

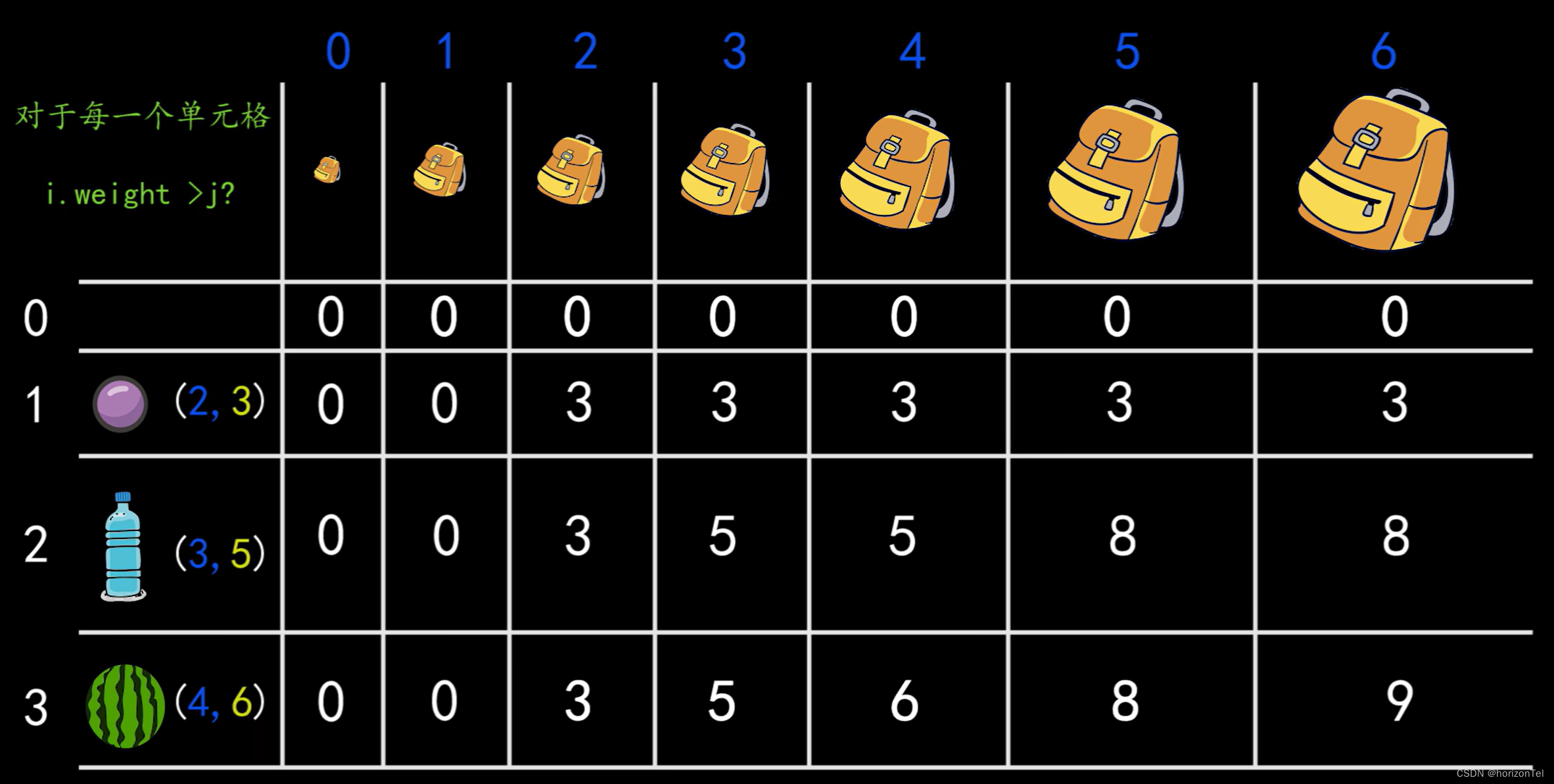
这里本人懒得画图，截取了某个大佬的图片来讲解
1、首先我们是按照行来进行遍历。
2、第0行和第0列全都设置为默认0，并且这个单元格的意思是可以选取i行以上的物品，并且背包大小为j，此时能够装到背包内物品价值的最大值
3、我们假设选取第二行第三列的位置，此时我们对于背包的处理有两种情况
（1）不装入物品，那么re[i][j] = re[i - 1][j]
（2）装入该行的物品，那么留给前面的背包质量就为j - weight[i]，因此我们可以定位到第i-1行，j - weight[i]列的re值，加上新放入的物品的价值就为re[i][j]的值，即re[i][j] = re[i - 1][j - weight[i]] + value[i]
4、我们将上面两种情况进行求最大值，就是当前re[i][j]的值
5、特殊情况：如果当前背包装不下这个物品（即j - weight[i] < 0），那么我们就直接继承上一行这一列值，即re[i][j] = re[i - 1][j]

三、整体代码

#include<iostream>
#include<math.h>
#include<algorithm> 
using namespace std;int main() {int v, n, i, j;while(cin>>v>>n) {int re[35][21000] = {0};int weight[40], value[40];for(i = 1; i <=n; i++)cin>>weight[i]>>value[i];for(i = 1; i <= n; i++) {for(j = 1; j <= v; j++) {if(j - weight[i] < 0)re[i][j] = re[i - 1][j];else {re[i][j] = max(re[i - 1][j], re[i - 1][j - weight[i]] + value[i]);}}}cout<<re[n][v]<<endl;}return 0;
}