目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1 SFLA的基本原理
4.2 神经网络优化
5.完整程序
1.程序功能描述
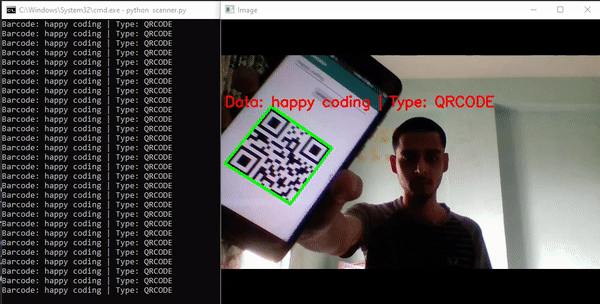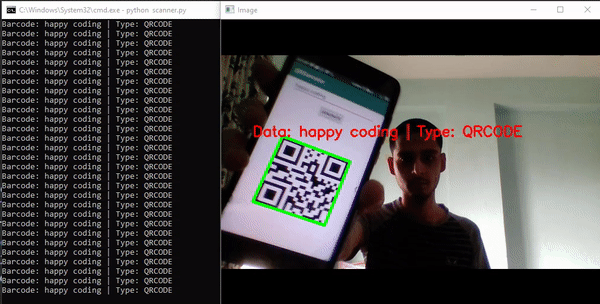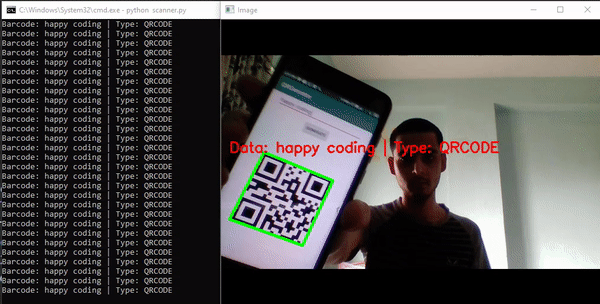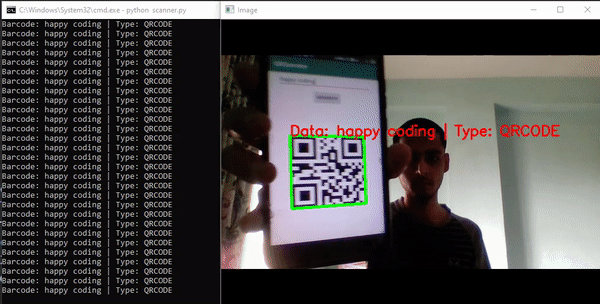
基于SFLA算法的神经网络优化。通过混合蛙跳算法,对神经网络的训练进行优化,优化目标位神经网络的训练误差,通过优化,使得训练误差越来越小,从而完成神经网络权值的优化。
2.测试软件版本以及运行结果展示
MATLAB2022a版本运行
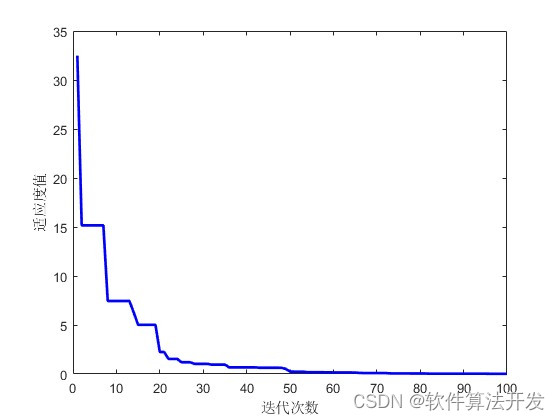
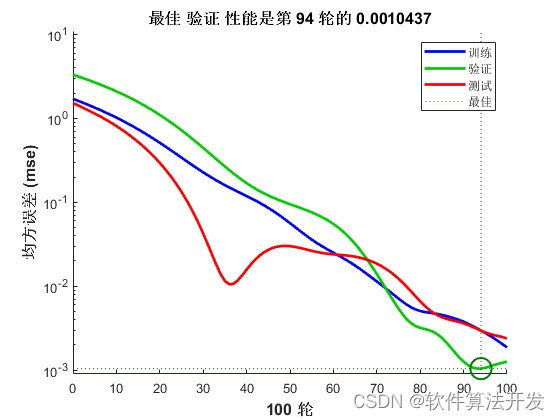


3.核心程序
.....................................................................
% 定义神经元数量
Nnet = 12;
% 创建一个前馈神经网络,训练函数为'traingdx'
NET = feedforwardnet(Nnet,'traingdx');
% 使用Pin作为输入,Pout作为目标来训练神经网络,训练结果存储在tr中
[NET,~] = train(NET,Pin,Pout);
% 计算神经网络的性能
Performace = perform(NET,Pin,Pout);
%定义目标函数
jobs = @(x) func_mse(x,NET,Pin,Pout);%SFLA算法% 优化后的权重和偏置存储在x中,误差存储在err_ga中
[x, ~] = func_sfla(jobs, RC*Nnet+Nnet+Nnet+1);
%优化后的网络,使用优化后的权重和偏置更新神经网络
NET = setwb(NET, x');% 计算优化后的神经网络误差
Outputs=NET(Pin);
TestOutputs=NET(Tin);err1=Pout-Outputs;
err2=Tout-TestOutputs;figure;
subplot(2,2,1)
plot(Pout,'b');
hold on;
plot(Outputs,'r');
legend('训练集的真实值','训练集的预测值');subplot(2,2,2)
plot(Tout,'b');
hold on;
plot(TestOutputs,'r');
legend('测试集的真实值','测试集的预测值');subplot(2,2,3)
plot(err1,'linewidth',2);
legend('训练集误差');
ylim([-0.5,0.5]);subplot(2,2,4)
plot(err2,'linewidth',2);
legend('测试集误差');
ylim([-0.5,0.5]);figure;
subplot(1,2,1)
[yfits,gof] = fit(Pout',Outputs','poly3');
plot(Pout',Outputs','o');
hold on
plot(yfits,'k-','predobs');
xlabel('真实值');
ylabel('预测输出值'); subplot(1,2,2)
[yfits,gof] = fit(Tout',TestOutputs','poly3');
plot(Tout',TestOutputs','o');
hold on
plot(yfits,'r-','predobs');
xlabel('真实值');
ylabel('预测输出值');
294.本算法原理
神经网络优化是一个复杂的问题,通常涉及到权重和偏置的调整,以便最小化训练误差。SFLA是一种启发式搜索算法,它结合了蛙跳算法和遗传算法的特点,用于求解全局优化问题。在神经网络优化中,SFLA可以用于寻找最优的权重和偏置,从而改善网络的性能。
4.1 SFLA的基本原理
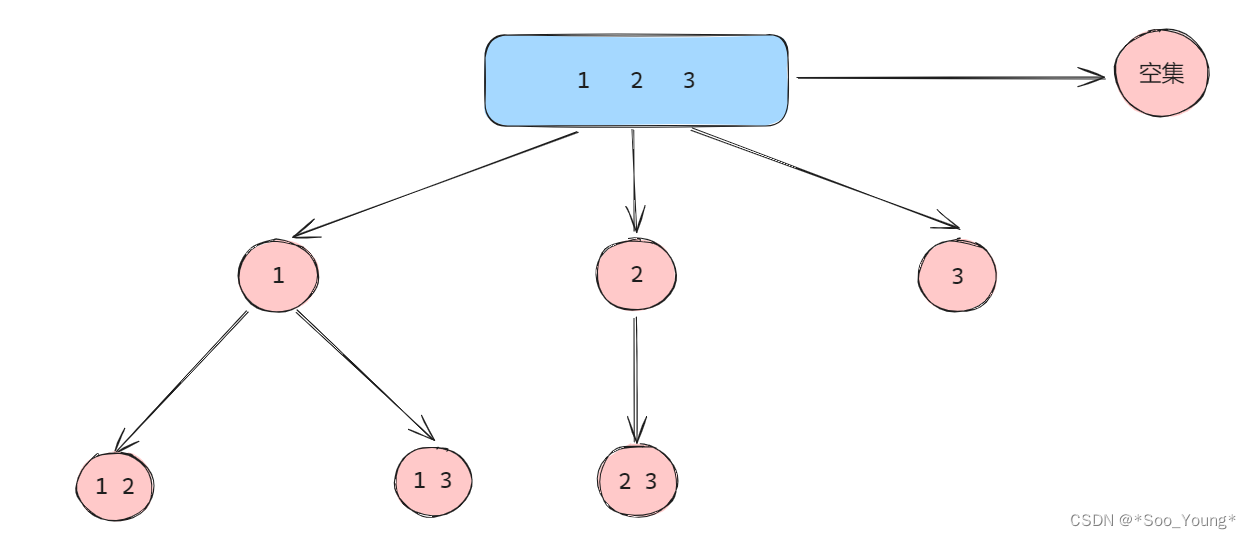
SFLA的基本原理是将搜索空间中的解(即神经网络的权重和偏置)视为“蛙群”。算法通过模拟蛙群的跳跃行为来搜索解空间,寻找最优解。
- 初始化:随机生成一组初始解(蛙群),每个解代表神经网络的一组权重和偏置。
- 分组:将蛙群按照适应度(如训练误差)排序,并分成若干个子群。
- 局部搜索:在每个子群内,进行蛙跳操作,即根据一定的规则和步长更新解的位置(权重和偏置)。
- 全局信息交流:定期将各个子群的最优解进行交换,以促进全局搜索。
- 迭代:重复上述步骤,直到满足停止准则(如达到最大迭代次数或解的质量不再显著提高)。
4.2 神经网络优化

通过SFLA算法对神经网络参数进行全局优化,可以有效地探索参数空间并找到更优的神经网络结构配置,从而提高模型的预测性能。
基于SFLA的神经网络优化是一种有效的全局优化方法。它通过模拟蛙群的跳跃行为来搜索解空间,结合局部搜索和全局信息交流的策略,能够在复杂的搜索空间中找到近似最优解。然而,为了获得更好的性能,可能需要对SFLA的参数(如子群大小、跳跃步长等)进行仔细调整。此外,与其他优化算法(如遗传算法、粒子群优化等)的结合也是值得研究的方向。
5.完整程序
VVV