LeetCode 104.二叉树的最大深度

题目链接：104.二叉树的最大深度
文章讲解：代码随想录#104.二叉树的最大深度
视频讲解：104.二叉树的最大深度

题目描述

给定一个二叉树 root ，返回其最大深度
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例1

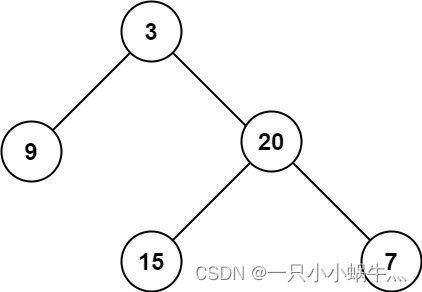
输入：root = [3,9,20,null,null,15,7]
输出：3

示例2

输入：root = [1,null,2]
输出：2

提示

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

思路

什么是二叉树节点的高度？么是二叉树节点的深度？

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
  使用前序求的就是深度，使用后序求的是高度
  根节点的高度就是二叉树的最大深度，所以可以通过后序遍历来求二叉树的最大深度。

递归后序遍历参考代码

#define MAX(a, b) (a) > (b) ? (a) : (b)
// 使用后序遍历计算二叉树的高度，二叉树的最大深度也就是根节点到叶子节点的高度
int treeDepth(struct TreeNode *node)
{if (node == NULL) {return 0;}int lDepth = treeDepth(node->left); // 左int rDepth = treeDepth(node->right); // 右int depth = MAX(lDepth, rDepth); // 中return depth + 1;}
int maxDepth(struct TreeNode* root) {return treeDepth(root);
}

递归前序遍历参考代码

int res;// 使用前序遍历计算二叉树的最大深度，必须需要一个变量来记录当前遍历的depth
void treeDepth(struct TreeNode *node, int depth)
{res = res > depth ? res : depth;  // 中if (node->left == NULL && node->right == NULL) {return ;}if (node->left != NULL) { // 左depth++;treeDepth(node->left, depth);depth--; // 回溯}if (node->right != NULL) { // 右depth++;treeDepth(node->right, depth);depth--; // 回溯}return;
}int maxDepth(struct TreeNode* root) {res = 0;if (root == NULL) {return res;}treeDepth(root, 1);return res;
}

总结

1. 递归相对简单一些，后面有时间了深度用层序遍历解决这道题

---

LeetCode 111.二叉树的最小深度

题目链接：111.二叉树的最小深度
文章讲解：代码随想录#111.二叉树的最小深度
视频讲解：LeetCode：111.二叉树的最小深度

题目描述

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

示例1

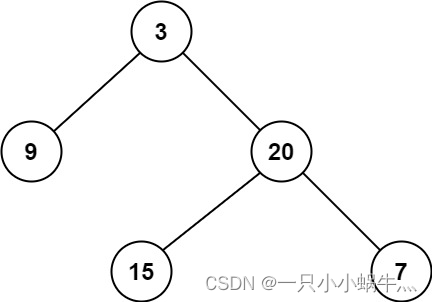
输入：root = [3,9,20,null,null,15,7]
输出：2

示例2

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

思路

这道题关键点是要计算从根节点到最近叶子节点的最短路径上的节点数量。
需要注意的是如果左子树为空，右子树不为空，则最小深度为1+右子树的深度。同样，如果右子树为空，左子树不为空，则最小深度为1+左子树的深度。

参考代码

int minDepth(struct TreeNode* root) {if (root == NULL) {return 0;}int lDepth = minDepth(root->left); // 左int rDepth = minDepth(root->right); // 右if (root->left == NULL && root->right != NULL) { // 处理中节点return 1 + rDepth;}if (root->left != NULL && root->right == NULL) {return 1 + lDepth;}int depth = lDepth > rDepth ? rDepth : lDepth; // 中return 1 + depth;
}

---

LeetCode 222.完全二叉树的节点个数

题目链接：222.完全二叉树的节点个数
文章讲解：代码随想录#222.完全二叉树的节点个数
视频讲解：要理解普通二叉树和完全二叉树的区别！ | LeetCode：222.完全二叉树节点的数量

题目描述

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例1

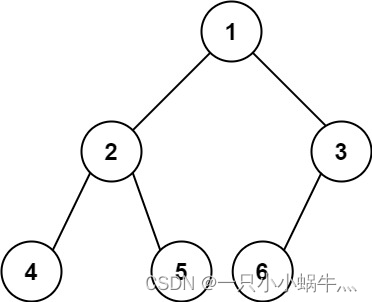
输入：root = [1,2,3,4,5,6]
输出：6

示例2

输入：root = []
输出：0

示例 3

root = [1]
1

提示

• 树中节点的数目范围是[0, 5 * 10^4]
• 0 <= Node.val <= 5 * 10^4
• 题目数据保证输入的树是 完全二叉树

思路

第一反应就是深度遍历或层序遍历所有的节点，时间复杂度为O(n)。
但这不是最优解，理解完全二叉树的特点后，会有更好的解决方案。
在完全二叉树中，除了最底层节点可能没有填充满以外，其余层的是一个满二叉树，而且最底层的节点都集中在最左边。
如果最底层为n层，则该层包含的节点数为[1, 2^(n-1)]，除最底层以外的节点数为2^(n-1)-1。
对于一个完全二叉树，分别递归左孩子和右孩子，递归到某一深度一定会有左孩子或右孩子是满二叉树，如果是满二叉树可以根据深度k计算节点数为2^k-1。

具体思路可以参考代码随想录。

后序遍历参考代码1

int countNodes(struct TreeNode* root) {if (root == NULL) {return 0;}int lcnt = countNodes(root->left);int rcnt = countNodes(root->right);return 1 + lcnt + rcnt;    
}

后序遍历参考代码2

// 根据完全二叉树特性
int countNodes(struct TreeNode* root) {if (root == NULL) {return 0;}int lcnt = 0, rcnt = 0;struct TreeNode* lnode = root->left;struct TreeNode* rnode = root->right;while (lnode) {lnode = lnode->left;lcnt++;}while (rnode) {rnode = rnode->right;rcnt++;}if (lcnt == rcnt) {return (2 << lcnt) - 1;}return 1 +  countNodes(root->left) + countNodes(root->right);
}