递归算法
直接或间接的调用自身的算法称为递归函数,采用栈结构,先调用的最后返回。
主要形式就是先纵后横,一个分支走到底,再退回一个到兄弟节点,依次回退。
列出递归的三种形式:切蛋糕、递推公式、等价转换。
递归要素:
- 明确递归得到结果是什么
- 提取重复的逻辑,缩小问题的规模不断递去(大部分问题由大向小递归)
- 变化的参数
- 明确递归的终止条件
阶乘函数:
- 明问题:jiecheng(n) 返回n!
- 找重复:n!=n*(n-1)!=n*(n-1)*(n-2)!=.....
- 找变化:变化的量为参数
- 找边界:边界时n=0时,返回1
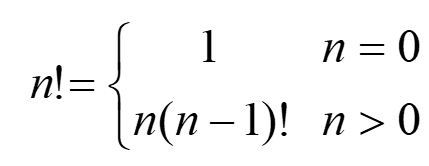
public int jiecheng(int n){if (n == 1){return 1;//递归出口}else return n * jiecheng(n-1);//递归方程,从大到小}字符串的翻转
- 明问题:recerse(s) 返回s的翻转字符
- 找重复:字符串的翻转等于最后一个字符+前n-1个字符的翻转....
- 找变化:变化的量为字符串的长度,作为参数
- 找边界:边界时长度为0时结束。
public static String reverse(String s,int n){if (n==0) return "";return s.charAt(n-1)+reverse(s,n-1);}斐波那契数列(Fibonacci数列)
- 明问题:Fibonacci(n) 返回n对应的斐波那契数
- 找重复:n的斐波等于n-1的斐波+n-2的斐波
- 找变化:变化的量为参数
- 找边界:边界时n=1 || 2时,返回1
无穷数列1,1,2,3,5,8,13,21,34,55,……,称为Fibonacci数列。
斐波那契数列的分段函数(递归函数)为:
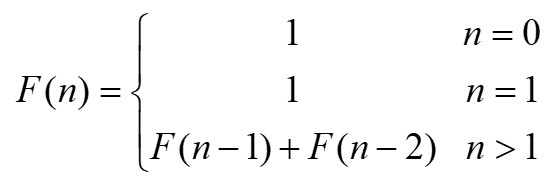
public int fibonacci(int n){if (n == 1 || n == 2){return 1;//递归结束位置}else return fibonacci(n-1) + fibonacci(n-2);//递归函数}最大公约数

- 明问题:辗转相除的m%n
- 找重复:m与n的最大公约数由n与m%n的最大公约数决定...依次类推
- 找变化:变化的量为m,n的取值。
- 找边界:边界时m%n==0时,返回n
public static int gcb(int m,int n){if (m%n==0) return n;return gcb(n,m%n);}指数运算的改进
求:
基本思想改变底数与指数,将底数变为原来的平方,则相应的指数变为原来的二倍。

private static int pow0(int a,int n) {if (n==0) return 1;int res=a;//底数int ex=1;//指数while(ex*ex<n){//ex*ex来判断下一层的res*res是否超过a的n次幂res=res*res;//改变底数ex*=2;//改变指数}return res*pow0(a,n-ex);//递归思想,递归剩余部分,不是2的倍数}上楼梯问题
一共有n层楼梯,每次只能上1层或2层或3层,问一共有几种上楼的方法。
- 明问题:walker(n) 返回n层楼梯的走法
- 找重复:若第一次上1层,则变成求剩余n-1层有几种走法问题;若第一次上2层,则变成求剩余n-2层有几种走法问题;若第一次上3层,则变成求剩余n-3层有几种走法问题;
- 找变化:楼梯的层数在发生变化
- 找边界:当楼梯只有1层或2层或3层时分别有1种,2种,4种走法
private static int walker(int n) {//此函数返回上n层楼梯所需的时间if (n==0) return 0;if (n==1) return 1;if (n==2) return 2;if (n==3) return 4;return walker(n-1)+walker(n-2)+walker(n-3);}递归排序
- 明问题:sort(nums,n)返回0~n排好序的数组
- 找重复:对n个元素排序可以看作最后一个元素插入对前n-1个元素的排序
- 找变化:变化的量为排序的边界值的取值。
- 找边界:边界时n==0时结束
public static void sort(int []nums,int n){//n表示最后一个元素的索引if (n==0) return;sort(nums,n-1);int t=nums[n];int i=n-1;for (;i>=0;i--){if (nums[i]<=t) break;nums[i+1]=nums[i];//数组的插入操作}nums[i+1]=t;//最终空下来的位置时i+1}瓷砖铺放问题
有⼀长度为N(1<=N<=10)的地板,给定两种不同瓷砖:⼀种长度为1,另⼀种长度为2,数⽬不限。要将这个长度为N的地板铺满,⼀共有多少种不同的铺法?
一共有n块砖,第一次铺两块就还剩f(N-2),第一次铺一块就还剩f(n-1)

public int cizhuan(int n){if (n == 1){return 1;}if (n == 2){return 2;}return cizhuan(n-1) + cizhuan(n - 2);}整数划分问题
将正整数n表示成一系列正整数之和:n=n1+n2+…+nk,其中n1≥n2≥…≥nk≥1,k≥1。正整数n的这种表示称为正整数n的划分。求正整数n的不同划分个数。