1 IQR（Interquartile Range）四分位距的含义

官方定义： 四分位距（interquartile range, IQR），又称四分差。是描述统计学中的一种方法，以确定第三四分位数和第一四分位数的差距。与方差、标准差一样，表示统计资料中各变量分散情形，但四分差更多为一种稳健统计。

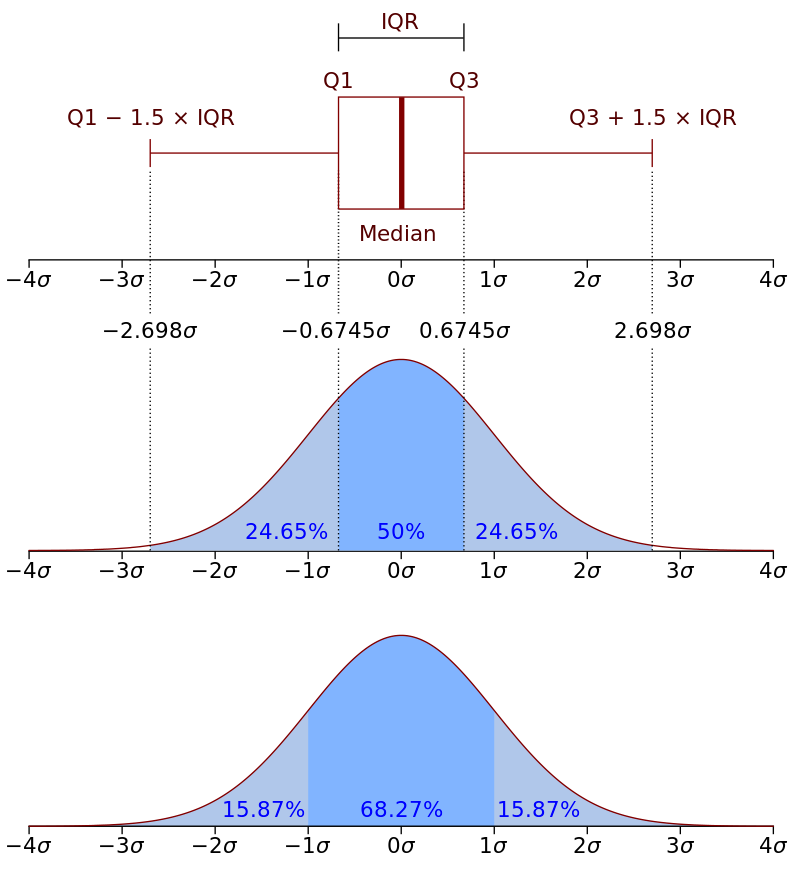
盒须图使用四分位数（将数据划分为大小相等的四组点）来绘制数据的形状。盒子代表第 1 个和第 3 个四分位数，它们等于第 25 个和第 75 个百分点。盒子内的线代表第二个四分位数，即中间值。

四分位距（该离群值检测方法正是因此而得名）是第一个和第三个四分位数（盒子边缘）之间的间距。Tukey 认为，如果数据点比第一个四分位数低 1.5 乘 IQR，或比第三个四分位数高 1.5 乘 IQR，就属于离群或极度离群。在经典的盒须图中，须线一直延伸到界限内的最后一个数据点。

四分位距 (IQR) 是一种衡量变异性的方法，它通过将数据集划分为四分位数来实现。四分位数将一个按等级排序的数据集划分为四个相等的部分。即 Q1（第 1 个四分位数）、Q2（第 2 个四分位数）和 Q3（第 3 个四分位数）。IQR 定义为 Q3–Q1，位于 Q3+1.5IQR 或 Q1-1.5IQR 之外的数据被视为离群值。

2 如何计算IQR

计算 IQR：分步指南 要计算四分位距，请按照下列步骤操作：

第 1 步：按升序排列数据首先按升序排列数据集。
第 2 步：求中位数Q2确定数据集的中位数，即中间值。 如果数据集有奇数个值，则中位数是中间的值。 对于偶数个值，取中间两个值的平均值。
步骤 3：找到下半部分 (Q1) 的中位数 确定数据集下半部分的中位数，排除总体中位数。 这是第一个四分位数 (Q1)。
步骤 4：找到上半部分的中位数 (Q3) 同样，找到数据集上半部分的中位数，排除整体中位数。 这是第三个四分位数 (Q3)。
第 5 步：**计算 IQR **最后，从 Q1 中减去 Q3，即可得到四分位数间距：IQR = Q3 – Q1。

举例说明：图表中的数据：

数列	参数	四分差
1	102
2	104
3	105	Q1
4	107
5	108
6	109	Q2（中位数）
7	110
8	112
9	115	Q3
10	118
11	118

从这个图示中，我们可以算出四分差的距离为115−105=10

用python代码实现：
用python实现当然可以一个一个循环去计算，但是python的numpy库提供了非常好用的封装函数，这里就不再去一个一个计算了，而是直接使用numpy库进行处理了，实现代码如下

import numpy as npdef get_iqr_data(datas):q1=np.quantile(datas,0.25)q2=np.median(datas)q3=np.quantile(datas,0.75)iqr=q3-q1down=q1-1.5*iqrup=q3+1.5*iqrreturn [q1,q2,q3,iqr,down,up]if __name__=="__main__":x=[1,2,3,4,5,6,7,8,9,10,11]rs=get_iqr_data(x)print(rs)

执行结果如下：

[3.5, 6.0, 8.5, 5.0, -4.0, 16.0]

通过这里的执行结果可以看住，在数据列表 [1,2,3,4,5,6,7,8,9,10,11] 中，四分之一的点的数据为3.5，这是因为总共11个数，四分之一落在了两个数之间，四分之二的点恰好就是第6个数了，四分之三的点又落在了两个数据之间，所以是8.5，那么这里IQR就是q3-q1即5.0，通过公式计算此时有效范围为(-4.0,16.0)，超出此范围的数据为无效数据。

参考：

https://blog.csdn.net/redrose2100/article/details/130211842
https://zh.wikipedia.org/wiki/%E5%9B%9B%E5%88%86%E4%BD%8D%E8%B7%9D