Problem: 773. 滑动谜题

题目描述

思路

由于题目提到最小步数，则可以使用BFS来穷举出最小的结果

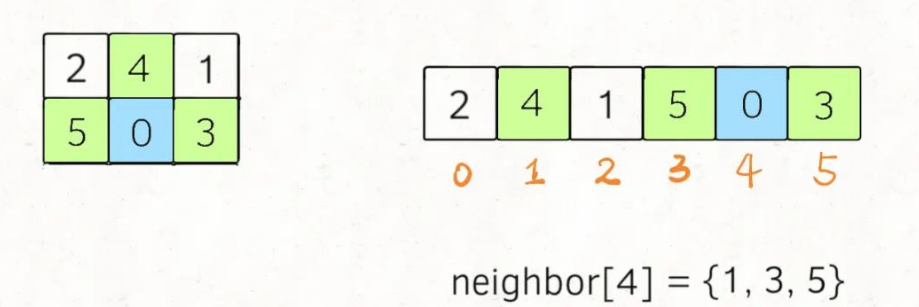
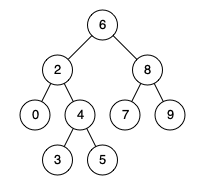
1.转换为BFS问题：由于0代表空着的可以移动的位置，所以我们只需要从当前位置和0的相邻位置移动从而转换出其它的可能的状态（这样也在逻辑上构成了一棵多叉树）
2.压缩二维数组，并标记出相邻索引：我们可以将二维数组board压缩，当在BFS遍历查找时找到一种状态等于压缩后的情况时，我们则立即返回此时的步数；但是我们为了解决相邻索引的问题，需要直接将这个映射写出来：在一维字符串中，索引i在二维数组中的的相邻索引为neighbor[i]；

解题方法

1.将题目所给的初始board压缩为字符串；
2.记录一维字符串的相邻索引(如下代码；按顺势针)；
3.BFS框架书写：

3.1.用一个无序表记录已经走过的状态（防止重复甚至出现死循环）；
3.2每次取出当前的状态，并匹配是否和目标target一致，一致则返回所需的步数（步数用一个变量step记录）；
3.3.每次找到当前数字0的索引并与其相邻的数字交换位置，同时要在无序表中判断是否已经存在；

复杂度

时间复杂度:

$O(n)$

空间复杂度:

$O(n)$

Code

class Solution {
public:/*** BFS* * @param board Given array* @return int*/int slidingPuzzle(vector<vector<int>> &board) {int row = 2;int col = 3;string start = "";string target = "123450";// Converts the 2x3 array to a stringfor (int i = 0; i < row; ++i) {for (int j = 0; j < col; ++j) {start.push_back(board[i][j] + '0');}}// Records the adjacent index of a one-dimensional stringvector<vector<int>> neighbor = {{1, 3},{0, 4, 2},{1, 5},{0, 4},{3, 1, 5},{4, 2}};//BFSqueue <string> q;unordered_set<string> visited;q.push(start);visited.insert(start);int step = 0;while (!q.empty()) {int sz = q.size();for (int i = 0; i < sz; ++i) {string cur = q.front();q.pop();// Determine whether the target situation has been reachedif (target == cur) {return step;}// Find the index of the number 0int index = 0;for (; cur[index] != '0'; ++index);// Switch the position of the digit 0 or any adjacent digitfor (int adj: neighbor[index]) {string new_board = cur;swap(new_board[adj], new_board[index]);// Prevent backtrackingif (!visited.count(new_board)) {q.push(new_board);visited.insert(new_board);}}}step++;}return -1;}
};