备战蓝桥杯---动态规划（入门3之子串问题）-编程知识

备战蓝桥杯---动态规划（入门3之子串问题）

本专题再介绍几种经典的字串问题。

这是一个两个不重叠字串和的问题，我们只要去枚举分界点c即可，我们不妨让c作为右区间的左边界，然后求[1,c)上的单个字串和并用max数组维护。对于右边，我们只要反向求单个字串和然后选左边界为c的一组即可。

下面是AC代码：

#include<stdio.h>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
long long t,a[50010],b[50010],max1[50010],n,ck[50010],hh;
int main(){scanf("%lld",&t);while(t--){memset(a,0,sizeof(a));memset(b,0,sizeof(b));memset(max1,0,sizeof(max1));scanf("%lld",&n);for(int i=1;i<=n;i++) scanf("%lld",&ck[i]);for(int i=1;i<=n;i++){if(i==1){a[i]=ck[i];max1[i]=ck[i];}else{a[i]=max(ck[i],ck[i]+a[i-1]);max1[i]=max(max1[i-1],a[i]);}}for(int i=n;i>=1;i--){if(i==n) b[i]=ck[i];else b[i]=max(ck[i],ck[i]+b[i+1]);}hh=-0x3f;for(int c=2;c<=n;c++){hh=max(hh,max1[c-1]+b[c]);}printf("%lld\n",hh);}
}

接下来，我们加点难度：

现在2变成了m，我们进行升维操作，我们令f[i][j]为前j个数（第j个数必须取）组成的i个不相交子段最大和。

当我们要从j-->j+1时，对于第j+1,它可以作为最后一个子段的末尾，也可以不做末尾而是起点，而此时我们要去得到i-1个不相交子段的max,因此，我们易得转移方程为：

f[i][j]=max(f[i][j-1]+a[j],f[i-1][k]+a[j])

复杂度为o(n^2*m)

我们考虑优化一下：

f[i][j]=a[j]+max(f[i][j-1],f[i-1][k]).

我们只要维护每一个点对应的一列上从上到下的max即可。

至于初始条件，0组的情况都为0（就比如m=1,有一种情况就是只选他自己，因此要赋0）

下面是AC代码（dp数组用滚动即可）：

#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000100],mmm;
int ans,dp[1000100];
int ck[1000100];
int main(){while(scanf("%d%d",&m,&n)!=EOF){ans=-0x3f;for(int i=1;i<=n;i++) scanf("%d",&a[i]);memset(dp,0,sizeof(dp));memset(ck,0,sizeof(ck));for(int i=1;i<=m;i++){mmm=-0x3f;for(int j=i;j<=n;j++){dp[j]=max(dp[j-1],ck[j-1])+a[j];ck[j-1]=mmm;mmm=max(mmm,dp[j]);}}printf("%d\n",mmm);	}
}

让我们再加点难度：如果是环状呢？

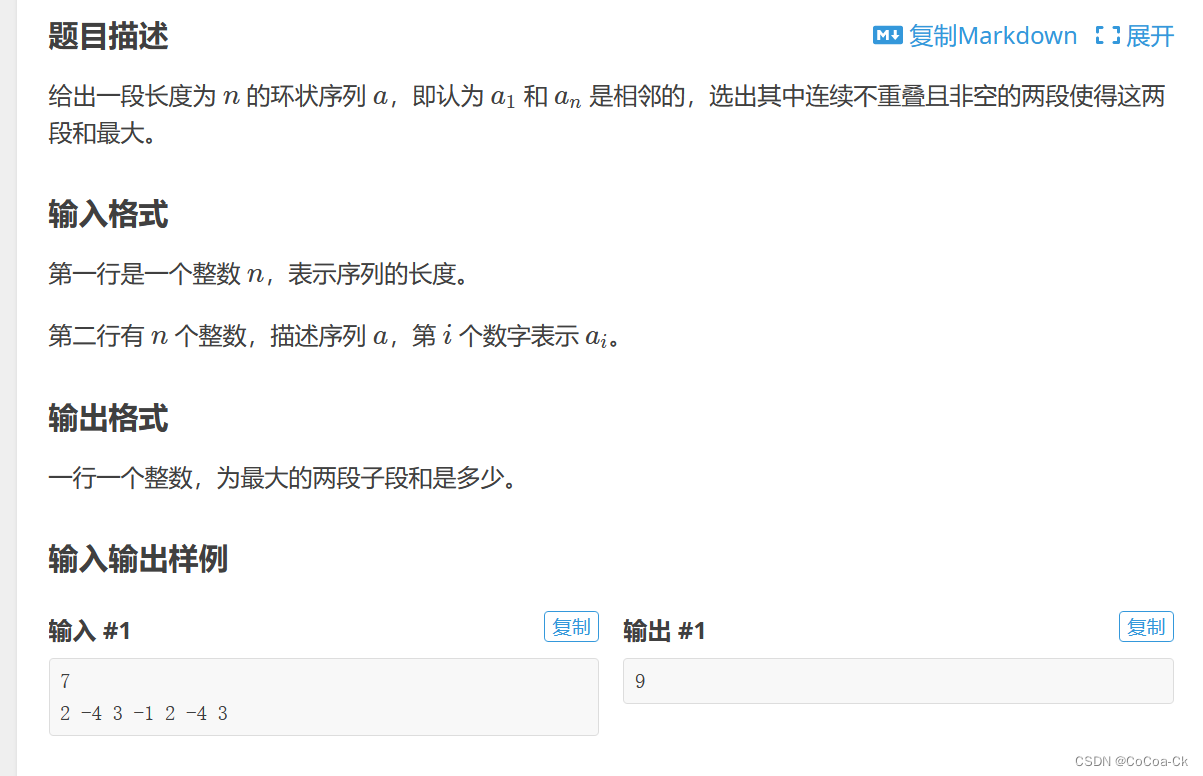
有一道石子合并的通过复制一份来解决，但是因为这个不能利用上一次划分的情况，换句话说，这一次每次断开都要重新求（原因在于不是区间dp)，于是我们不妨想一想另一种方法：

我们知道假如n与1没有被当成一段取，跟上面的就一样了。

如果n与1被当成一段取，那么我们在n与1断开的时候就相当于要求m+1段区间，其中第一段必须包含第一个元素，最后一个必须包含最后一个元素。

下面是AC代码（呜呜呜，直接初值赋了-0x3f，结果当成16进制，检查了好久）：

#include<bits/stdc++.h>
using namespace std;
int n,m,a[200100],mmm,mmm1;
int ans,dp[200100],dp1[200100];
int ck[200100],ck1[200100],hou[200100],maxx[200100];
int main(){scanf("%d",&n);ck1[0]=-10000000;ans=-10000000;for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) dp1[i]=a[i]+dp1[i-1];for(int i=1;i<=n;i++) ck1[i]=max(dp1[i],ck1[i-1]);for(int i=n;i>=1;i--) hou[i]=a[i]+hou[i+1];for(int i=n;i>=1;i--){if(i==n) maxx[i]=a[i];else maxx[i]=max(maxx[i+1],hou[i]);}for(int i=1;i<=2;i++){mmm=-10000000;for(int j=i;j<=n;j++){dp[j]=max(dp[j-1],ck[j-1])+a[j];ck[j-1]=mmm;mmm=max(mmm,dp[j]);}}mmm1=-10000000;for(int j=2;j<=n;j++){dp1[j]=max(dp1[j-1],ck1[j-1])+a[j];ck1[j-1]=mmm1;mmm1=max(mmm1,dp1[j]);}for(int i=2;i<=n-1;i++){ans=max(ans,dp1[i]+maxx[i+1]);}printf("%d\n",max(mmm,ans));	}

接下来，让我们再看看公共子序列问题吧：