虽说是div4,不过题目还是挺有东西的,而且难度不是特别高,题目出的很好
C是预处理前缀和,D是个位运算(位掩码),E题是个优美的数学题,F题是个爆搜,不过这个爆搜不是很裸,F是树上DP。
A Vlad and the Best of Five
思路:
记录一下AB出现的次数然后比较一下即可。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
using namespace std;int T;int main(){cin>>T;while(T--){string s;cin>>s;map<char,int> mp;for(auto x:s)mp[x]++;if(mp['A']>mp['B'])puts("A");else puts("B");}return 0;
}
B. Vlad and Shapes
题意:
弗拉迪斯拉夫有一个由 n × n n \times n n×n 单元组成的二进制正方形网格。网格上画有三角形或正方形,符号为 1 \texttt{1} 1 。由于他忙于耍酷,他要求您告诉他网格上画的是哪个形状。
- 三角形是由 k k k ( k > 1 k\gt1 k>1 )个连续的行组成的形状,其中第 i i i 行有 2 ⋅ i − 1 2 \cdot i-1 2⋅i−1 个连续的字符 1 \texttt{1} 1 ,中心的1位于一列。倒三角形也被视为有效三角形(但不能旋转 90 度)。
 左侧两幅图包含三角形的示例: k = 4 k=4 k=4 , k = 3 k=3 k=3 .右边两幅图片不包含三角形。
左侧两幅图包含三角形的示例: k = 4 k=4 k=4 , k = 3 k=3 k=3 .右边两幅图片不包含三角形。
- 正方形是由 k k k( k > 1 k>1 k>1 )个连续的行,其中第 i i i 行有 k k k 个连续的字符 1 \texttt{1} 1 ,这些字符与网格左边缘的距离相等。

两个方格的示例: k = 2 k=2 k=2 , k = 4 k=4 k=4 .
对于给定的网格,请确定在网格上绘制的图形类型。
思路:
考虑三角形和四边形在形状上有什么性质不太一样,由于三角形是个等腰三角形,底边平行于水平面,高一定不小于2。因此三角形占据的行上的1的个数是不一样的。而矩形是一样的。
因此我们直接对每一行统计一下有多少1,如果有1就加入set。如果set最后的size()大于1,说明就是三角形,否则是正方形。
实际上我一开始根本就没看到等腰三角形底边平行于水平面的限制条件,不过不影响这么做。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#include <set>
using namespace std;int T,n;int main(){cin>>T;while(T--){cin>>n;set<int> S; for(int i=1;i<=n;i++){map<char,int> mp;string str;cin>>str;for(auto x:str)mp[x]++;if(mp['1'])S.insert(mp['1']);}if(S.size()>1)puts("TRIANGLE");else puts("SQUARE");}return 0;
}
C. Vlad and a Sum of Sum of Digits
题意:
请注意,本问题每次测试的时间限制仅为 0.5 秒。
弗拉迪斯拉夫在黑板上写下从 1 1 1 到 n n n 的整数。弗拉迪斯拉夫在黑板上写下了从 1 1 1 到 n n n 的整数,然后将每个整数替换为其数位之和。
现在黑板上的数字之和是多少?
例如,如果是 n = 12 n=12 n=12 ,那么最初黑板上的数字是 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 1,2,3,4,5,6,7,8,9,10,11,12,那么在替换之后,数字变成了 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 1 , 2 , 3 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3 1,2,3,4,5,6,7,8,9,1,2,3,这些数字之和为 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 1 + 2 + 3 = 51 1+2+3+4+5+6+7+8+9+1+2+3=51 1+2+3+4+5+6+7+8+9+1+2+3=51 。因此,对于 n = 12 n=12 n=12 ,答案是 51 51 51 。
思路:
发现数据范围并不大,所以我们可以直接暴力来算,不过由于 n ∗ t n*t n∗t 比较大,不能每次都暴力来算,所以考虑预处理+前缀和。之后直接查询即可。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=2e5+5;
typedef long long ll;int T,n;
ll a[maxn];ll f(int x){int tmp=0;while(x){tmp+=x%10;x/=10;}return tmp;
}int main(){for(int i=1;i<=2e5;i++)a[i]=a[i-1]+f(i);cin>>T;while(T--){cin>>n;cout<<a[n]<<endl;}return 0;
}
D. Vlad and Division
题意:
弗拉迪斯拉夫有 n n n 个非负整数,他想把所有这些数分成几组,这样在任何一组中,两数的二进制位从第 1 1 1 到 第 31 31 31 位都不相同。
形式化地来说,对于整数 k k k ,让 k 2 ( i ) k_2(i) k2(i) 表示其二进制表示中的第 i i i 位(从右到左,从1开始索引)。例如,如果是 k = 43 k=43 k=43 ,因为是 43 = 10101 1 2 43=101011_2 43=1010112 ,所以是 4 3 2 ( 1 ) = 1 43_2(1)=1 432(1)=1 、 4 3 2 ( 2 ) = 1 43_2(2)=1 432(2)=1 、 4 3 2 ( 3 ) = 0 43_2(3)=0 432(3)=0 、 4 3 2 ( 4 ) = 1 43_2(4)=1 432(4)=1 、 4 3 2 ( 5 ) = 0 43_2(5)=0 432(5)=0 、 4 3 2 ( 6 ) = 1 43_2(6)=1 432(6)=1 、 4 3 2 ( 7 ) = 0 43_2(7)=0 432(7)=0 、 4 3 2 ( 8 ) = 0 , … , 4 3 2 ( 31 ) = 0 43_2(8)=0, \dots, 43_2(31)=0 432(8)=0,…,432(31)=0 。
形式上,对于同一组中的任意两个数 x x x 和 y y y ,条件 x 2 ( i ) ≠ y 2 ( i ) x_2(i) \neq y_2(i) x2(i)=y2(i) 必须对所有的 1 ≤ i < 32 1 \leq i\lt32 1≤i<32 成立。
弗拉德至少需要多少组才能实现他的目标?每个数字必须正好属于一组。
思路:
我们任取两个数比较是否能对起来比较慢,但是我们直接用一个数来算它的另一半,然后去找有没有就很快。我们直接用 31 31 31 个 1 1 1 (2147483647)异或一个数就能找到它的另一半了。
所以我们把所有数放到map里,第二维存储个数,每次拿到一个数就找一下它的另一半,然后贪心地减掉能分的组数(两个数个数的最小值),记录进答案,最后在找一遍不能分组的单独加入答案即可。
code:
#include <iostream>
#include <cstdio>
#include <map>
using namespace std;int T,n;int main(){cin>>T;while(T--){cin>>n;map<int,int> mp;for(int i=1,t;i<=n;i++){cin>>t;mp[t]++;}int sz=0;for(auto &x:mp){int t=2147483647^x.first,m=min(x.second,mp[t]);x.second-=m;mp[t]-=m;sz+=m;}for(auto x:mp)sz+=x.second;cout<<sz<<endl;}return 0;
}
E. Vlad and an Odd Ordering
题意:
弗拉迪斯拉夫有编号为 1 , 2 , … , n 1, 2, \dots, n 1,2,…,n 的 n n n 张牌。他想把这些牌按如下方式排成一排:
- 首先,他把所有奇数牌从小到大依次铺开。
- 接着,他放下所有从小到大是奇数两倍的牌(即 2 2 2 乘以一个奇数)。
- 接着,他放下所有从小到大是奇数的 3 3 3 倍(即 3 3 3 乘以奇数)的牌。
- 接着,他放下所有从小到大 4 4 4 乘以一个奇数(即 4 4 4 乘以一个奇数)的牌。
- 依此类推,直到所有的牌都放下为止。
在这个过程中,他放下的第 k k k 张牌是什么?一旦弗拉迪斯拉夫放下一张牌,他就不能再用这张牌了。
思路:
好优美的数学题。
我们先把放下牌的序列写一下:
| 轮次 | 序列 |
|---|---|
| 第一轮 | 1 , 3 , 5 , 7 , 9 , 11 , 13 , 15 , 17 , 19 , 21 , … 1,3,5,7,9,11,13,15,17,19,21,\dots 1,3,5,7,9,11,13,15,17,19,21,… |
| 第二轮 | 2 , 6 , 10 , 14 , 18 , 22 , 26 , 30 , 34 , 38 , … 2,6,10,14,18,22,26,30,34,38,\dots 2,6,10,14,18,22,26,30,34,38,… |
| 第三轮 | 3 , 9 , 15 , 21 , … 3,9,15,21,\dots 3,9,15,21,… |
| 第四轮 | 4 , 12 , 20 , 28 , … 4,12,20,28,\dots 4,12,20,28,… |
| 第五轮 | 5 , 15 , 25 , 35 , … 5,15,25,35,\dots 5,15,25,35,… |
我们发现第二轮的牌和第一轮是不会重复的,因为第二轮的牌一定都是偶数。第三轮的牌一定和第一轮的牌重复,因为第三轮的牌都是奇数,而第一轮的牌包含所有计数。第四轮的牌我们无论怎么列,都不会和第一轮以及第二轮重复,这是为什么呢。
考虑描述以下每张牌,第一轮我们拿出的第 k k k 张牌是 2 k − 1 2k-1 2k−1,第二轮我们拿出的第 k k k 张牌是 2 ∗ ( 2 k − 1 ) 2*(2k-1) 2∗(2k−1),第三轮我们拿出的第 k k k 张牌是 3 ∗ ( 2 k − 1 ) 3*(2k-1) 3∗(2k−1)… 第 m m m 轮我们拿出的第 k k k 张牌是 m ∗ ( 2 k − 1 ) m*(2k-1) m∗(2k−1)。
如果要第二轮的牌和第一轮的牌重复,那么就有: 2 k 1 − 1 = 2 ∗ ( 2 k 2 − 1 ) 2k_1-1=2*(2k_2-1) 2k1−1=2∗(2k2−1),如果 k 1 , k 2 k_1,k_2 k1,k2 是整数,那么这个式子显然不可能成立,因为等式左边是奇数,而右边是偶数。
同理证明第四轮的牌和第一二轮的牌不重复,和第一轮的牌不重复是显然的,看第二轮,那么有: 2 ∗ ( 2 k 2 − 1 ) = 4 ∗ ( 2 k 4 − 1 ) 2*(2k_2-1)=4*(2k_4-1) 2∗(2k2−1)=4∗(2k4−1) ∴ 2 k 2 − 1 = 2 ∗ ( 2 k 4 − 1 ) \therefore2k_2-1=2*(2k_4-1) ∴2k2−1=2∗(2k4−1)咦?这好像就转化成了上面那种情况了。它们的系数相当于轮数,这意味着如果我们给第二轮的所有牌上的数都除以2,所得的情形其实就与第一轮的牌和第二轮的牌一致。不然你可以给第二轮和第四轮的牌都除以2,再与第一轮和第二轮的牌比较。
这个道理是可以向下继续推的,第一轮与第二轮不重复,第二轮与第四轮不重复,第四轮与第八轮不重复。而其他的轮数拿出来的牌都是重复的。
那么我们现在可以重新书写一下轮数,我们第 m m m 个有效的序列其实对应着原来的第 2 m − 1 2^{m-1} 2m−1 轮,这一轮的数列是 m ∗ ( 2 k − 1 ) m*(2k-1) m∗(2k−1)。所以我们直接假设第 m m m 轮的数列是 2 m ∗ ( 2 k − 1 ) 2^m*(2k-1) 2m∗(2k−1) ( m m m 从 0 0 0 开始)
现在知道了每一轮是啥,每个数是啥,要找第 x x x 大的数,显然的想法是算出每一轮有几个数,然后不断给 x x x 减去,直到减不了为止,答案就落到了这个序列中。
怎么算每一轮的个数?找出满足条件的最大值即可,即 2 m ∗ ( 2 k − 1 ) ≤ x 2^m*(2k-1)\le x 2m∗(2k−1)≤x算出最大的 k k k 就是个数。 2 m ∗ ( 2 k − 1 ) ≤ x 2^m*(2k-1)\le x 2m∗(2k−1)≤x 2 k − 1 ≤ x 2 m 2k-1\le \frac x{2^m} 2k−1≤2mx k ≤ x 2 m + 1 2 = x + 2 m 2 m + 1 k\le \frac {\frac x{2^m}+1}{2}=\frac { x+2^m}{2^{m+1}} k≤22mx+1=2m+1x+2m ∵ k 是整数 ∴ k = ⌊ x + 2 m 2 m + 1 ⌋ = ⌊ x 2 m + 1 + 1 2 ⌋ \because k是整数\therefore k=\left\lfloor\frac { x+2^m}{2^{m+1}}\right\rfloor=\left\lfloor\frac { x}{2^{m+1}}+\frac12\right\rfloor ∵k是整数∴k=⌊2m+1x+2m⌋=⌊2m+1x+21⌋
发现当 m m m 增大时, k k k会急剧减小,直到永远为 0 0 0,具体的来说,当 m > l o g 2 x m>log_2x m>log2x 时, k = 0 k=0 k=0,这时一定放下了所有牌(因为我们的游戏规则导致了我们一定可以放下所有牌)。所以我们的枚举其实只需要 l o g 2 x log_2x log2x 次就行了。总的时间复杂度是 O ( t ∗ l o g 2 k ) O(t*log_2k) O(t∗log2k),可以通过本题。
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;int T;
ll n,k;inline ll f(ll n,ll m){return (n+(1LL<<m))/(1LL<<(m+1));}int main(){cin>>T;while(T--){cin>>n>>k;ll m=0;while(k>f(n,m)){k-=f(n,m);m++;}cout<<(1LL<<m)*(2*k-1)<<endl;}return 0;
}
F. Vlad and Avoiding X
题意:
弗拉迪斯拉夫有一个大小为 7 × 7 7 \times 7 7×7 的网格,其中每个单元格的颜色都是黑色或白色。在一次操作中,他可以选择任何一个单元格并改变其颜色(黑色 ↔ \leftrightarrow ↔ 白色)。
求最少需要多少次操作才能确保没有黑色单元格的对角线上的四个相邻单元格也是黑色的。

左图显示,最初有两个黑色单元格违反了条件。只要翻转一个单元格,网格就能正常工作。
思路1(迭代加深搜索+剪枝):
尝试了各种各样的暴力姿势,不得不说这题真挺好。
发现数据范围是 7 × 7 7\times 7 7×7 的,事情必有蹊跷,尝试爆搜。不过裸爆搜肯定会T,尝试每个位置改为W,最坏情况下是 49 49 49 个位置都尝试改一遍,时间复杂度是 2 49 2^{49} 249 直接卡飞。
经过手玩,发现答案最多不会超过 8 8 8 ,也就是把中间那个 3 × 3 3\times3 3×3 的正方形的边上的 8 8 8 个点删掉就行了。考虑剪枝,我们加入这个限制条件之后,搜索树搜索到的所有终点状态其实相当于在图上随便选取 0 ∼ 8 0\sim8 0∼8 个B改成W点的选择数。这样的话总的搜索次数就是 ∑ i = 0 8 C 49 i \sum_{i=0}^{8}C_{49}^i ∑i=08C49i,还是会超时。
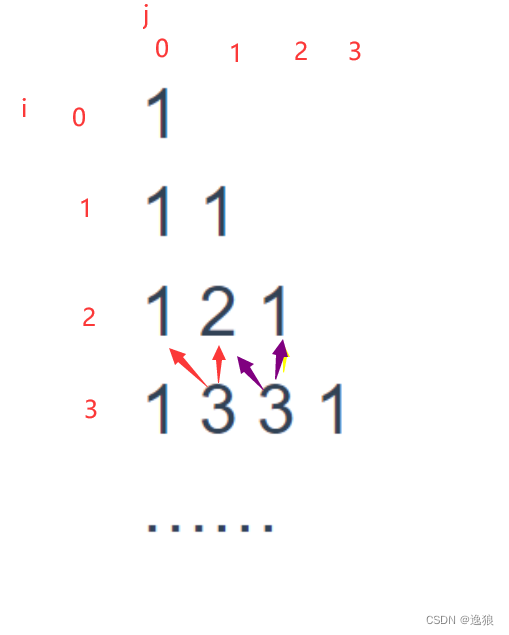
考虑继续剪枝,发现最外面一圈的点是肯定没必要选的,否则我们可以把它等效替换成外三环的点。举个例子,如下图,假如我们要选择红色点,说明我们要拆掉图上的两个紫色的叉型,那么我们可以直接替换成蓝色点即可,一定更优。其他的点同理。

通过这个思路,可以优化掉一半的点,终点状态有 ∑ i = 0 8 C 25 i = 1807781 \sum_{i=0}^{8}C_{25}^i=1807781 ∑i=08C25i=1807781 个。
发现八个点的状态没必要搜索,因为答案最差就是8,无法优化答案,所以找7个点即可,终点状态优化为 ∑ i = 0 7 C 25 i = 726206 \sum_{i=0}^{7}C_{25}^i=726206 ∑i=07C25i=726206 个,如果最坏情况跑满,跑 t = 200 t=200 t=200 次,跑的总次数差不多是 1.5 ∗ 1 0 8 1.5*10^8 1.5∗108,但是我们每次检查状态还需要至少 25 25 25 次查询, 1.5 ∗ 1 0 8 ∗ 25 1.5*10^8*25 1.5∗108∗25,这样很容易就寄了加点神秘优化应该能过。
发现瓶颈出现在每次转移到新状态都要查询当前状态是否合法,以及我们的搜索的到的答案顺序不是有序的,这意味着我们必须搜完所有可能的状态。
因为每次深度搜索增加1的时候,搜索树的规模就会剧增(比倍增还快),所以考虑迭代加深搜索,预先设定好搜索深度(也就是选几个点),如果深度到达预期才检查状态并返回,由于我们设定的深度是从小到大的,所以我们搜到的第一个合法的答案就是最小的答案。这样一次搜索的最坏要搜索 C 25 7 = 480700 C_{25}^7=480700 C257=480700 个终点状态,而检查的函数,一个一个枚举时由于碰到不合法的点就会提前返回,远远跑不满 25 25 25,所以实际时间复杂度远远跑不到 25 ∗ C 25 7 ≈ 1.2 ∗ 1 0 7 25*C_{25}^7\approx1.2*10^7 25∗C257≈1.2∗107,实际跑下来最坏情况(全都是B)(算上迭代加深所有的深度)检查枚举的次数其实只有 2164121 ≈ 2 ∗ 1 0 6 2164121\approx 2*10^6 2164121≈2∗106 次,跑满 t t t 次需要约 4 ∗ 1 0 9 4*10^9 4∗109 次,极限数据下最慢会跑 2 s 2s 2s 多一点,可以通过本题。如果深度变浅,搜索的规模会大幅降低,比如平均深度为7时搜索的时间为 1200 m s 1200ms 1200ms 左右,平均为6时为 900 m s 900ms 900ms 左右,平均为5时为 400 m s 400ms 400ms 左右。
code1:
迭代加深搜索+剪枝
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;int T;
string mp[10];pair<int,int> nxtn(pair<int,int> a){a.second++;if(a.second>6){a.first++;a.second=2;}return a;
}
bool check(){for(int i=2;i<=6;i++)for(int j=2;j<=6;j++)if(mp[i][j]=='B' && mp[i-1][j-1]=='B' && mp[i-1][j+1]=='B' && mp[i+1][j-1]=='B' && mp[i+1][j+1]=='B')return false;return true;
}
int ans;
bool dfs(int dep,int mxdep,pair<int,int> lst){if(dep==mxdep)return check();if(lst>make_pair(6,6))return false;pair<int,int> nw=nxtn(lst);if(mp[nw.first][nw.second]=='W')return dfs(dep,mxdep,nw);if(dfs(dep,mxdep,nw))return true;mp[nw.first][nw.second]='W';if(dfs(dep+1,mxdep,nw)){mp[nw.first][nw.second]='B';return true;}else {mp[nw.first][nw.second]='B';return false;}
}int main(){cin>>T;while(T--){ans=8;for(int i=1;i<=7;i++){cin>>mp[i];mp[i]=" "+mp[i];}for(int d=0;d<ans;d++)if(dfs(0,d,make_pair(2,1))){ans=d;break;}cout<<ans<<endl;}return 0;
}
对最坏情况进行打表输出,其他情况剪枝爆搜的“分治”做法(3000ms),相当神秘。
不过由于是对特殊情况打表,所以仍然可以被hack(被我亲手hack掉了)

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;int T;
string mp[10];pair<int,int> nxtn(pair<int,int> a){a.second++;if(a.second>6){a.first++;a.second=2;}return a;
}
bool check(){for(int i=2;i<=6;i++)for(int j=2;j<=6;j++){if(mp[i][j]=='B' && mp[i-1][j-1]=='B' && mp[i-1][j+1]=='B' && mp[i+1][j-1]=='B' && mp[i+1][j+1]=='B')return false;}return true;
}
int ans;
void dfs(int cnt,pair<int,int> lst){if(cnt>=ans)return;if(lst>make_pair(6,6))return;if(check()){ans=min(ans,cnt);return;}pair<int,int> nw=nxtn(lst);int x=nw.first,y=nw.second;if(mp[x][y]=='W')dfs(cnt,nw);else {dfs(cnt,nw);mp[x][y]='W';dfs(cnt+1,nw);mp[x][y]='B';}
}int main(){cin>>T;while(T--){for(int i=1;i<=7;i++){cin>>mp[i];mp[i]=" "+mp[i];}bool flag=false;//对全部为B的数据的特判for(int i=1;i<=7;i++)if(mp[i]!=" BBBBBBB"){flag=true;break;}if(!flag){cout<<8<<endl;continue;}ans=8;dfs(0,make_pair(2,1));cout<<ans<<endl;}return 0;
}
思路2(两次搜索):
假设我们用中心点的位置表示一个叉型的位置,我们发现所有的两个相邻的叉号它们的点完全不重合,中心点隔了偶数步的点才可能有交集,而隔了奇数步的叉号永远不可能产生交集。就好像是两个世界里的人。

对一个 7 ∗ 7 7*7 7∗7 的网格,红色点上的叉号和绿色点上的叉号两者互相不影响,所以我们可以分开来看红色点和绿色点。分别对红色点和绿色的位置进行爆搜换点,使得红色位置和绿色位置的叉号分别满足条件,答案数相加就是最后答案。
再根据我们上面的剪枝思路:最外边一圈的点不用换,总的搜索次数最坏最坏是 ( 2 13 ∗ 13 + 2 12 ∗ 12 ) ∗ t = 31129600 ≈ 3 ∗ 1 0 8 (2^{13}*13+2^{12}*12)*t=31129600\approx 3*10^8 (213∗13+212∗12)∗t=31129600≈3∗108 次,丢上去的瞬间就A了。。
code:
187ms…
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define pii pair<int,int>int T;
string mp[10];bool check(int x){for(int i=2;i<=6;i++)for(int j=2;j<=6;j++){if((i^j^x)&1)continue;if(mp[i][j]=='B' && mp[i-1][j-1]=='B' && mp[i-1][j+1]=='B' && mp[i+1][j-1]=='B' && mp[i+1][j+1]=='B')return false;}return true;
}
pii nxtn(pii a){a.second+=2;if(a.second>6){a.first++;a.second-=5;}return a;
}int ans;
void dfs(pii lst,int res){if(lst>pii(6,6)){if(check((lst.first+lst.second)&1))ans=min(ans,res);return;}pii nw=nxtn(lst);int x=nw.first,y=nw.second;if(mp[x][y]=='W')dfs(nw,res);else {dfs(nw,res);mp[x][y]='W';dfs(nw,res+1);mp[x][y]='B';}return;
}int main(){cin>>T;while(T--){for(int i=1;i<=7;i++){cin>>mp[i];mp[i]=" "+mp[i];}int x=0;ans=8;dfs(pii(2,0),0);x+=ans;ans=8;dfs(pii(2,1),0);x+=ans;cout<<x<<endl;}return 0;
}
G. Vlad and Trouble at MIT
题意:
弗拉迪斯拉夫有个儿子非常想去麻省理工学院。麻省理工学院(摩尔多瓦理工学院)的学生宿舍可以用一棵有 n n n 个顶点的树来表示,每个顶点代表一个房间,房间里正好有一个学生。树是一个连通的无向图,有 n n n 个顶点和 n − 1 n-1 n−1 条边。
今晚,有三种类型的学生:
- 想参加派对和玩音乐的学生(标记为 P \texttt{P} P )、
- 想睡觉和享受安静的学生(标记为 S \texttt{S} S ),以及
- 无所谓的学生(标记为 C \texttt{C} C )。
起初,所有的边缘都是薄墙,允许音乐通过,因此当参加派对的学生放音乐时,每个房间都能听到。但是,我们可以在任何边缘放置一些厚墙–厚墙不允许音乐通过。
学校希望安装一些厚墙,这样每个参加派对的学生都可以播放音乐,而睡觉的学生却听不到。
由于大学在冠名权诉讼中损失惨重,他们要求您找出他们需要使用的最少厚墙数量。
思路:
根据这个点有没有被音乐浸润,我们可以把每个点看作是三种类型之一——音趴点,睡觉点,无所谓点,分别用 0 , 1 , 2 0,1,2 0,1,2 来代替。可以发现,玩音乐的学生呆的点一定是音趴点,睡觉的学生呆的点一定是睡觉点,无所谓学生呆的点是什么无所谓。音趴点后面如果是音趴点和无所谓点就可以不在相连的边上加隔板,如果是睡觉点就要加一个隔板,同理睡觉点,而无所谓点就需要在音趴点和睡觉点之间加隔板。
这就相当于一个树上dp了。 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示把 j j j 号点看作 i i i 类型点, j j j 号点作为根时需要放的最少隔板数。如果一个儿子是 v i v_i vi ,那么从儿子推过来的递推方程为:
- 这个点 j j j 是音趴点:
d p [ 0 ] [ j ] = ∑ m a x { d p [ 0 ] [ v i ] , d p [ 1 ] [ v i ] + 1 , d p [ 3 ] [ v i ] } dp[0][j]=\sum max\{dp[0][v_i],dp[1][v_i]+1,dp[3][v_i]\} dp[0][j]=∑max{dp[0][vi],dp[1][vi]+1,dp[3][vi]}
d p [ 1 ] [ j ] = d p [ 2 ] [ j ] = ∞ dp[1][j]=dp[2][j]=\infty dp[1][j]=dp[2][j]=∞ - 这个点 j j j 是睡觉点:
d p [ 1 ] [ j ] = ∑ m a x { d p [ 0 ] [ v i ] + 1 , d p [ 1 ] [ v i ] , d p [ 3 ] [ v i ] } dp[1][j]=\sum max\{dp[0][v_i]+1,dp[1][v_i],dp[3][v_i]\} dp[1][j]=∑max{dp[0][vi]+1,dp[1][vi],dp[3][vi]}
d p [ 0 ] [ j ] = d p [ 2 ] [ j ] = ∞ dp[0][j]=dp[2][j]=\infty dp[0][j]=dp[2][j]=∞ - 这个点 j j j 是无所谓点:
d p [ 0 ] [ j ] = ∑ m a x { d p [ 0 ] [ v i ] , d p [ 1 ] [ v i ] + 1 , d p [ 3 ] [ v i ] } dp[0][j]=\sum max\{dp[0][v_i],dp[1][v_i]+1,dp[3][v_i]\} dp[0][j]=∑max{dp[0][vi],dp[1][vi]+1,dp[3][vi]}
d p [ 1 ] [ j ] = ∑ m a x { d p [ 0 ] [ v i ] + 1 , d p [ 1 ] [ v i ] , d p [ 3 ] [ v i ] } dp[1][j]=\sum max\{dp[0][v_i]+1,dp[1][v_i],dp[3][v_i]\} dp[1][j]=∑max{dp[0][vi]+1,dp[1][vi],dp[3][vi]}
d p [ 2 ] [ j ] = ∑ m a x { d p [ 0 ] [ v i ] + 1 , d p [ 1 ] [ v i ] + 1 , d p [ 3 ] [ v i ] } dp[2][j]=\sum max\{dp[0][v_i]+1,dp[1][v_i]+1,dp[3][v_i]\} dp[2][j]=∑max{dp[0][vi]+1,dp[1][vi]+1,dp[3][vi]}
dfs回溯的时候算一下dp值即可。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int maxn=1e5+5;
const int inf=1e8; int T,n;
vector<int> e[maxn];
void add(int u,int v){e[u].push_back(v);
}string st;
int dp[5][maxn];//节点类型 节点编号
void dfs(int u,int rt){if(st[u]=='P')dp[0][u]=0,dp[1][u]=dp[2][u]=inf;else if(st[u]=='S')dp[1][u]=0,dp[0][u]=dp[2][u]=inf;else dp[1][u]=dp[0][u]=dp[2][u]=0;for(auto v:e[u]){if(v==rt)continue;dfs(v,u);if(st[u]=='P'){//音趴点 dp[0][u]+=min(min(dp[0][v],dp[1][v]+1),dp[2][v]);}else if(st[u]=='S'){//睡大觉点 dp[1][u]+=min(min(dp[1][v],dp[0][v]+1),dp[2][v]);}else {//无所谓 dp[0][u]+=min(min(dp[0][v],dp[1][v]+1),dp[2][v]);dp[1][u]+=min(min(dp[1][v],dp[0][v]+1),dp[2][v]);dp[2][u]+=min(min(dp[0][v]+1,dp[1][v]+1),dp[2][v]);}}return;
}int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)e[i].clear();for(int u=2,v;u<=n;u++){cin>>v;add(u,v);add(v,u);}cin>>st;st=" "+st;dfs(1,-1);cout<<min(min(dp[0][1],dp[1][1]),dp[2][1])<<endl;;}return 0;
}
发现其实无所谓点是可以不存在的,如果树上有一段是无所谓段,那么我们可以把它合并到与它相邻的音趴段或者睡觉段上,而隔板数不变,所以dp可以少推一个状态。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int maxn=1e5+5;
const int inf=1e8; int T,n;
vector<int> e[maxn];
void add(int u,int v){e[u].push_back(v);
}string st;
int dp[5][maxn];//节点类型 节点编号
/*
音趴点的后继节点必须
*/
void dfs(int u,int rt){if(st[u]=='P')dp[0][u]=0,dp[1][u]=inf;else if(st[u]=='S')dp[1][u]=0,dp[0][u]=inf;else dp[1][u]=dp[0][u]=0;for(auto v:e[u]){if(v==rt)continue;dfs(v,u);if(st[u]=='P'){//音趴点 dp[0][u]+=min(dp[0][v],dp[1][v]+1);}else if(st[u]=='S'){//睡大觉点 dp[1][u]+=min(dp[1][v],dp[0][v]+1);}else {//无所谓 dp[0][u]+=min(dp[0][v],dp[1][v]+1);dp[1][u]+=min(dp[1][v],dp[0][v]+1);}}return;
}int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)e[i].clear();for(int u=2,v;u<=n;u++){cin>>v;add(u,v);add(v,u);}cin>>st;st=" "+st;dfs(1,-1);cout<<min(dp[0][1],dp[1][1])<<endl;;}return 0;
}