文章目录
- 2. 简单应力状态下的应力应变关系
- 2.1 简单拉伸的应力应变关系
- 2.2 真实应力应变关系
- 2.3 应力-应变关系简化模型
2. 简单应力状态下的应力应变关系
我们在高中就学过,弹簧拉伸力和变形量成比例,对于一般的金属材料,在一定载荷以内这种结论也是成立的,这种情况称之为弹性。在下面的材料力学单向拉伸试验的结果中,我们可以看到材料先发生弹性变形,超过一定极限后产生塑性变形。
2.1 简单拉伸的应力应变关系
材料拉伸试样如下图1所示,在试验时在试样两端夹持,施加载荷,试验在载荷作用下会伸长,记录相应时刻的载荷-位移数据,并以此绘制曲线如下图2所示。

图 1 拉伸试样 图1 \quad拉伸试样 图1拉伸试样
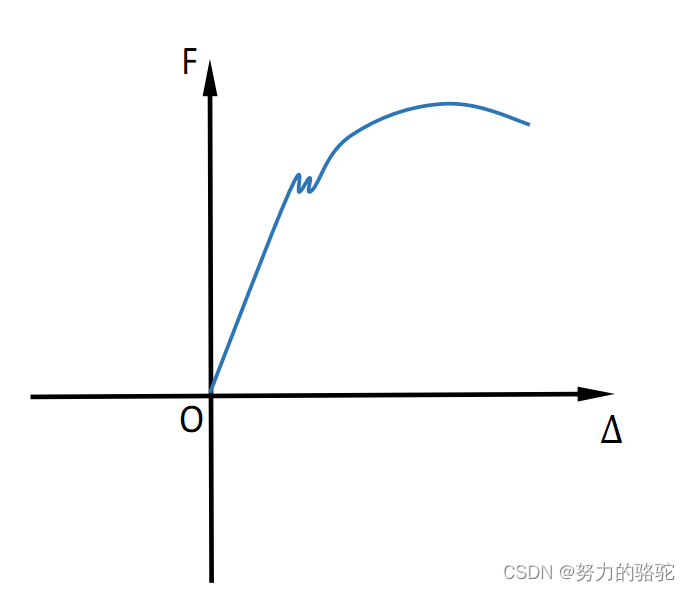
图 2 载荷 − 变形曲线 图2 \quad载荷-变形曲线 图2载荷−变形曲线
但一般会进行以下变换
σ = F A 0 , ε = Δ l 0 (1) \sigma=\frac{F}{A_0}, \varepsilon=\frac{\Delta}{l_0}\tag{1} σ=A0F,ε=l0Δ(1)
那么可以将载荷-变形曲线变换成 σ − ε \sigma-\varepsilon σ−ε应力应变曲线,如下图3。
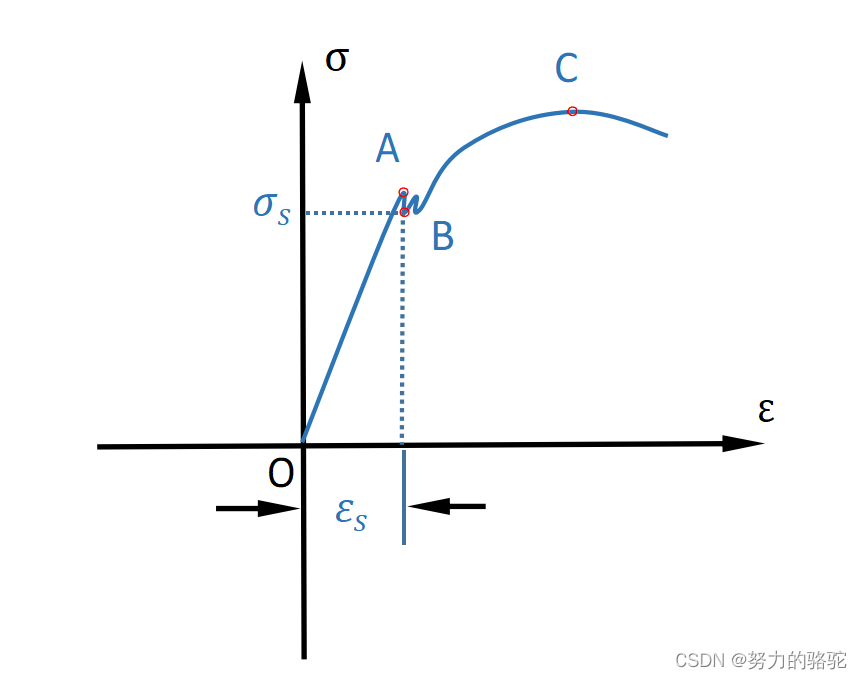
图 3 σ − ε 曲线 图3\quad \sigma-\varepsilon曲线 图3σ−ε曲线
其中A点称为上屈服点,B为下屈服点,材料在两者之间呈现流动状态,应力不发生显著变化只增加应变,一般上屈服点和下屈服点区别不大(此屈服流动的现象一般在低碳钢中存在,合金钢等往往没有明显的特征),用 σ s \sigma_s σs来代替,称材料的屈服强度。材料在 σ s \sigma_s σs以下呈现弹性变形,也就是载荷去除之后变形能够完全恢复,且应力和应变成比例。同时,金属材料压缩的应力应变曲线基本上与拉伸的应力应变曲线接近。
有一些金属可能没有上下屈服流动阶段,如下图4。
在应力超过弹性极限后,会产生塑性应变 ε p \varepsilon^p εp,缓慢卸去载荷,变形也不能完全恢复(见图4中 ε p \varepsilon^p εp),这种现象成为屈服。同时卸载曲线也是线性的,并且斜率和刚开始的弹性段一样,直到反向屈服。
图4中A’为材料的压缩屈服点,假设A与A’对称(即压缩屈服等于拉伸屈服),左图为多晶材料,多晶材料反向屈服点M’一般绝对值小于A’,称为包晶格效应(Bauschingerx effect),即在拉伸方向的强化导致压缩方向的弱化,这种效应在后文中还会应用(就是随动强化模型)。
右图为单晶材料,材料反向屈服点M’一般绝对值大于A’,即在拉伸方向的强化导致压缩方向的同样的强化,这种效应在后文中还会应用(就是等向强化模型)。

图 4 加载 / 卸载应力应变曲线 图4\quad 加载/卸载应力应变曲线 图4加载/卸载应力应变曲线
2.2 真实应力应变关系
在图3中,在应力达到最高点C以前,应力和应变一同增加,到达C点后应变增加,应力却下降了。事实上,在C点前由于泊松比的存在,变形前试样的截面随着载荷增加,会慢慢减小,但是在随着变形的继续,某一时刻横截面会较迅速的减小,这种现象称为颈缩(也称塑性失稳),由于截面的迅速缩小,试样的承载能力随之下降,相应的名义应力也下降。因此实际上,名义应力在变形量小的时候跟试样的真实应力差别不大,但是在颈缩时,名义应力和真实应力较大差别。
按照定义,定义真实应力 σ ~ \widetilde{\sigma} σ 如下
σ ~ = P A (2) \widetilde{\sigma}=\frac{P}{A}\tag{2} σ =AP(2)
其中 A A A为试样瞬时截面, P P P为试样瞬时载荷。
瞬时的应变增量 d ε ~ d\widetilde{\varepsilon} dε 如下所示
d ε ~ = d l ′ l ′ (3) d\widetilde{\varepsilon}=\frac{dl'}{l'}\tag{3} dε =l′dl′(3)
其中 l ′ l' l′为试样瞬时长度, d l ′ dl' dl′为试样瞬时伸长量。
那么真实应变 ε ~ \widetilde{\varepsilon} ε 为
ε ~ = ∫ l 0 l d l ′ l ′ = ln ( l ′ ) ∣ l 0 l = ln ( l l 0 ) = ln ( l − l 0 + l 0 l 0 ) = ln ( 1 + ε ) (4) \widetilde{\varepsilon}=\int_{l_0}^{l}\frac{dl'}{l'}=\ln(l')|_{l_0}^{l}=\ln(\frac{l}{l_0})=\ln(\frac{l-l_0+l_0}{l_0})=\ln(1+\varepsilon)\tag{4} ε =∫l0ll′dl′=ln(l′)∣l0l=ln(l0l)=ln(l0l−l0+l0)=ln(1+ε)(4)
在材料进入塑性阶段,材料表现出塑性流动的特征,这里需要引用材料几乎不可压缩的假设,因此有
A 0 l 0 = A l (5) A_0l_0=Al\tag{5} A0l0=Al(5)
那么真实应力变 σ ~ \widetilde{\sigma} σ 为
σ ~ = P A = P A 0 ⋅ A 0 A = P A 0 ⋅ l l 0 = σ e ε ~ = σ ( 1 + ε ) (6) \widetilde{\sigma}=\frac{P}{A}=\frac{P}{A_0}\cdot\frac{A_0}{A}=\frac{P}{A_0}\cdot\frac{l}{l_0}=\sigma e^{\widetilde{\varepsilon}}=\sigma (1+\varepsilon)\tag{6} σ =AP=A0P⋅AA0=A0P⋅l0l=σeε =σ(1+ε)(6)
在图5右侧曲线中C为名义应力达到最大值,在此时,有
d σ d ε = 0 (7) \frac{d\sigma}{d\varepsilon}=0\tag{7} dεdσ=0(7)
在图5右侧曲线中C为名义应力达到最大值对应的真实应力点C’’,其中真实应力有式(6),那么有
d σ ~ d ε = σ (8) \frac{d\widetilde{\sigma}}{d\varepsilon}=\sigma\tag{8} dεdσ =σ(8)
在图5左侧曲线中C为名义应力达到最大值对应的真实应力点C’,真实应力和真实应变应满足的条件如下
d σ ~ d ε ~ = ( d σ d ε ⋅ d ε d ε ~ ) e ε ~ + σ e ε ~ = σ e ε ~ = σ ~ (9) \frac{d\widetilde{\sigma}}{d\widetilde{\varepsilon}}=(\frac{d\sigma}{d\varepsilon}\cdot\frac{d\varepsilon}{d\widetilde{\varepsilon}})e^{\widetilde{\varepsilon}}+\sigma e^{\widetilde{\varepsilon}}=\sigma e^{\widetilde{\varepsilon}}=\widetilde{\sigma}\tag{9} dε dσ =(dεdσ⋅dε dε)eε +σeε =σeε =σ (9)
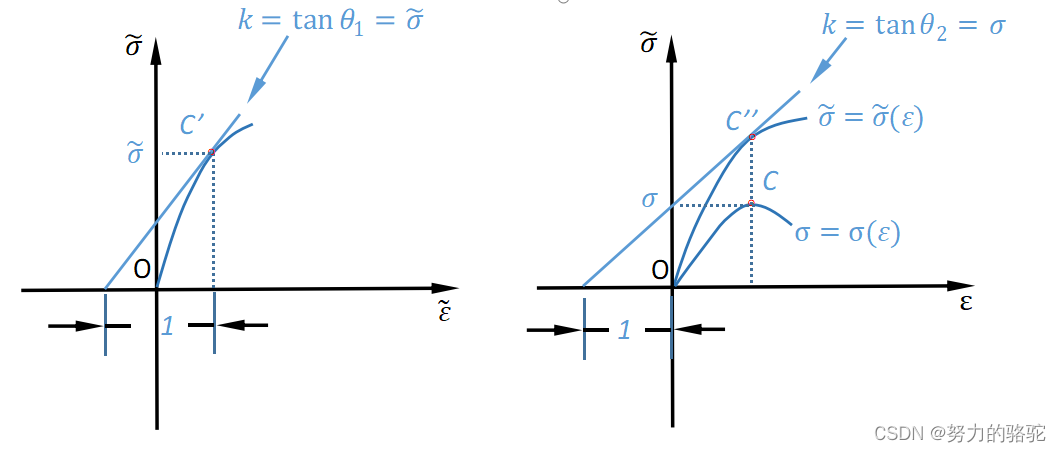
图 5 应力应变曲线 图5\quad 应力应变曲线 图5应力应变曲线
2.3 应力-应变关系简化模型
在理论分析中,常常采用简化的应力应变模型来分析具体问题(实际工程中也多有应用)。
简化模型一:理想弹塑性模型
如下图6所示,那么应力应变关系可以写为
σ = { E ε , ε ≤ ε s σ s s i g n ε , ε > ε s (10) \sigma=\begin{cases}E\varepsilon &\quad,\quad \varepsilon\le\varepsilon_s\\ \sigma_s sign \varepsilon &\quad,\quad \varepsilon\gt\varepsilon_s \end{cases}\tag{10} σ={Eεσssignε,ε≤εs,ε>εs(10)
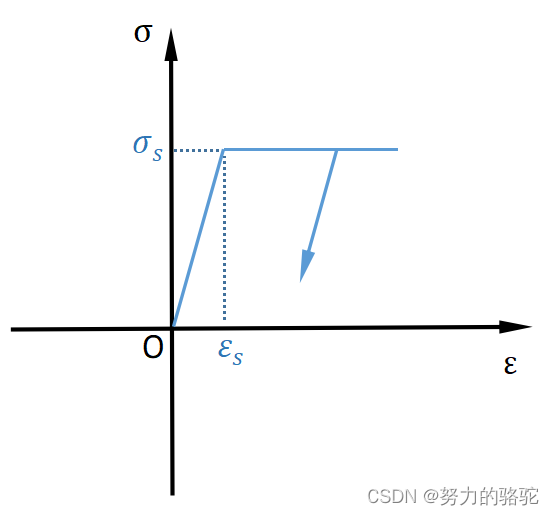
图 6 理想弹塑性模型 图6\quad 理想弹塑性模型 图6理想弹塑性模型
简化模型二:线性强化弹塑性模型
如下图7所示,那么应力应变关系可以写为
σ = { E ε , ε ≤ ε s σ s + E ’ ( ε − ε s ) , ε > ε s (11) \sigma=\begin{cases}E\varepsilon &\quad,\quad \varepsilon\le\varepsilon_s\\ \sigma_s +E’( \varepsilon-\varepsilon_s) &\quad,\quad \varepsilon\gt\varepsilon_s \end{cases}\tag{11} σ={Eεσs+E’(ε−εs),ε≤εs,ε>εs(11)
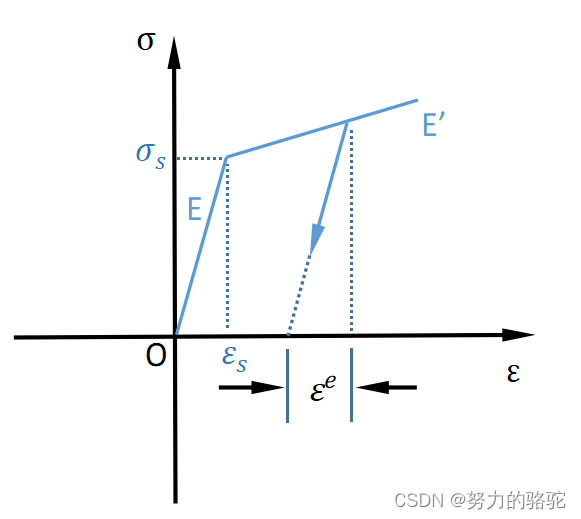
图 7 线性强化弹塑性模型 图7\quad 线性强化弹塑性模型 图7线性强化弹塑性模型
当然,上式当进入塑性后,还可以写成另外一种形式,如下所示
ε = ε e + ε p (12) \varepsilon=\varepsilon^e+\varepsilon^p\tag{12} ε=εe+εp(12)
σ = σ s + h ε p (13) \sigma=\sigma_s+h\varepsilon^p\tag{13} σ=σs+hεp(13)
可以通过下图来确定h,下图为应力-塑性应变图,由图7可知
E ′ = d σ d ε (14) E'=\frac{d\sigma}{d\varepsilon}\tag{14} E′=dεdσ(14)
同时由图8可知
h = d σ d ε p = d σ d ε − d ε e = 1 d ε d σ − d ε e d σ = 1 1 E ′ − 1 E (15) h=\frac{d\sigma}{d\varepsilon^p}=\frac{d\sigma}{d\varepsilon-d\varepsilon^e}=\frac{1}{\frac{d\varepsilon}{d\sigma}-\frac{d\varepsilon^e}{d\sigma}}=\frac{1}{\frac{1}{E'}-\frac{1}{E}}\tag{15} h=dεpdσ=dε−dεedσ=dσdε−dσdεe1=E′1−E11(15)
代入(13),那么有
ε p = σ − σ s h = ( σ − σ s ) ( 1 E ′ − 1 E ) \varepsilon^p=\frac{\sigma-\sigma_s}{h}=(\sigma-\sigma_s)(\frac{1}{E'}-\frac{1}{E}) εp=hσ−σs=(σ−σs)(E′1−E1)
那么相应的式(11)可以改写为
ε = ε e + ε p = σ E + ( σ − σ s ) ( 1 E ′ − 1 E ) (16) \varepsilon=\varepsilon^e+\varepsilon^p=\frac{\sigma}{E} +( \sigma-\sigma_s)(\frac{1}{E'}-\frac{1}{E})\tag{16} ε=εe+εp=Eσ+(σ−σs)(E′1−E1)(16)
同时,有
0 < 1 h = 1 E ′ − 1 E < 1 E ′ (17) 0\lt\frac{1}{h}=\frac{1}{E'}-\frac{1}{E}\lt\frac{1}{E'}\tag{17} 0<h1=E′1−E1<E′1(17)
那么有以下结论,
h > E ′ (18) h\gt E'\tag{18} h>E′(18)
而其物理意义如下图
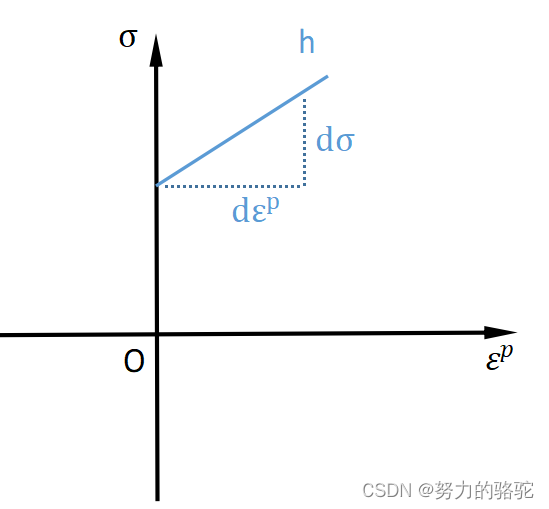
图 8 h 的物理意义(在 σ − ε p 图中) 图8\quad h的物理意义(在\sigma-\varepsilon^p 图中) 图8h的物理意义(在σ−εp图中)


![[OpenAI]继ChatGPT后发布的Sora模型解析与体验通道](https://img-blog.csdnimg.cn/direct/6f21b60b46e84e9aaec5932e802046ae.jpeg)
