Day 20
一、思路
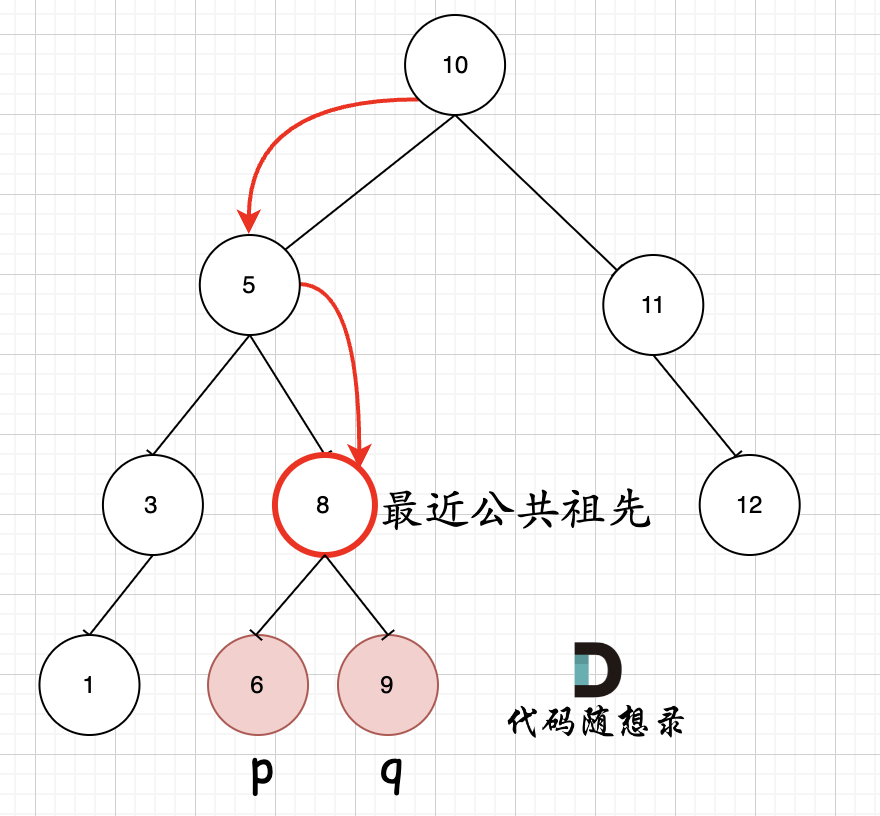
235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode)
秒,跟普通二叉树的区别在于
因为是有序树,所有 如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 一定是在 [p, q]区间的。
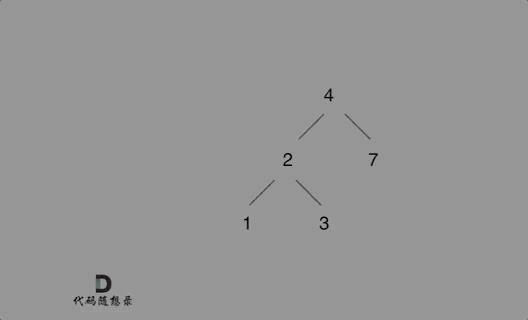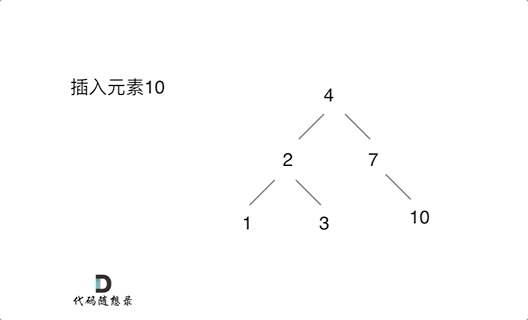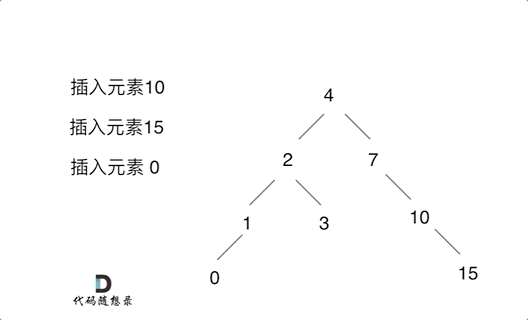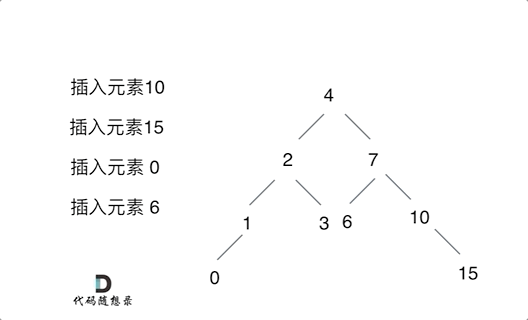
701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
也就是我们做题的时候 所谓的左旋和右旋
有以下五种情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
二、代码
235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==NULL) return root;if(p->val<=root->val && q->val>=root->val) return root;if(p->val>=root->val && q->val<=root->val) return root;TreeNode* left=lowestCommonAncestor(root->left,p,q);TreeNode* right=lowestCommonAncestor(root->right,p,q);if(left&&right) return root;else if(left && !right) return left;else return right;}
};
701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
嘻嘻嘻 一下就写出来了 嘻嘻嘻 开心
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if(root==nullptr){TreeNode* temp=new TreeNode(val);root=temp;return temp;}if(val<root->val &&root->left==nullptr){TreeNode* temp=new TreeNode(val);root->left=temp;return root;}if(val<root->val && root->left!=nullptr){insertIntoBST(root->left,val);}if(val>root->val &&root->right==nullptr){TreeNode* temp=new TreeNode(val);root->right=temp;return root;}if(val>root->val && root->right!=nullptr){insertIntoBST(root->right,val);}return root;}
};
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {//空if(root==nullptr) return root;if (root->val == key) {//叶子节点if(root->left==nullptr &&root->right==nullptr){delete root;return nullptr;}//单亲(一)else if(root->left==nullptr){// root->val=root->right->val;// delete root->right;// return root;auto retNode = root->right;///! 内存释放delete root;return retNode;}//单亲(二)else if(root->right==nullptr){// root->val=root->left->val;// delete root->left;// return root;auto retNode = root->left;///! 内存释放delete root;return retNode;}//健全else{TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置TreeNode* tmp = root; // 把root节点保存一下,下面来删除root = root->right; // 返回旧root的右孩子作为新rootdelete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};