本专栏内容为:算法学习专栏,分为优选算法专栏,贪心算法专栏,动态规划专栏以及递归,搜索与回溯算法专栏四部分。 通过本专栏的深入学习,你可以了解并掌握算法。
💓博主csdn个人主页:小小unicorn
⏩专栏分类:动态规划专栏
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
专题二
- 题目来源
- 题目描述
- 算法原理
- 1.状态表示
- 2.状态转移方程
- 3.初始化
- 4.填表顺序
- 5.返回值
- 代码实现
题目来源
本题来源为:
Leetcode 174. 地下城游戏
题目描述
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。

算法原理
1.状态表示
经验+题目要求

对于本题而言就是:
dp[i][j]表示:从[i,j]位置的出发,到达终点,所需要的最低初始健康点数
2.状态转移方程
分两种情况:
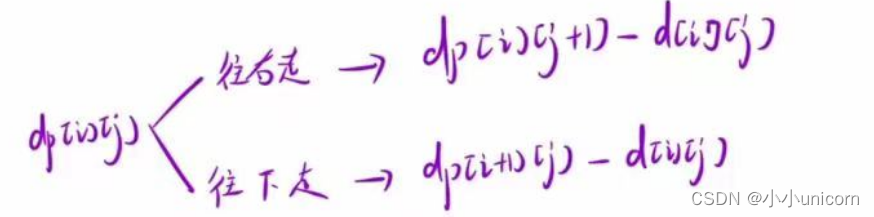
因此状态方程为:

为什么最后还要和1取Max呢?这是为了防止最后结果是个负数
dp[i][j]=min(dp[i+1][j],dp[i][j+1])-d[i][j];
dp[i][j]=max(1,dp[i][j]);
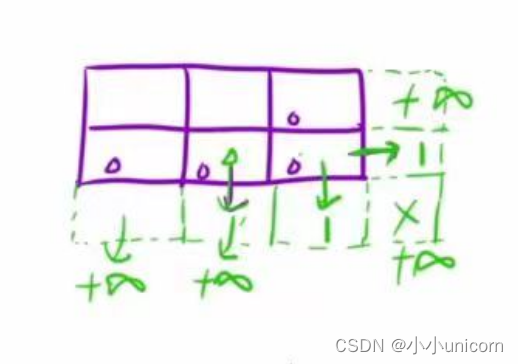
3.初始化
看图分析很容易就知道应该如何初始化。
4.填表顺序
从下往上填每一行,每一行从右往左
5.返回值
dp[0][0]
代码实现
动态规划的代码基本就是固定的四步:
1.创建dp表
2.初始化
3.填表
4.返回值
本题完整代码实现:
class Solution
{
public:int calculateMinimumHP(vector<vector<int>>& d) {int m=d.size(),n=d[0].size();//创建dp表vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));//初始化dp[m][n-1]=dp[m-1][n]=1;//填表for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){//状态转移方程dp[i][j]=min(dp[i+1][j],dp[i][j+1])-d[i][j];dp[i][j]=max(1,dp[i][j]);}}return dp[0][0];}
};
时间复杂度:O(MxN)
空间复杂度:O(MxN)