这是树的第11篇算法,力扣链接。
给你二叉树的根节点
root,返回它节点值的 前序 遍历。示例 1:
输入:root = [1,null,2,3] 输出:[1,2,3]
做了这么久的树问题,现在开始回忆三种遍历方法,这篇文章回忆的是前序遍历。
前序遍历 (Preorder Traversal)
在前序遍历中,节点的访问顺序如下:
- 访问根节点
- 遍历左子树
- 遍历右子树
前序遍历通常用于创建树的副本。当你访问节点之后立即复制节点,你可以通过前序遍历复制所有节点并创建一棵相同的树。
例子
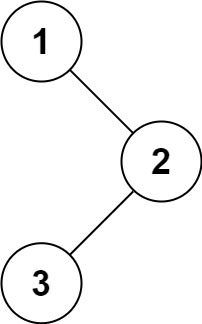
假设有一棵二叉树如下:
A/ \B C/ \ \ D E F对这棵树进行不同的遍历会得到以下结果:
- 前序遍历:
A, B, D, E, C, F。首先访问根节点(A),然后是左子树(B, D, E),最后是右子树(C, F)。
这里用迭代和递归一起回忆一下这个前序遍历的实现方法。
迭代思路是尽量选取左节点,当左节点没有的时候栈弹出选取右节点。
func preorderTraversal(root *TreeNode) []int {var result []intif root == nil {return result}stack := []*TreeNode{root}node := rootfor len(stack) > 0 {for node != nil {result = append(result, node.Val)stack = append(stack, node)node = node.Left}node = stack[len(stack)-1].Rightstack = stack[:len(stack)-1]}return result
}这是另一种写法,先把按照最左路径把右、左节点依次入栈。
func preorderTraversal(root *TreeNode) []int {var result []intif root == nil {return result}stack := []*TreeNode{root}node := rootfor len(stack) > 0 {node = stack[len(stack)-1]stack = stack[:len(stack)-1]result = append(result, node.Val)if node.Right != nil {stack = append(stack, node.Right)}if node.Left != nil {stack = append(stack, node.Left)}}return result
}
递归写法如下:
func preorderTraversal(root *TreeNode) []int {var result []intpreorder(root, &result)return result
}func preorder(node *TreeNode, result *[]int) {if node == nil {return}*result = append(*result, node.Val)preorder(node.Left, result)preorder(node.Right, result)
}还有指针的方法做的:
func PreorderTraversal(root *TreeNode) []int {var result []intcurrent := rootfor current != nil {if current.Left == nil {result = append(result, current.Val) // 访问当前节点current = current.Right // 移动到右子树} else {// 寻找前驱节点predecessor := current.Leftfor predecessor.Right != nil && predecessor.Right != current {predecessor = predecessor.Right}if predecessor.Right == nil {result = append(result, current.Val) // 访问当前节点// 将当前节点的右指针指向当前节点,建立一条回溯线索predecessor.Right = currentcurrent = current.Left // 移动到左子树} else {// 左子树已经访问完毕,恢复树的结构predecessor.Right = nilcurrent = current.Right // 移动到右子树}}}return result
}