day39打卡

62. 不同路径

状态表示

我们暂时设dp[i] [j]：以(i, j)为终点，所到达i使用的方法的数量

状态转移方程

从题目中可以看出，dp(i, j)的值取决于dp(i-1, j)和dp(i, j-1)的值，因为机器人只能向右或者向下走。

且我们猜测的状态表达式正好是到达以(i, j)为终点的方法。

dp[i][j] = dp[i-1][j] + dp[i][j-1]

初始化和填表

• 初始化

我们在初始化时，发现第一排和第一列都是相同的特殊情况，需要处理。

这很麻烦，所以我们多开辟一列和一排。

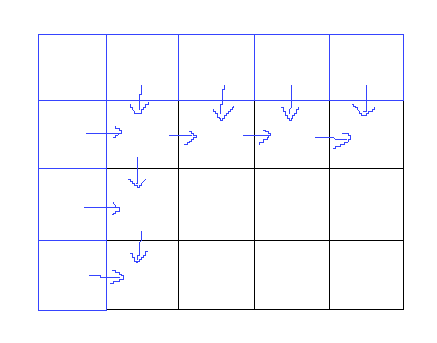
每一个格子都取决于前一个与上一个相加。

所以我们只需要初始化dp[0] [1] 或者 dp[1] [0] 为1即可。

• 填表

先填第一列，然后第二列，然后…

返回值

我们扩大了一列和一排，所以返回dp[m] [n]

class Solution {
public:int uniquePaths(int m, int n) {//创建dp数组vector<vector<int>> dp(m+1, vector<int>(n+1));//初始化dp[1][0] = 1;//填表for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}//返回值return dp[m][n];}
};

63. 不同路径 II

状态表示

dp[i] [j] ：以（i，j）为终点，到达（i，j）的方法的数量

状态转移方程

和上道题一样，取决于到达dp[i-1] [j] 和 dp[i] [j-1]的方法数量。

本题多了个障碍物，所以在填表时，判断一下对应位置是否有障碍物即可。有就不填写，没有就进行填写。

dp[i] [j] = dp[i-1] [j] + dp[i] [j-1]

初始化和填表

• 初始化

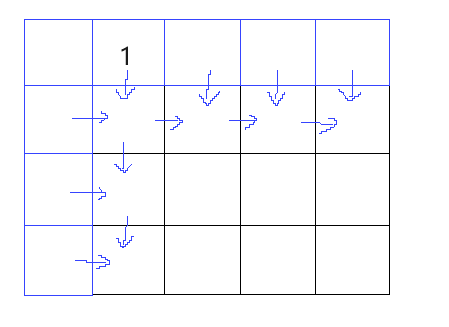
每一个格子都取决于前一个与上一个相加。

所以我们只需要初始化dp[0] [1] 或者 dp[1] [0] 为1即可。

• 填表

先填第一列，然后第二列，然后…

返回值

返回dp[m] [n]即可。

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {//创建dp数组int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1));//初始化dp[0][1] = 1;//填表for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(obstacleGrid[i-1][j-1] == 0)dp[i][j] = dp[i-1][j] + dp[i][j-1];}}//返回值return dp[m][n];}
};

dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
//返回值
return dp[m][n];
}
};