1.
![]()

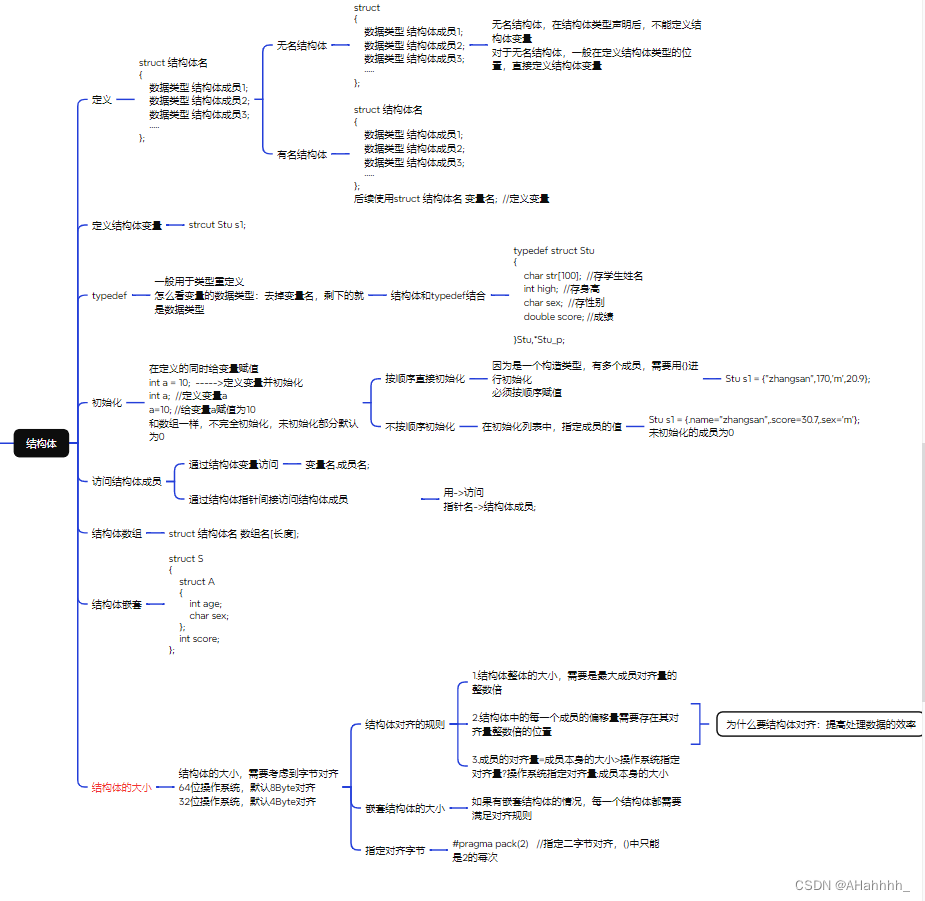
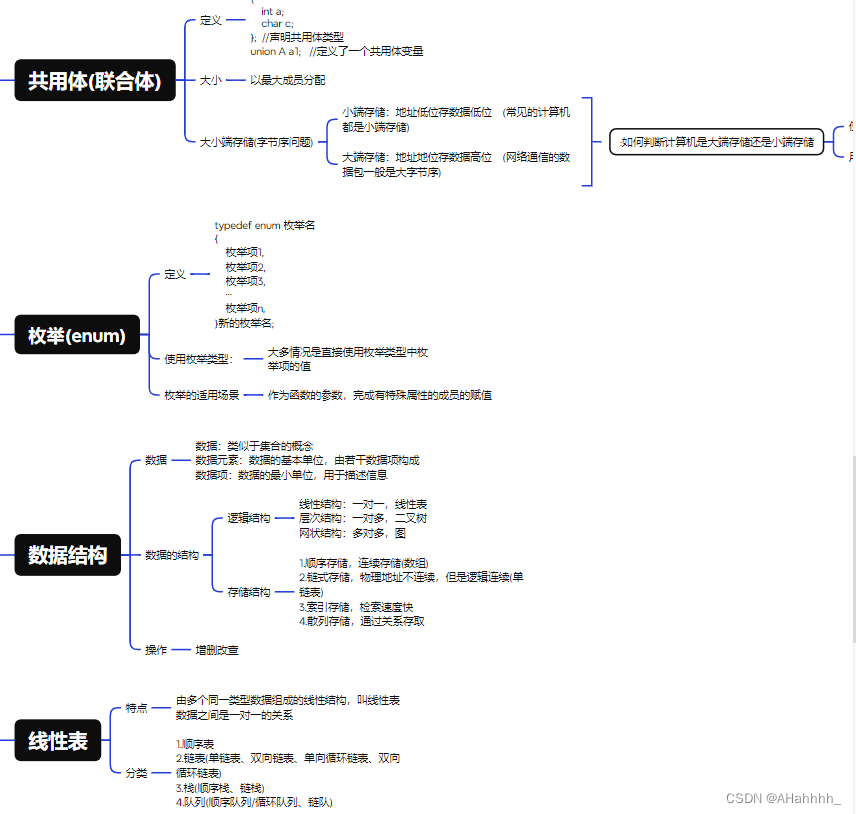
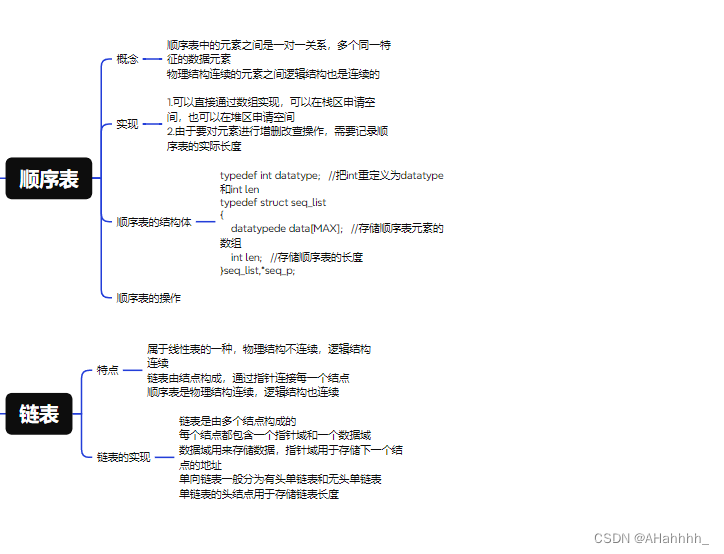
2.

按位插入
void insert_pos(seq_p L,datatype num,int pos)
{
if(L==NULL)
{
printf("入参为空,请检查\n");
return;
}
if(seq_full(L)==1)
{
printf("表已满,不能插入\n");
return;
}
if(pos==0)
{
insert_head(L,num);
return;
}
if(pos>=L->len)
{
printf("无法插入:位置不合理\n");
return;
}
if(pos==L->len)
{
insert_tail(L,num);
return;
}
for(int i=L->len-1;i>=pos;i--)
{
L->data[i+1]=L->data[i];
}
L->data[pos]=num;
L->len++;
}
按位删除
void del_pos(seq_p L,int pos)
{
if(L==NULL)
{
printf("入参为空\n");
return;
}
if(pos>=L->len)
{
printf("位置不合理\n");
return;
}
if(pos==0)
{
del_head(L);
return;
}
if(pos==L->len-1)
{
del_tail(L);
return;
}
for(int i=pos;i<=L->len-1;i++)
{
L->data[i]=L->data[i+1];
}
L->len--;
}
去重
void del_rep(seq_p L)
{
if(L==NULL)
{
printf("入参为空\n");
return;
}
for(int i=0;i<L->len;i++)
{
for(int j=i+1;j<L->len;j++)
{
if(L->data[i]==L->data[j])
{
del_pos(L,j);
j--;
}
}
}
}
3.

link.c
voidlink.c insert_head(link_p H,datatype data)
{
if(H==NULL)
{
printf("入参为空\n");
return;
}
link_p new=create_node(data);
new->next=H->next;
H->next=new;
H->len++;
}
尾插:
void insert_tail(link_p H,datatype data)
{
link_p temp=H;
for(int i=0;i<H->len;i++)
{
temp=temp->next;
}
link_p new=create_node(data);
temp->next=new;
new->next=NULL;
H->len++;
}
输出
void put_link(link_p H)
{
link_p temp=H;
for(int i=0;i<H->len;i++)
{
temp=temp->next;
printf("%d\t",temp->data);
}
printf("\n");
}
main.c
#include "link.h"
int main()
{
link_p H=create_head();
insert_head(H,2);
insert_head(H,1);
insert_tail(H,3);
put_link(H);
return 0;
}