B题 :智乃的数字手串

思路:
思维题,本题题意N个数组首尾相连,然后当某两个相邻数组和为偶数时,交替拿走,并在选择两个数字交换位置,直到没有可以操作的数字为止。
我们可以考虑,数字具有奇偶性,那么数字之和,同则偶,异则奇,那么当数组个数为奇数时一定是可以操作的,比如偶偶奇,奇偶偶,这种,一定是可以操作一次,而偶数是不一定可以操作的,所以玩家输掉游戏的时候,数组的个数一定是偶数,同时,拿走操作是交替进行的,所以第一次操作的时候数组个数是奇数,那么他进行操作的时候,数组个数就会一直是奇数,所以我们只需要看谁是第一个拿偶数的,谁就输掉游戏。
代码:
#include <iostream>
using namespace std;
int main()
{int t;cin>>t;while (t--){int n;cin>>n;for(int i=0;i<n;i++){int x;cin>>x;}if(n%2!=0) puts("qcjj");else puts("zn");}return 0;
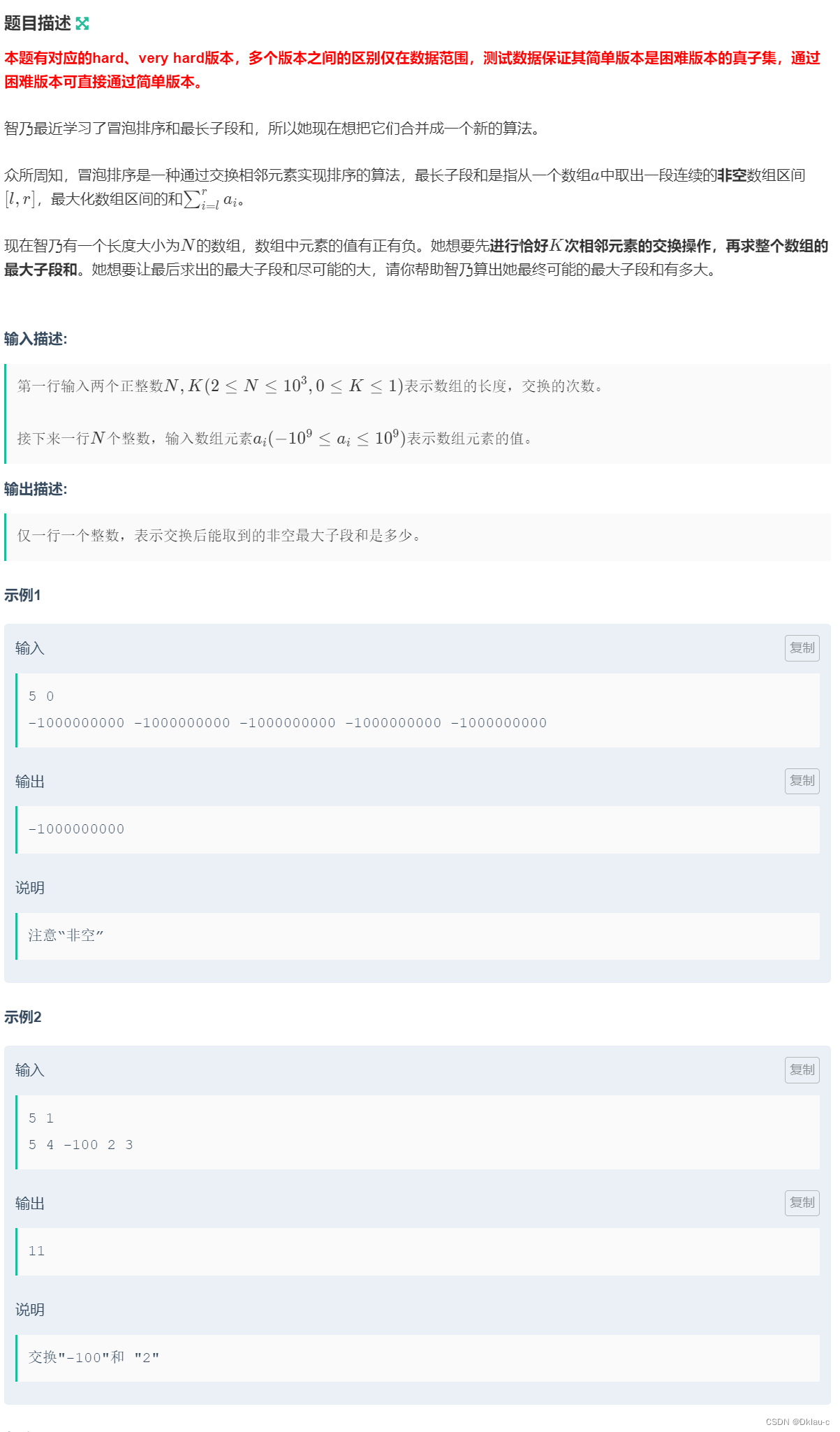
}D题:chino's bubble sort and maximum subarray sum(easy version)
思路:
因为本题N最大是10的3次方,而k最大是1,也就意味着,本题最多只会交换一次,所以根据k的值 遍历求最大子段和即可,
代码:
#include<iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=1e3+10;
int e[N];
int n,k;
long long ans=-1e18;
void solve()
{long long sum=0;for(int i=0;i<n;i++){sum+=e[i];if(sum<e[i]) sum=e[i]; //有可能 sum小于e[i],这个时候最大子段和是e[i]本身ans=max(ans,sum);}
}int main()
{cin>>n>>k;for(int i=0;i<n;i++){cin>>e[i];}if(k==0) solve();else {for(int i=0;i<n-1;i++){swap(e[i],e[i+1]);solve();swap(e[i],e[i+1]);}}cout<<ans<<endl;return 0;
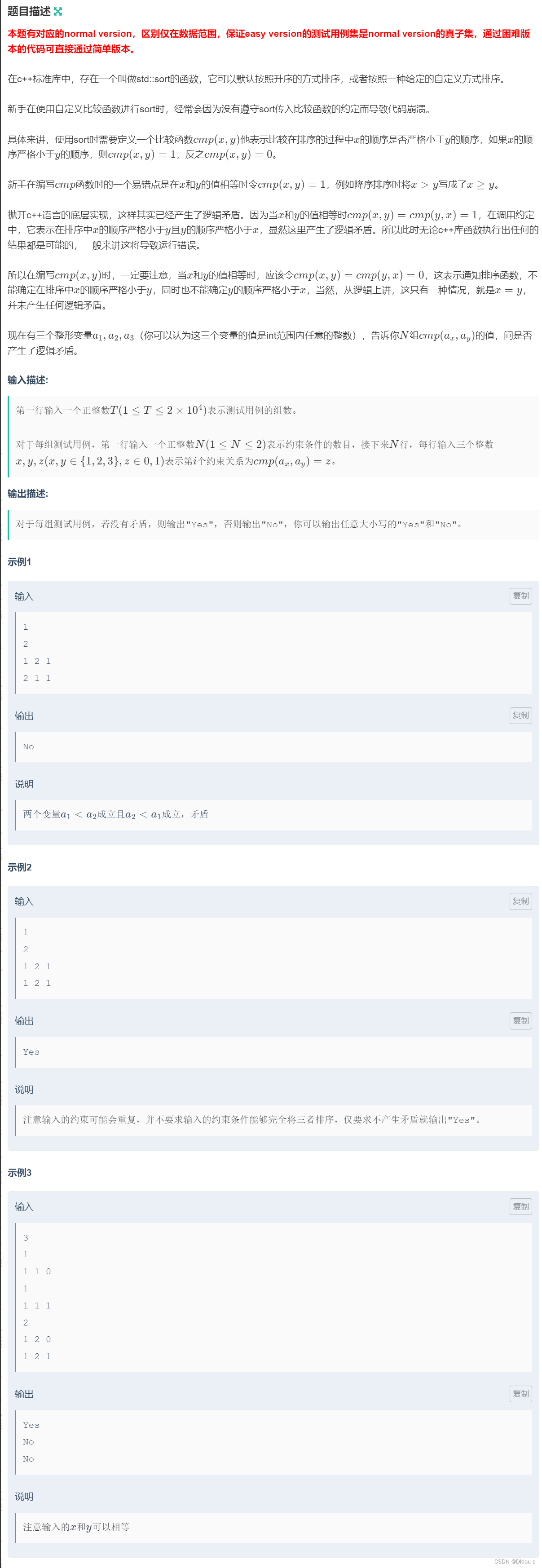
}G题:智乃的比较函数(easy version)
 思路1:
思路1:
本题N范围最大是2, 然后输入的整数也是在[1,3]范围内取整数,z也只取0和1,t最大是2*10的4次方,所以本题可以用暴力遍历解决,用三重循环遍历他x,y位置上的所有取值,根据y 筛选,如果筛选中有一个满足条件,那么证明所给数据条件是成立的,如果全部筛选完了,也没有一个满足条件的,就证明所给数据条件不成立。
代码:
时间复杂度o(tn)
#include <iostream>
using namespace std;
const int N=5;
struct edge
{int a,b,c;
} a[N];
int b[N];
int n;
int solve()
{for(int i=0;i<n;i++){int x=a[i].a,y=a[i].b,z=a[i].c;if(z==1){if(b[x]<b[y]) continue;else return 0;}else{if(b[x]>=b[y]) continue;else return 0;}}return 1;
}int main()
{int t;cin>>t;while (t--){int i,j,k;cin>>n;for(int z=0;z<n;z++){cin>>i>>j>>k;a[z]={i,j,k};}int res=0;for(int i=1;i<=3;i++) for(int j=1;j<=3;j++) for(int k=1;k<=3;k++){b[1]=i,b[2]=j,b[3]=k;res|=solve(); // |= 等于 两个数取之后,再赋值}if(res)cout<<"Yes"<<"\n";else cout<<"No"<<"\n";}return 0;
}思路2:
如果本题不使用暴力做法的话,可以把数据想象成一个图,起始点是x,终止点是y,建立一条以w为权值的边,然后开始遍历建图,如果存在一个不满足题目要求的边(即建不成我们想要的图)就输出NO 如果建成了(都满足条件)就输出YES,
本题难点就是不满足题目要求的边都是什么,是否完整。
当x向y建边时,边权是w
1. 重边冲突 即 图中已经有了一条 x->y w为1-w的边,此时失败
2. 传递冲突,即 图中已经有了一条x->x^y为1-w的边,x^y->y为1-w的边,此时根据传递性x->y的边边权应该是1-w,这就和的第一种冲突一样了,此时失败。
注:1^2=3,2^3=1, 1^3=2,一种小技巧, 仅对于1、2、3。
3. 自环 当 x==y,且w==1 时,因为当w==1时,根据题意时x<y 显然如果x==y ,该条件不成立
4.二元环 当存在一条y->x w=1的边时,x->y,w=1 不成立
5.三元环 当存在一条 y->x^y w=1,x^y->xw=1 的边是就是存在一条y->x w=1 此时和二元环一样,x->y ,w=1 不成立
代码:
时间复杂度o(tnlogn)
#include <iostream>
#include <array>
#include <set>using namespace std;
const int N=5;
struct edge
{int a,b,c;
} a[N];
int b[N];
int n;
int solve()
{set<array<int,3>> s;int n;cin>>n;for(int i=0;i<n;i++){int a,b,c;cin>>a>>b>>c;s.insert({a,b,c});}for(auto q:s ){int x=q[0],y=q[1],w=q[2];//重边冲突if(s.count({x,y,1-w})){puts("No");return 0 ;}//传递冲突if(s.count({x,x^y,1-w}) && s.count({x^y,y,1-w})){puts("No");return 0 ;}//自环xif(s.count({x,y,1}) && x==y && w==1){puts("No");return 0 ;}//二元环if(s.count({y,x,1}) && w==1){puts("No");return 0 ;}//三元环if(s.count({x,x^y,1}) && s.count({x^y,y,1}) && w==1){puts("No");return 0 ;}}puts("Yes");return 0;
}int main()
{int t;cin>>t;while (t--){solve();}return 0;
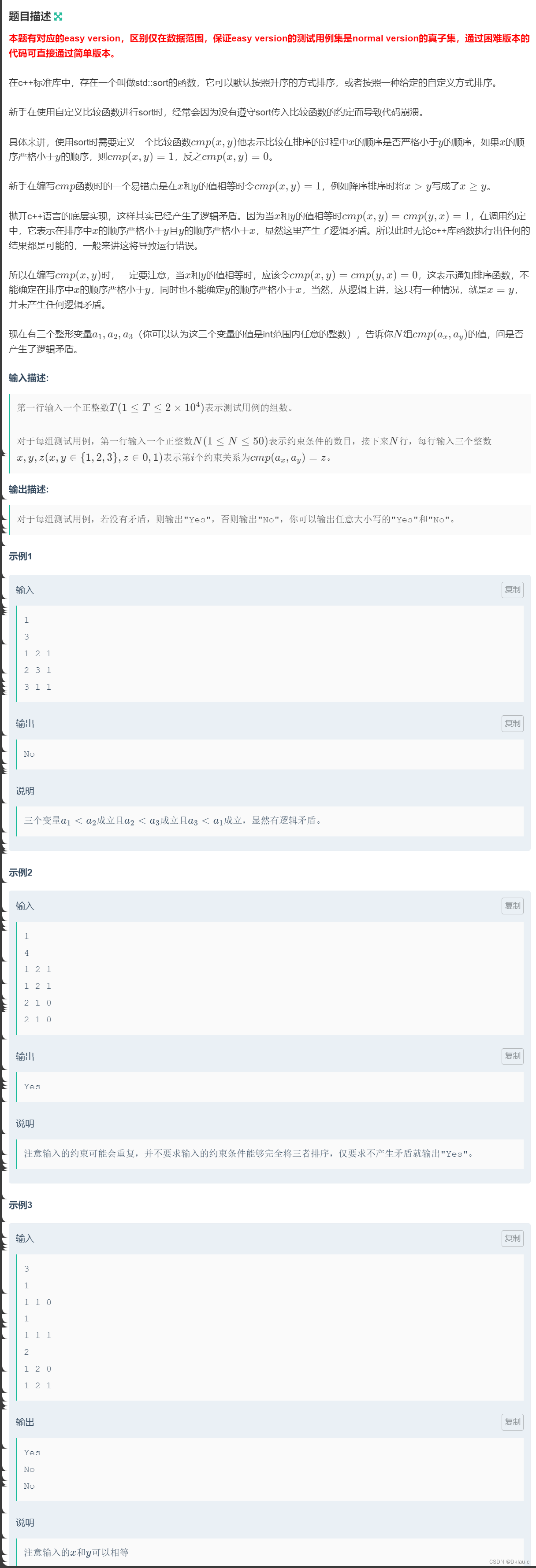
}H题:智乃的比较函数(normal version)
思路:
本题与G题仅在N的范围不同,本题N的范围最大是50,两种方法时间复杂度上也都能过,代码,思路就和上题一样。