目录
1.一元线性回归的数学原理
2.一元线性回归的代码实现
2.1需要安装sklearn库
2.2绘制离散点图
2.3引入Scikit-Learn库搭建模型
2.4 模型预测
2.5 模型可视化
摘要:线性回归模型是利用线性拟合的方式来探寻数据背后的规律,如下图所示,就是通过搭建线性回归模型来寻找这些散点(也称样本点)背后的趋势线(也称回归曲线),而通过这个回归曲线我们就能进行一些简单的预测分析或因果关系分析。
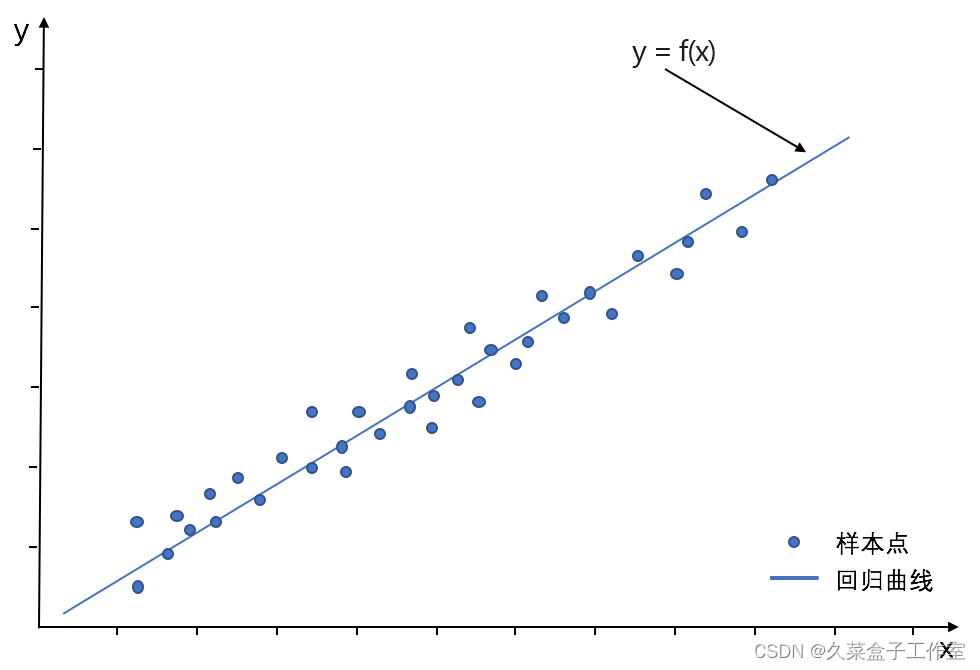
线性回归中,我们根据特征变量(也称自变量)来对反应变量(也称因变量)进行预测,根据特征变量的个数可将线性回归模型分为一元线性回归和多元线性回归。
通过一个特征变量:工作年限对收入进行预测,就属于一元线性回归;
通过多个特征变量:工作年限、行业、所在城市等对收入进行预测,就属于多元线性回归。
1.一元线性回归的数学原理
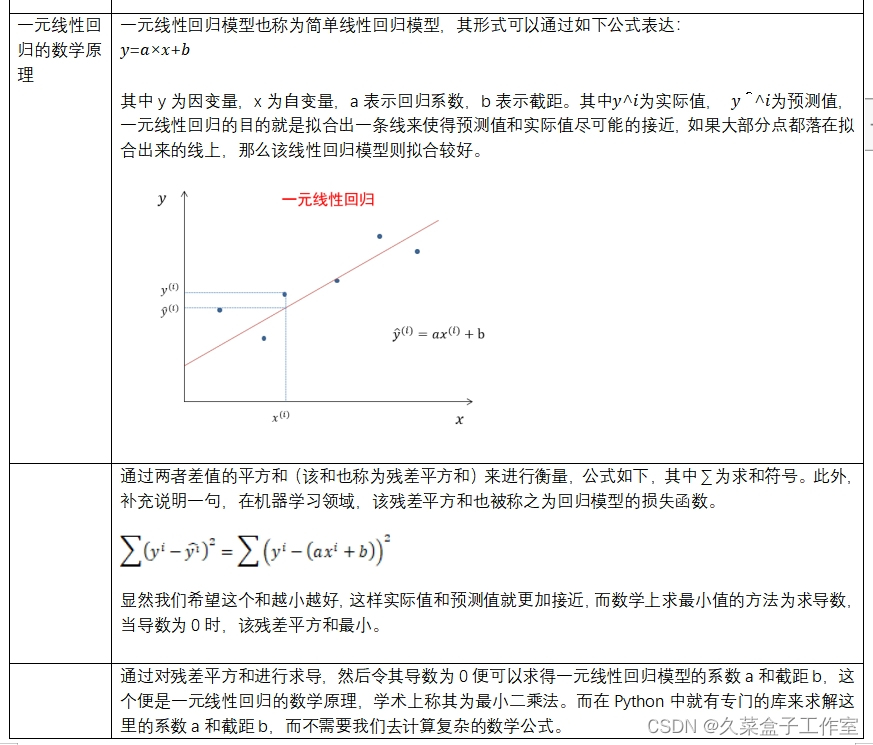
2.一元线性回归的代码实现
2.1需要安装sklearn库
sklearn是scikit-learn的简称,是一个基于Python的第三方模块。sklearn库集成了一些常用的机器学习方法,在进行机器学习任务时,并不需要实现算法,只需要简单的调用sklearn库中提供的模块就能完成大多数的机器学习任务。sklearn库是在Numpy、Scipy和matplotlib的基础上开发而成的,因此需要先安装这些依赖库。
安装顺序:
Numpy库
Scipy库
matplotlib库
sklearn库
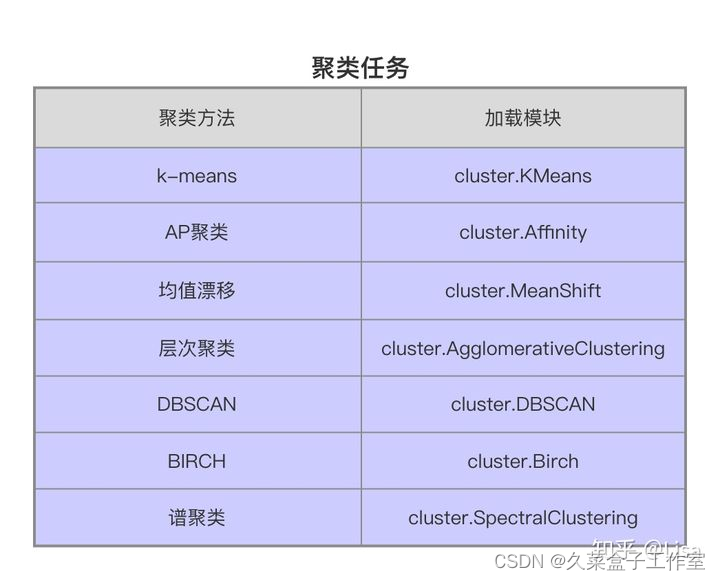
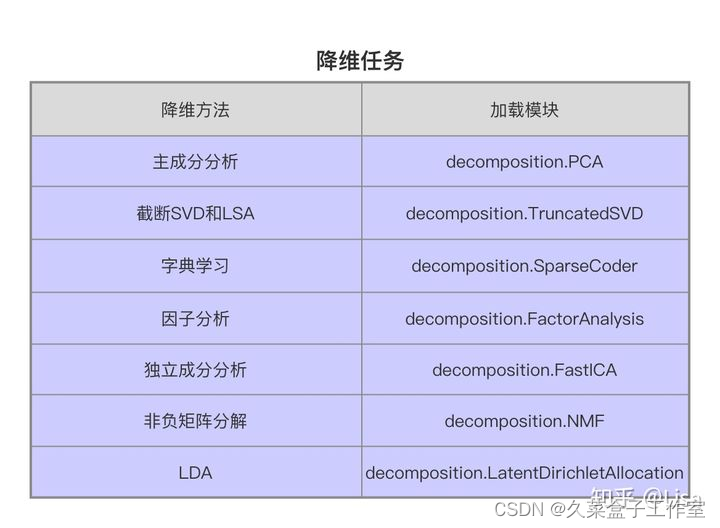
sklearn共分为6大部分,分别用于完成分类任务,回归任务,聚类任务,降维任务,模型选择以及数据的预处理。


2.2绘制离散点图
import matplotlib.pyplot as plt# 自变量要写成二维结构(列表),大列表内有小列表# 符合多元回归逻辑# 因为因变量y可能对应多个自变量x# 例如三个特征变量:[[1, 2, 3], [2, 4, 5], [4, 6, 8], [5, 7, 9]]x = [[1], [2], [4], [5]]y = [2, 4, 6, 8]# 显示离散点plt.scatter(x, y)plt.show()
2.3引入Scikit-Learn库搭建模型
# 引入线性回归相关模型LinearRegressionfrom sklearn.linear_model import LinearRegression# 构造一个初始的线性回归模型,并命名为regrregr = LinearRegression()# 完成模型搭建regr.fit(x, y)2.4 模型预测
# 使用predict()函数,括号内为自变量
# 自变量需要写成二维结构形式
# 获得的预测结果y为一个一维数组
y = regr.predict([[1.5]])print(y)y = regr.predict([[1.5], [2.5], [4.5]])print(y)显示:
[2.9]
[2.9 4.3 7.1]
2.5 模型可视化
print('系数a:' + str(regr.coef_[0]))
print('截距b:' + str(regr.intercept_))显示:
系数a:1.4000000000000004
截距b:0.79999999999999892.6 线性回归方程构造
# 通过coef_和intercept_属性获得系数、截距
# coef_得到的是一个列表,取编号0,就是取第一个数据,为系数
# intercept_就是数字, 没有列表
print('系数a:' + str(regr.coef_[0]))
print('截距b:' + str(regr.intercept_))显示:
系数a:1.4000000000000004
截距b:0.7999999999999989显示:
系数a:1.4000000000000004
截距b:0.7999999999999989