文章目录
- 前言
- 参考目录
- 学习笔记
- 0:符号表 ST 的回顾
- 1:2-3 查找树
- 1.1:定义
- 1.2:2-3 树 demo 演示
- 1.2.1:搜索:成功命中
- 1.2.2:搜索:未命中
- 1.2.3:插入:2-节点
- 1.2.4:插入:3-节点 1
- 1.2.5:插入:3-节点 2
- 1.2.6: 插入:2-3 树构造
- 1.3:2-3 树局部变换
- 1.4:2-3 树全局性质
- 1.5:2-3 树性能
- 1.6:符号表实现小结
- 1.7:2-3 树实现?
前言
由于本章节的内容很多,所以分成了上下两篇,本篇比较简单,主要内容是 2-3 树 以及其相关的 API 操作介绍。
在学习本章节前,建议先学习上一章节关于 BST(二叉搜索树)的内容。
参考目录
- B站 普林斯顿大学《Algorithms》视频课
(请自行搜索。主要以该视频课顺序来进行笔记整理,课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。) - 微信读书《算法(第4版)》
(本文主要内容来自《3.3 平衡查找树》) - 官方网站
(有书本配套的内容以及代码)
学习笔记
注1:下面引用内容如无注明出处,均是书中摘录。
注2:所有 demo 演示均为视频 PPT demo 截图。
注3:如果 PPT 截图中没有翻译,会在下面进行汉化翻译,因为内容比较多,本文不再一一说明。
开篇的时候,Prof. Sedgewick 是这样介绍本章节的:
Which will lead us to an ultimate symbol table implementation that can provide fast performance for all the simulative options we’ve looked at, guaranteed.
这将引导我们得到一个终极符号表实现,能够确保为迄今为止我们所探讨的所有模拟选项提供快速的性能。
由此可见本章节的重要性,确实在实际中也有很多应用,在下篇的后面会有简单总结。
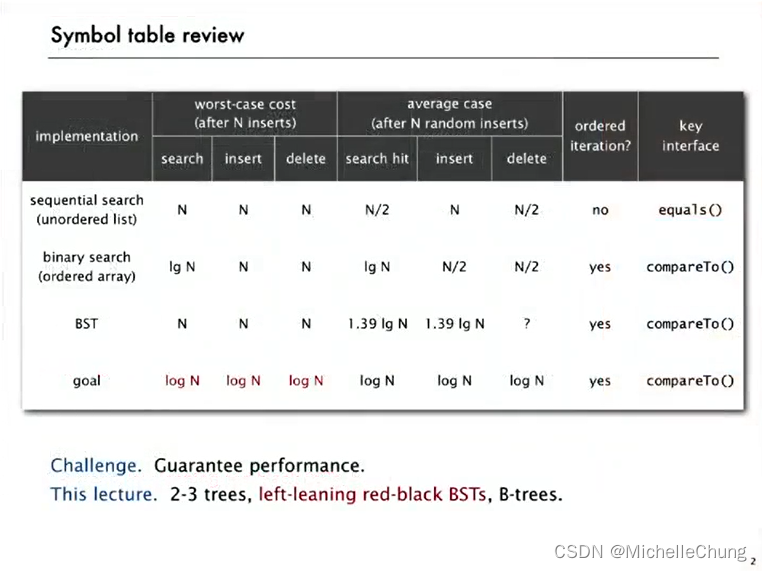
0:符号表 ST 的回顾
挑战:保证性能。
本课时:2-3树、左倾红黑树、B树。
(下篇将介绍左倾红黑树以及B树的相关内容)
1:2-3 查找树
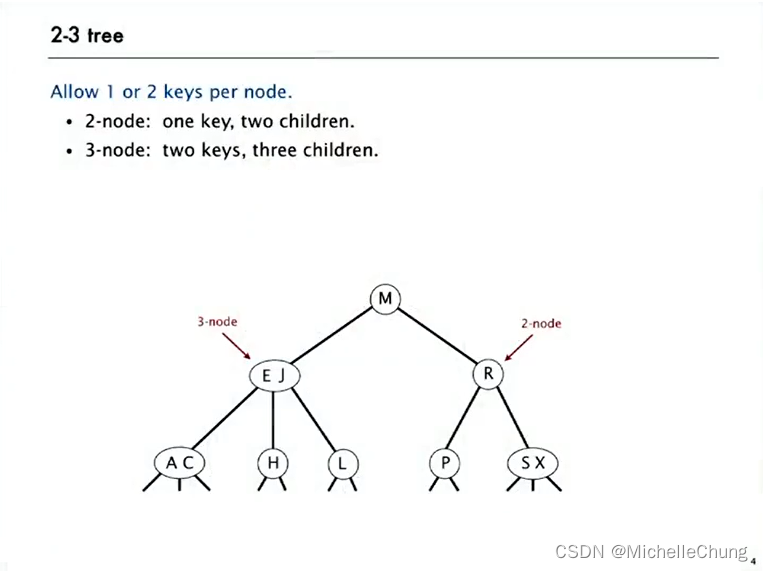
1.1:定义
每个节点允许 1 或 2 个键。
2-节点:一个键,两个子节点。
3-节点:两个键,三个子节点。
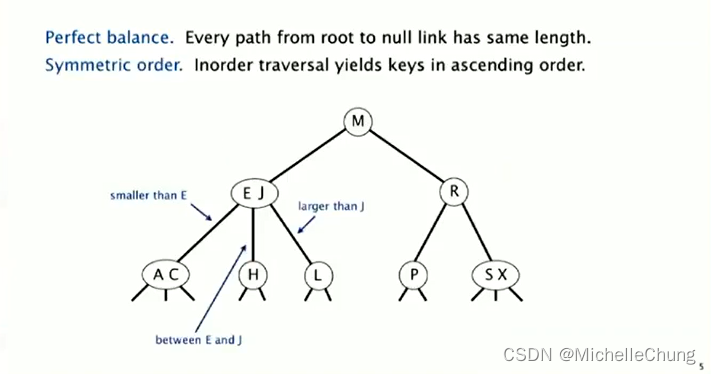
完美平衡:从根节点到空链接的所有路径具有相同的长度。
对称顺序:中序遍历产生的键按升序排列。
这里插入一下,在刚开始的时候,没有很懂为什么不能 4 个节点,所以就问了一下通义:
Q:为什么 2-3 树,只能3节点不能4节点?
A: 2-3树的设计初衷是为了保持数据结构的自平衡,即在进行插入和删除操作时能够通过局部调整来维护节点间的平衡条件,从而确保查找、插入和删除等基本操作的时间复杂度维持在O(log n)。在2-3树中,节点可以是2节点或3节点:
- 2节点:包含1个键值对和2个子指针(左子树和右子树)。
- 3节点:包含2个键值对和3个子指针。
之所以设计成只有2节点和3节点,而不是直接引入4节点,是因为2-3树的平衡是通过将满的3节点分裂为两个2节点实现的,这样就能保证任何路径上的节点数量大致相等,进而维持了树的高度均衡。如果允许4节点存在,那么在处理插入和删除时需要更复杂的机制来保持平衡,而这种平衡机制在2-3树的基础上进一步扩展形成了2-3-4树(也称为2-4树),其中4节点可以容纳3个键值对和4个子指针。
在2-3-4树中,当一个4节点由于插入或删除变得不平衡时,可以通过拆分或合并节点的方
式重新达到平衡状态。而在经典的2-3树中,则不允许直接出现4节点以简化平衡过程。
1.2:2-3 树 demo 演示
搜索:
- 将搜索键与节点中的键进行比较。
- 找到包含搜索键的区间。
- 沿着关联的链接(递归地)继续搜索。
书本中的说明:
要判断一个键是否在树中,我们先将它和根结点中的键比较。如果它和其中任意一个相等,查找命中;否则我们就根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归地继续查找。如果这是个空链接,查找未命中。
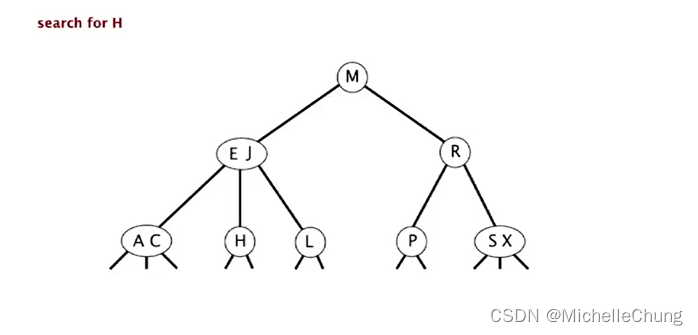
1.2.1:搜索:成功命中
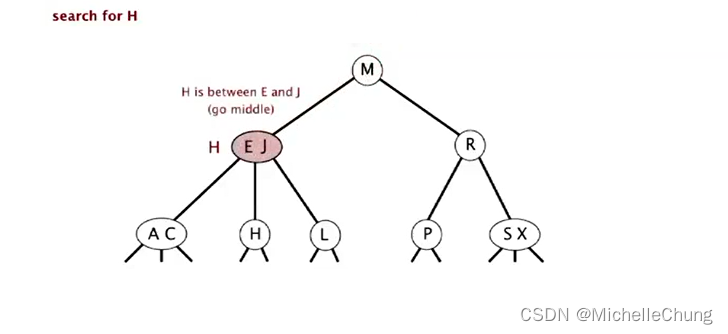
搜索 H:
初始状态:
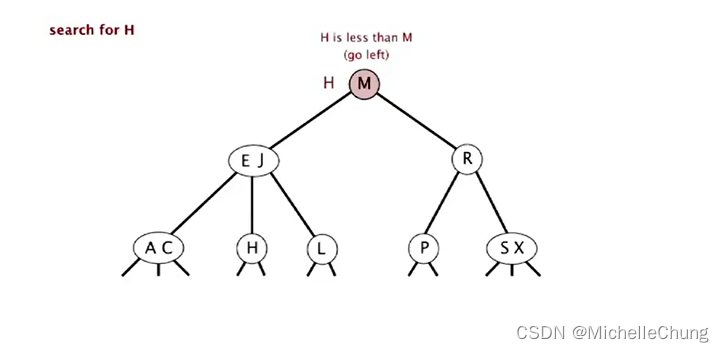
与根节点 M 比较(更小),左移:
与节点 M 左子树节点 E J 比较(介于两者之间),走中路:
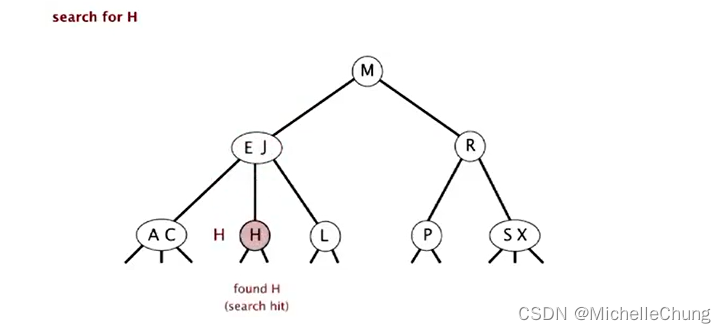
与节点 E J 中子树节点 H 比较(相等),搜索命中:
1.2.2:搜索:未命中
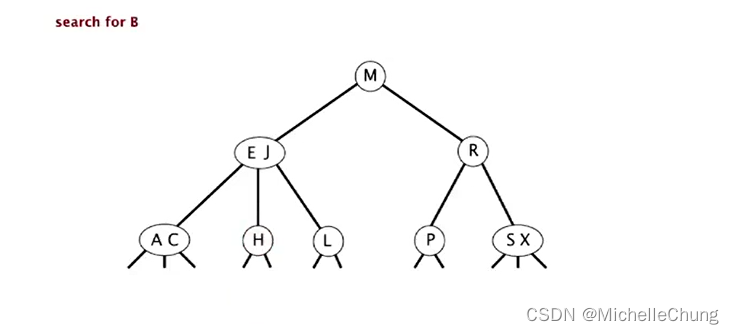
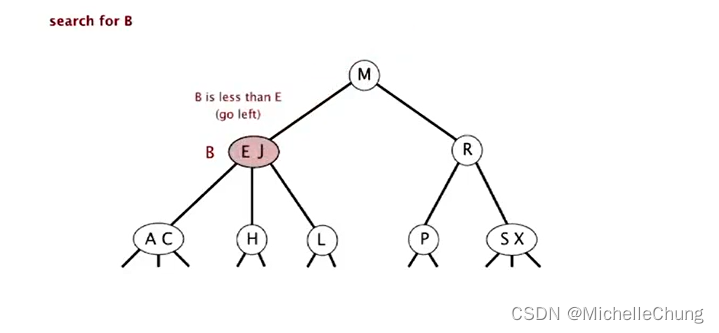
搜索 B:
初始状态:
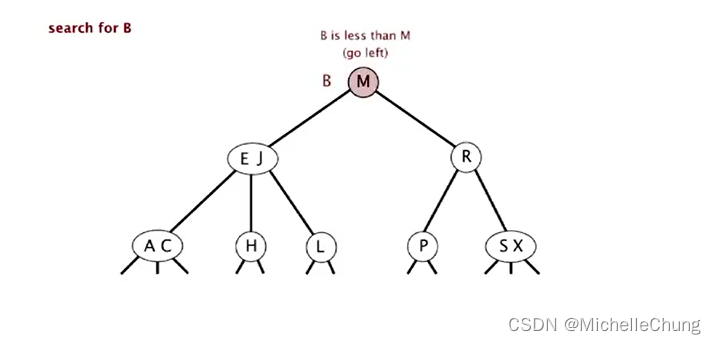
与根节点 M 比较(更小),左移:
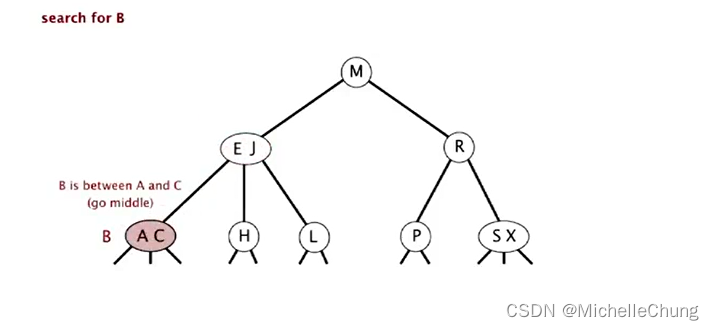
与节点 M 左子树节点 E J 比较(更小),左移:
与节点 E J 左子树节点 A C 比较(介于两者之间),走中路:
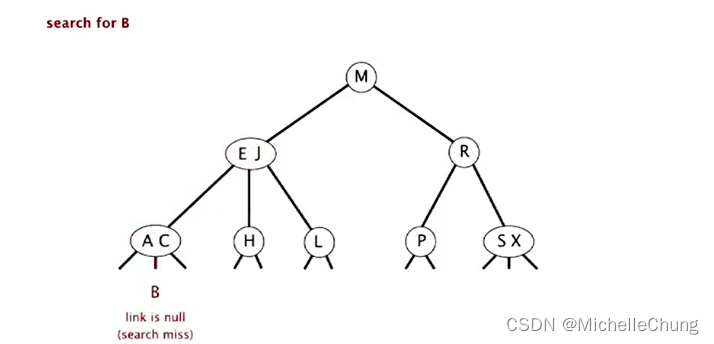
B 走中路为空链接,查找未命中(并返回null):
1.2.3:插入:2-节点
插入操作和普通 BST 类似,不同的是要调整 2-节点和 3-节点,让树保持完美的平衡。
在底部插入一个 2-节点:
- 按照常规方法搜索键。
- 用 3-节点替换 2-节点。
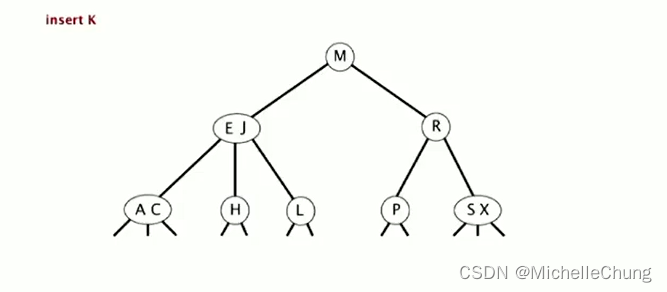
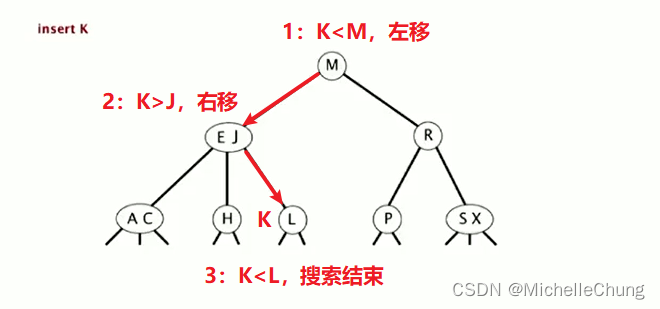
插入 K:
初始状态:
搜索阶段步骤类似,遇到空链接则结束,K 完整移动路线图:
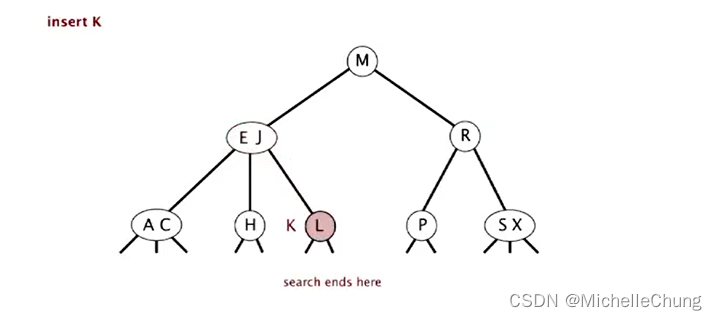
搜索完成:
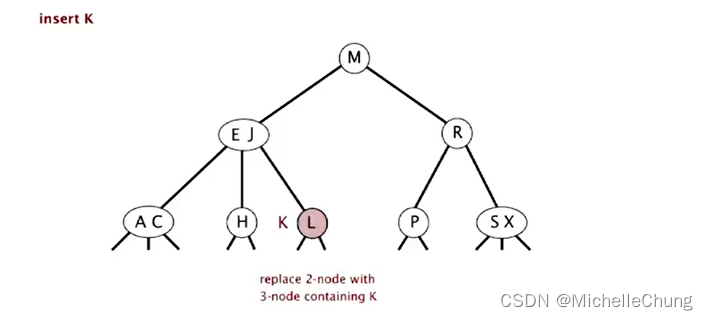
将 2-节点改为 3-节点,双链改为三链,插入完成:
1.2.4:插入:3-节点 1
在底部插入一个 3-节点:
- 向 3-节点添加新键以创建临时的 4-节点。
- 将 4-节点中的中间键移至其父节点。
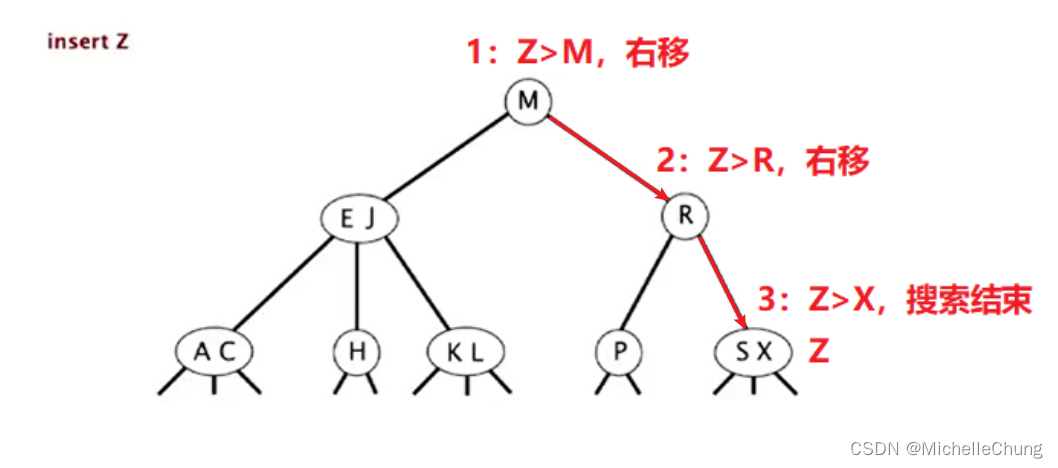
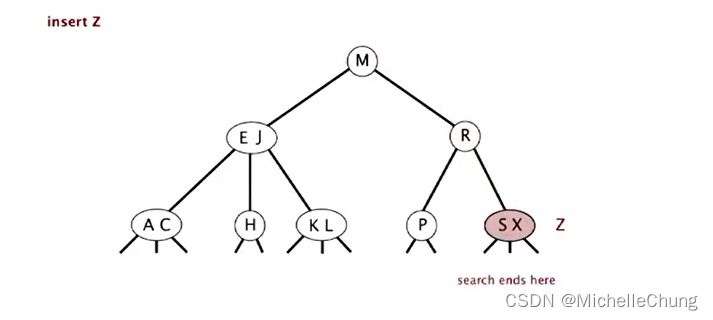
插入 Z:
初始状态:
搜索阶段步骤类似,遇到空链接则结束,Z 完整移动路线图:
搜索完成:
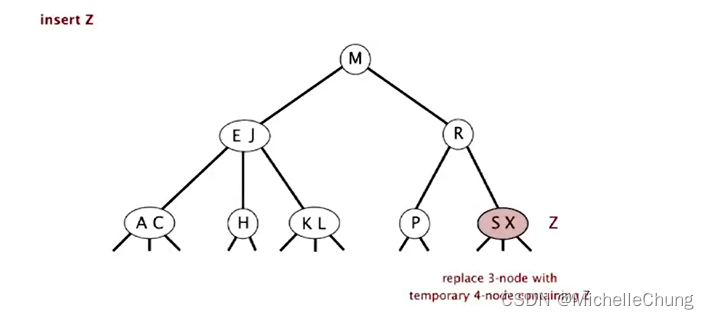
将 3-节点改为 临时 4-节点,三链改为 临时四链:
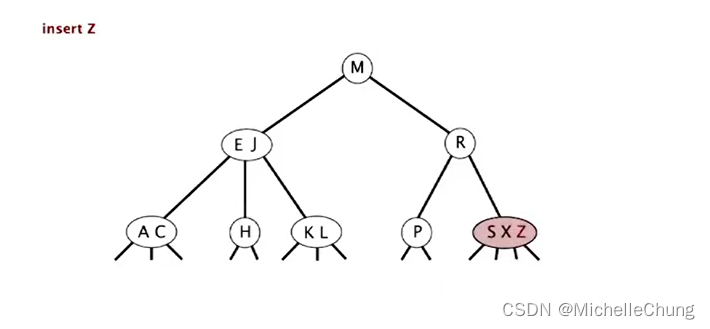
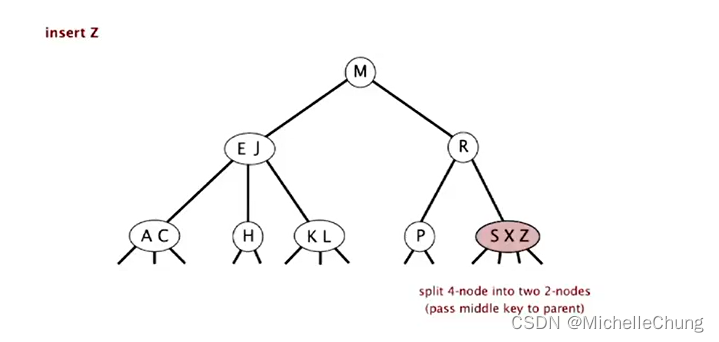
对临时 4-节点 分解(拆分):
- 4-节点中键移动到父节点,父节点由 2-节点变为 3-节点,双链变成三链
- 右子树(S Z)拆分,由3-节点变为 2-节点
- 插入完成
1.2.5:插入:3-节点 2
在底部插入一个 3-节点:
- 向 3-节点添加新键以创建临时的 4-节点。
- 将 4-节点中的中间键移至其父节点。
- 如有必要,沿树向上重复此过程。
- 如果到达根节点且该根节点是 4-节点,则将其拆分为三个 2-节点。
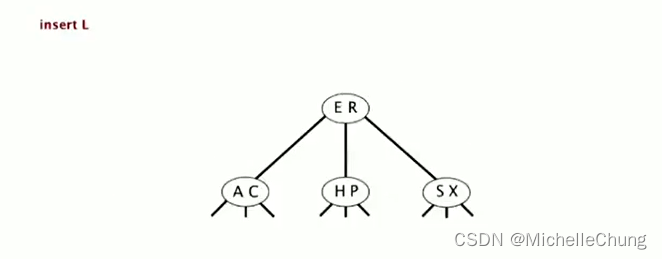
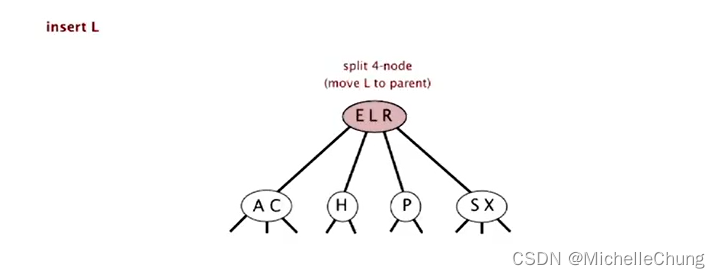
插入 L:
初始状态:
这里省略了搜索阶段,只讲解分解阶段。
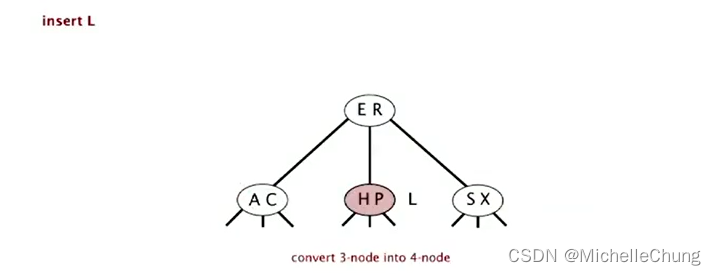
在底部 3-节点 H P 插入节点 L:
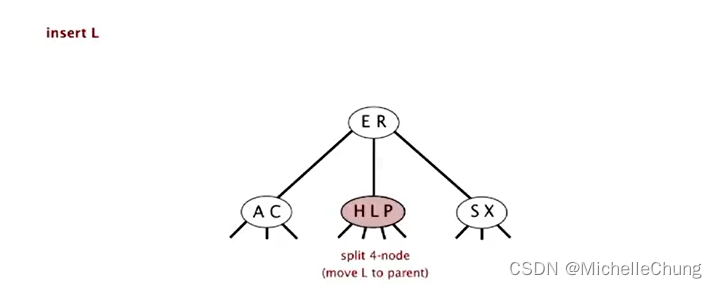
临时 4-节点 H L P 分解:
- 中键 L 移动至父节点
- 3-节点 H P 分为 2 个 2-节点
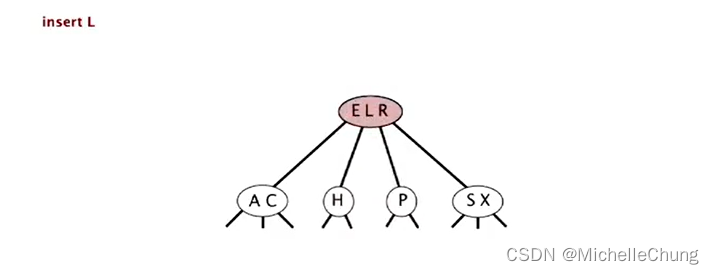
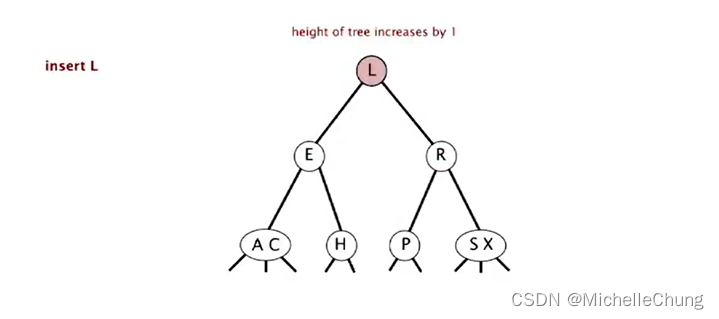
再次分解 临时 4-节点 E L R:
- 中键 L 上移变为新的根节点
- 3-节点 E R 分为 2 个 2-节点
- 树高 +1
- 插入完成(不得不说,妙哇~!!!)
1.2.6: 插入:2-3 树构造
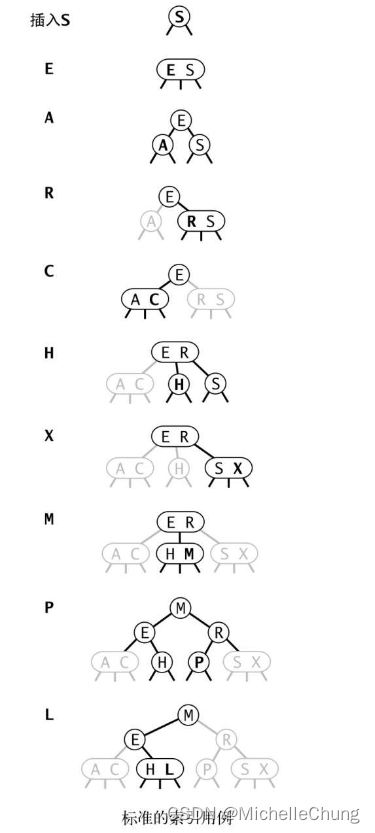
步骤太长,这里直接用书里的步骤插图。
图3.3.10 2-3树的构造轨迹
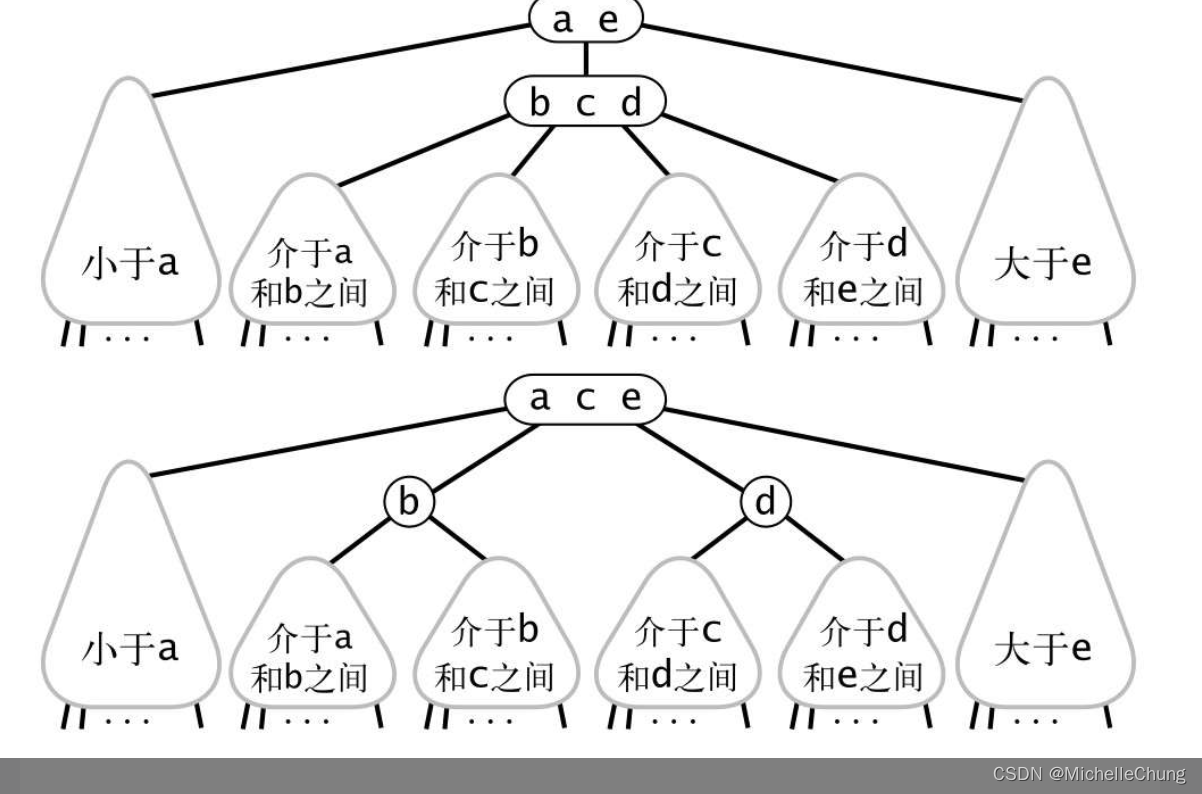
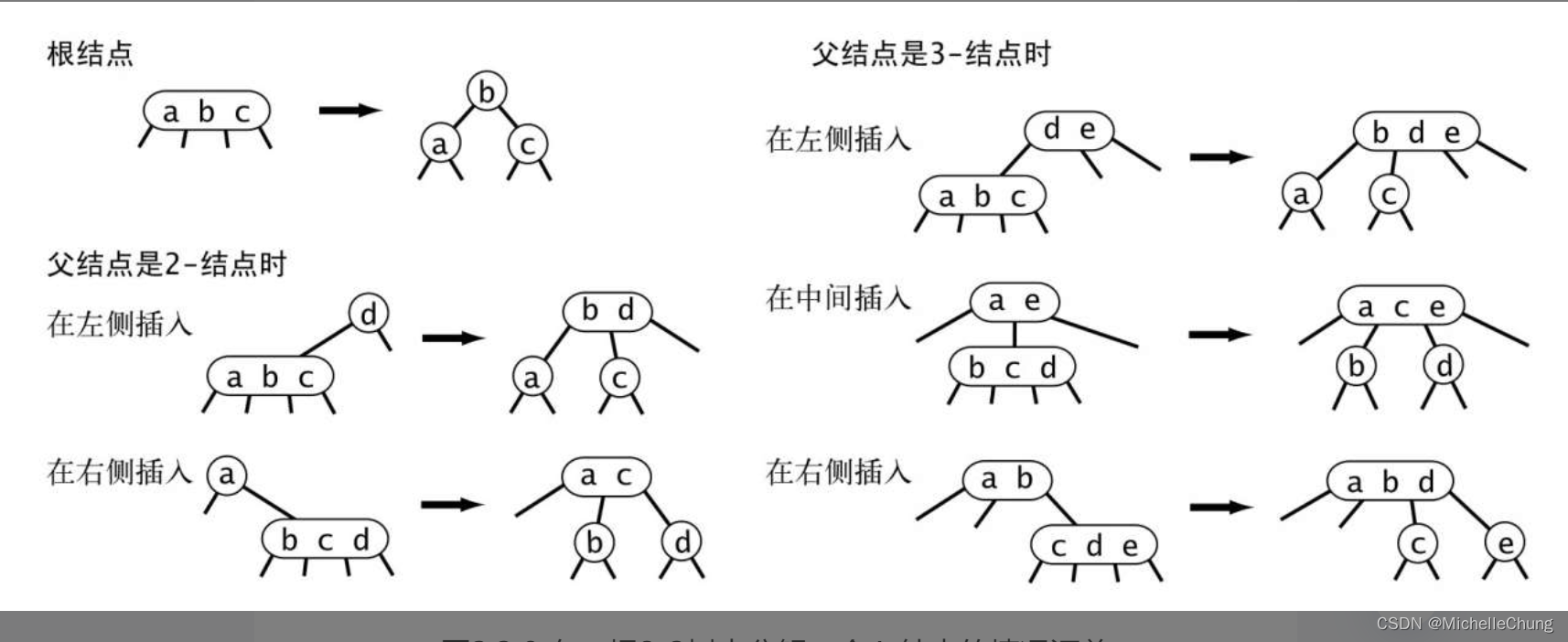
1.3:2-3 树局部变换
图3.3.9 4-结点的分解是一次局部变换,不会影响树的有序性和平衡性
1.4:2-3 树全局性质
不变性:保持对称有序和完美平衡。
证明:每次转换都保持了对称有序和完美平衡。
图3.3.8 在一棵 2-3 树中分解一个 4-结点的情况汇总
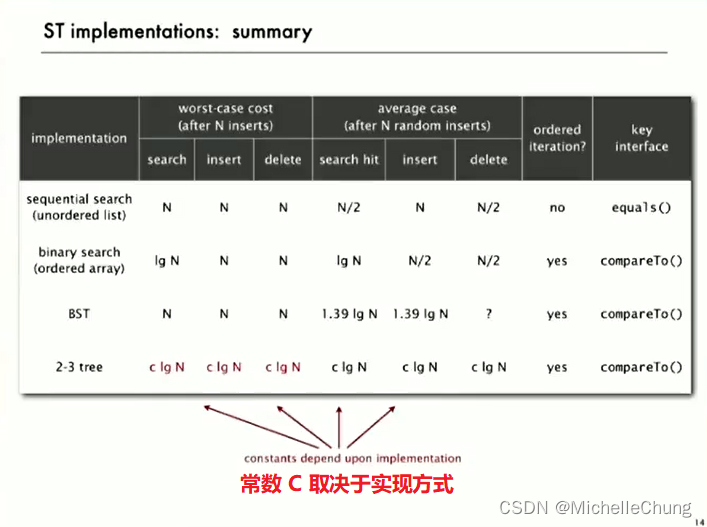
1.5:2-3 树性能
1.6:符号表实现小结
1.7:2-3 树实现?
直接实现较为复杂,原因在于:
- 维护多种节点类型十分繁琐。
- 需要多次比较才能向下遍历树。
- 为了分解 4-节点,需要回溯至父节点。
- 针对分解操作存在大量不同情况。
归根结底,虽然可以实现,但有更好的方法。
(未完待续)