曾梦想执剑走天涯,我是程序猿【AK】
目录
- 简述概要
- 知识图谱
- 1.什么是逻辑回归?
- 2.逻辑回归有哪些应用?
- 3.回归分析如何工作?
- 4.逻辑回归模型如何工作?
- 5.逻辑回归分析有哪些类型?
- 6.逻辑回归与其他机器学习技术相比如何?
简述概要
了解逻辑回归
知识图谱
1.什么是逻辑回归?
逻辑回归是一种数据分析技术,它使用数学来找出两个数据因子之间的关系。然后,使用此关系根据其中一个因子预测另一个因子的值。预测结果的数量通常是有限的,比如是或否。
例如,假设您想猜测您的网站访客是否会点击购物车中的结账按钮。逻辑回归分析着眼于过去的访客行为,例如在网站上花费的时间和购物车中的商品数量。它确定,在过去,如果访客在网站上停留的时间超过五分钟,并且向购物车中添加了三件以上的商品,他们就会点击结账按钮。利用这些信息,逻辑回归函数可以预测新网站访客的行为。
为什么逻辑回归很重要?
逻辑回归是人工智能和机器学习(AI/ML)领域的一项重要技术。机器学习模型是可以训练的软件程序,无需人工干预即可执行复杂的数据处理任务。使用逻辑回归构建的机器学习模型可帮助组织从其业务数据中获得切实可行的见解。他们可以利用这些见解进行预测分析,以降低运营成本、提高效率并加快扩展速度。例如,企业可以发现提高员工保留率或打造更有利可图的产品设计的模式。
下面,我们列出了使用逻辑回归相对于其他机器学习技术的一些好处。
简易性
逻辑回归模型在数学上不像其他机器学习方法那么复杂。因此,即使您的团队中没有人具备深入的机器学习专业知识,您也可以实施逻辑回归模型。
速度
逻辑回归模型可以高速处理大量数据,因为它们需要的计算能力(如内存和处理能力)较少。这使得它们非常适合那些从机器学习项目入手以快速取得成就的组织。
灵活性
您可以使用逻辑回归来查找具有两个或更多有限结果的问题的答案。您还可以使用它来预处理数据。例如,您可以使用逻辑回归将具有较大值范围的数据(例如银行交易)整理为较小的有限值范围。然后,您可以使用其他机器学习技术来处理这个较小的数据集,以进行更准确的分析。
可见性
与其他数据分析技术相比,逻辑回归分析使开发人员能够更好地了解内部软件进程。由于计算不那么复杂,问题排查和纠错也更容易。
2.逻辑回归有哪些应用?
逻辑回归在许多不同的行业都有一些实际应用。
制造业
制造企业使用逻辑回归分析来估计机械零件故障的概率。然后,他们根据此估计规划维护计划,以最大限度地减少将来的故障。
医疗保健
医学研究人员通过预测患者患病的可能性来规划预防性护理和治疗。他们使用逻辑回归模型来比较家族史或基因对疾病的影响。
金融
金融公司必须分析金融交易中的欺诈行为,并评估贷款申请和保险申请的风险。逻辑回归模型适用于这些问题,因为它们具有离散的结果,例如高风险或低风险,欺诈性或非欺诈性。
市场营销
在线广告工具使用逻辑回归模型来预测用户是否会点击广告。因此,营销人员可以分析用户对不同词语和图像的反应,制作出吸引客户的高质量广告。
3.回归分析如何工作?
逻辑回归是数据科学家在机器学习(ML)中常用的几种不同的回归分析技术之一。要理解逻辑回归,我们必须首先了解基本的回归分析。下面,我们使用线性回归分析的示例来演示回归分析的工作原理。
确定问题
任何数据分析都从一个业务问题开始。对于逻辑回归,您应该将问题框定为获得特定的结果:
- 雨天是否会影响我们的月销售额?(是或否)
- 客户正在执行哪种类型的信用卡活动?(授权、欺诈或潜在欺诈)
收集历史数据
确定问题后,您需要确定所涉及的数据因子。然后,您将收集所有因子过去的数据。例如,要回答上面显示的第一个问题,您可以收集过去三年中每个月的雨天数和月度销售数据。
训练回归分析模型
您将使用回归软件处理历史数据。该软件将处理不同的数据点,并使用方程式以数学方式将它们关联起来。例如,如果三个月的雨天数为 3、5 和 8,而这三个月的销售数量分别为 8、12 和 18,回归算法会使用以下方程式将这些因子关联起来:
销售数量 = 2*(雨天数)+ 2
预测未知值
对于未知值,软件使用方程式进行预测。如果您知道七月会下雨六天,该软件会将七月的销售值估计为 14。
4.逻辑回归模型如何工作?
要理解逻辑回归模型,我们首先要了解方程式和变量。
方程式
在数学中,方程式给出了两个变量之间的关系:x 和 y。您可以使用这些方程式或函数,通过输入不同的 x 和 y 值来沿 x 轴和 y 轴绘制图形。例如,如果绘制函数 y = 2*x 的图形,则会得到一条直线,如下所示。因此,该函数也称为线性函数。

变量
在统计中,变量是其值不同的数据因子或属性。对于任何分析,某些变量是自变量或解释变量。这些属性是结果的原因。其他变量是因变量或响应变量;它们的值取决于自变量。通常,逻辑回归通过查看两个变量的历史数据值来探索自变量如何影响一个因变量。
在上面的示例中,x 被称为自变量、预测变量或解释变量,因为它具有已知值。y 被称为因变量、结果变量或响应变量,因为其值未知。
逻辑回归函数
逻辑回归是一种统计模型,它使用数学中的逻辑函数或 logit 函数作为 x 和 y 之间的方程式。Logit 函数将 y 映射为 x 的 sigmoid 函数。
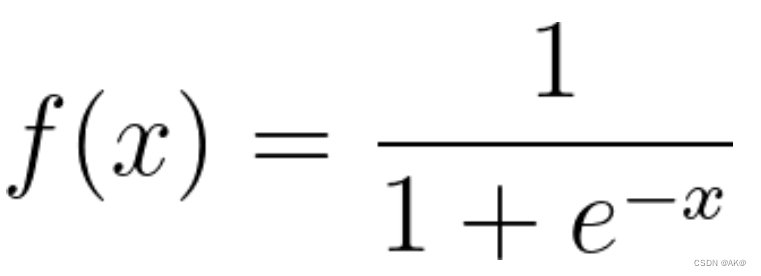
如果绘制此逻辑回归方程式,您将得到如下所示的 S 曲线。
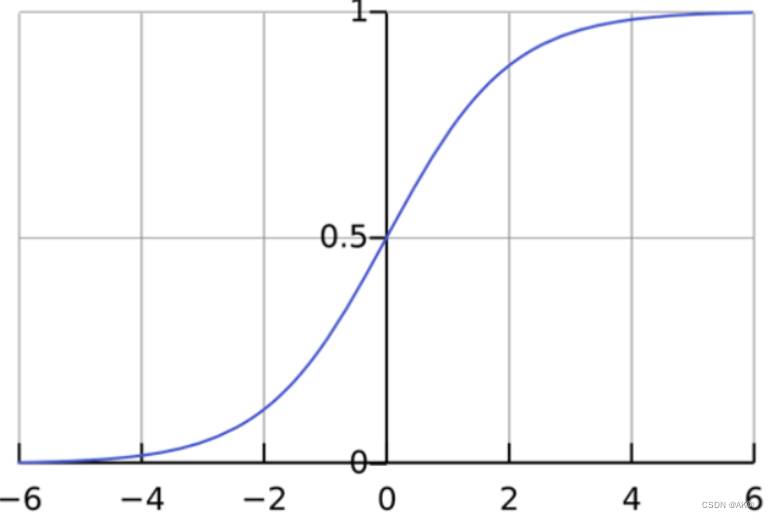
如您所见,logit 函数仅返回因变量介于 0 和 1 之间的值,而不考虑自变量的值。这就是逻辑回归估计因变量值的方式。逻辑回归方法还可以对多个自变量和一个因变量之间的方程式进行建模。
使用多个自变量进行逻辑回归分析
在许多情况下,多个解释变量会影响因变量的值。要对此类输入数据集建模,逻辑回归公式假设不同自变量之间存在线性关系。您可以修改 sigmoid 函数并按如下公式计算最终输出变量
y = f(β0 + β1x1 + β2x2+… βnxn)
符号 β 表示回归系数。当您给它一个其中包含因变量和自变量的已知值的足够大的实验数据集时,logit 模型可以反向计算这些系数值。
对数赔率
Logit 模型还可以确定成功与失败的比率或对数赔率。例如,如果您和朋友一起玩扑克,并且赢了十场比赛中的四场,那么您的获胜赔率是 4/6,或者六分之四,这是您成功与失败的比率。另一方面,获胜的概率是十分之四。
从数学上讲,您的概率赔率是 p/(1 - p),您的对数赔率是 log (p/(1 - p))。您可以将逻辑函数表示为对数赔率,如下所示:
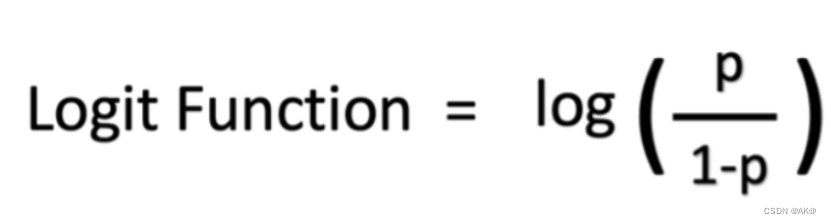
5.逻辑回归分析有哪些类型?
有三种基于因变量结果的逻辑回归分析方法。
二元逻辑回归
二元逻辑回归适用于只有两种可能结果的二进制分类问题。因变量只能有两个值,例如“是”和“否”或 0 和 1。
即使逻辑函数计算的值范围介于 0 和 1 之间,二元回归模型也会将答案四舍五入到最接近的值。通常,小于 0.5 的答案四舍五入为 0,大于 0.5 的答案四舍五入为 1,因此逻辑函数返回二进制结果。
多项式逻辑回归
只要结果数量有限,多项式回归就可以分析具有多种可能结果的问题。例如,它可以根据人口数据预测房价是否会上涨 25%、50%、75% 或 100%,但它无法预测房屋的确切价值。
多项式逻辑回归的工作原理是将结果值映射到 0 和 1 之间的不同值。由于逻辑函数可以返回一系列连续数据,如 0.1、0.11、0.12 等,因此多项式回归还会根据最接近的可能值对输出进行分组。
有序逻辑回归
有序逻辑回归或有序 logit 模型是一种特殊的多项式回归,用于解决数字代表等级而不是实际值的问题。例如,您可以使用有序回归来预测调查问题的答案,该问题要求客户根据数值(例如他们在一年中向您购买的商品数量)将您的服务评为差、一般、良好或优秀。
6.逻辑回归与其他机器学习技术相比如何?
两种常见的数据分析技术是线性回归分析和深度学习。
线性回归分析
如上所述,线性回归使用线性组合对因变量和自变量之间的关系进行建模。线性回归方程式为
y= β0X0 + β1X1 + β2X2+… βnXn+ ε,其中,β1 至 βn 和 ε 是回归系数。
逻辑回归与线性回归
线性回归通过使用一组给定的自变量来预测连续因变量。连续变量可以有一系列值,例如价格或年龄。因此,线性回归可以预测因变量的实际值。它可以回答诸如“10 年后大米的价格会是多少?”这样的问题。
与线性回归不同,逻辑回归是一种分类算法。它无法预测连续数据的实际值。它可以回答诸如“10 年后大米的价格是否会上涨 50%?”这样的问题。
深度学习
深度学习使用模拟人脑的神经网络或软件组件来分析信息。深度学习计算是基于向量的数学概念。
逻辑回归与深度学习
与深度学习相比,逻辑回归复杂度更低,计算密集度也更低。更重要的是,由于深度学习计算的复杂性、机器驱动的性质,开发人员无法研究或修改深度学习计算。另一方面,逻辑回归计算是透明的,更容易进行问题排查。
推荐链接:
https://zhuanlan.zhihu.com/p/74874291
https://xie.infoq.cn/article/0fad8979012cdcd57344af1f6
---- 永不磨灭的番号:我是AK