1. 强化学习方法

1.1 动态规划法

动态规划方法是由Bellman 方程转化而来，通过修正Bellman 方程的规则，提高所期望值函数的近

似值。常用算法有两种：值迭代（Value Iteration）和策略迭代（Policy Iteration）（策略π、T 函

数和R函数已知）。

状态值函数更新：

Bellman最优方程：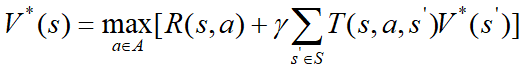

值迭代是在保证算法收敛的情况下，缩短策略估计的过程，每次迭代只扫描(sweep)了每个状态一

次。而策略迭代算法包含了一个策略估计的过程，而策略估计则需要扫描所有的状态若干次，其中

巨大的计算量直接影响了策略迭代算法的效率。

动态规划方法通过反复扫描整个状态空间，对每个状态产生可能迁移的分布，然后利用每个状态的

迁移分布，计算出更新值，并更新该状态的估计值，所以计算量需求会随状态变量数目增加而呈指

数级增长，从而造成“维数灾”问题。

1.2 蒙特卡罗方法

蒙特卡罗方法（Monte Carlo methods:MC）是一种模型无关(model free)的，解决基于平均样本回

报的强化学习问题的学习方法。(它用于情节式任务(episode task)，不需要知道环境状态转移概率

函数T和奖赏函数R，只需要智能体与环境从模拟交互过程中获得的状态、动作、奖赏的样本数据

序列，由此找出最优策略)。

MC算法的状态值函数更新规则为：

其中，Rt为t时刻的奖赏值，α为步长参数

1.3 时间差分学习方法

时间差分（Temporal-Difference,TD）学习方法是一种模型无关的算法，它是蒙特卡罗思想和动态

规划思想的结合，一方面可以直接从智能体的经验中学习，建立环境的动态信息模型，不必等到最

终输出结果产生之后，再修改历史经验，而是在学习过程中不断逐步修改。正因为这个特点使得

TD 方法处理离散序列有很大的优势。

2. 强化学习算法

到目前为止，研究者提出了很多强化学习算法，其中较有影响的有瞬时差分法(Temporal

Difference Algorithm)、Q-学习算法(Q-Learning Algorithm)、R-学习算法(R-Learning Algorithm)、

Sarsa算法、自适应评价启发算法(AHC)、分层强化学习(HRL)等等。其中，TD-算法和Q-学习算法

属于典型的模型无关法, 而Sarsa和Dyna-Q算法属于基于模型法。

2.1 顺时差分法TD

TD算法是Sutton 在1988 年提出的用于解决时间信度分配问题的著名方法。TD 方法能够有效的解

决强化学习问题中的暂态信用分配问题，可被用于评价值函数的预测。几乎所有强化学习算法中评

价值的预测法均可看作TD 方法的特例，以至于通常所指的强化学习实际上就是TD 类强化学习。

一步TD 算法，即TD (0) 算法，是一种自适应的策略迭代算法，又名自适应启发评价算法(Adaptive

Heuristic Critic，AHC)。所谓一步TD 算法，是指Agent 获得的瞬时报酬值仅回退一步，也就是说

只是修改了相邻状态的估计值。TD (0)的算法迭代公式为：

式中，β为学习率，V(st)为Agent在t时刻访问环境状态st估计的状态值函数，V(st+1)指Agent在t+1

时刻访问环境st+1估计的状态值函数，rt+1指Agent从状态st向状态st+1转移时获得的瞬间奖赏值。

学习开始时，首先初始化V值，然后Agent在st状态，根据当前决策确定动作at，得到经验知识和训

练例{st,at,st+1,rt+1}；其次根据经验知识，依据上式修改状态值函数，当Agent访问目标状态时，

算法终止一次迭代循环。算法继续从初始状态开始新的迭代循环，直至学习结束。

TD 算法可扩充到TD(λ)算法，即Agent 获得的瞬时报酬值可回退任意步。TD ( λ)算法的收敛速度有

很大程度上的提高。其迭代公式为：

式中，e(s)定义为状态s的选举度。其中e(s)可通过以下方式计算：

奖赏值向后传播t步。当前状态历史t步中，如果一个状态被多次访问，则其选举度e(s)越大，表明

其对当前奖赏值的贡献越大，并通过上式迭代修改。

TD(λ)算法较TD(0)算法在收敛速度有很大程度的提高，但是由于TD(λ)在递归过程中的每个时间步

要对所有的状态进行更新，当状态空间较大时，难以保证算法的实时性。

2.2 Q-学习算法

Q-学习可以看作一种增量式动态规划，它通过直接优化一个可迭代计算的动作值函数Q(s,a) ，来

找到一个策略使得期望折扣报酬总和最大的E(s)，而非TD 算法中的状态值V(s)，其中

E(s)=maxQ(s,a)。这样，Agent 在每一次的迭代中都需要考察每一个行为，可确保学习过程收敛。

其中Q(s,a)指状态s执行完动作a后希望获得的累积回报，它取决于当前的立即回报和期望的延时回

报。Q值得修改方法：

式中：r是当前的立即回报，γE(s')指示期望的延时回报，β代表学习率，她随学习的进步而逐渐变

小，直到为0，其满足β≤1。γ是一个对延时回报的折扣因子，γ越大，未来回报的比重越大，其满

足0≤γ。实际上，Q(s,a)的新值就是原Q值和新Q估计值(即r+γE(s'))的组合，组合的比例依赖于学习

率β。Q学习的一般步骤：

1）初始化  以随机或某种策略方式初始化所有的Q(s,a)，选择一种状态作为环境的初始状态。

2）观察当前环境状态，设为s；

3）执行该动作a；

4）设r为在状态s执行完动作a后所获得的立即回报；

5）根据式(3)更新Q(s,a)的值，同时进入下一新状态s'。

上述γ和β都是可调的学习参数，当β为1时，原有的Q(s,a)值对新Q值没有任何影响，学习率很高，

但容易造成Q值不稳定；若β为0时，则Q(s,a)保持不变，学习过程静止。并且Q的初值越靠近最优

值，学习的过程越短，即收敛得越快。Q-学习算法可最终收敛于最优值。

Q 函数的实现方法主要有两种方式：一种是采用查找（look-up）表法，也就是利用表格来表示Q

函数，另一种是采用神经网络来实现。

1) 采用查找（look-up）表法，也就是利用表格来表示Q 函数，表的大小等于S*A的笛卡儿乘积中

元素的个数。当环境的状态集合S，Agent可能的动作集合A较大时，Q(s,a)需要占用大量的内存空

间，而且也不具有泛化能力。

2) 采用神经网络实现Q-学习时，网络的输出对应每个动作的Q值，网络的输入对应环境状态的描

述。

神经网络保存的是输入与输出之间的映射关系，所以占用的存储空间小，同时神经网络还具有泛华

能力，但神经网络的缺点是计算量大，训练速度慢，而且还会出现“训练不足”和“过度训练” 现象。 

2.3 R-学习算法

第一个基于平均报酬模型的强化学习算法是由Schwartz 提出的R-学习算法，它是一个无模型平均

报酬强化学习算法。类似于Q-学习算法，用动作评价函数R(s,a)表达在状态s下执行以动作a为起点

的策略π的平均校准值，如式：

其中，ρπ为策略的平均报酬，

R-学习需要不断的循环，每次依据策略选择s状态下的行为a执行。

若a为贪婪动作，则ρ的更新公式：

其中，a∈(0,1)为学习率，控制动作评价函数估计误差的更新速度；β∈(0,1)为平均报酬ρ的更新学

习率。随后，Singh对这基本的R-学习算法进行了改进，用实际获得的报酬作为样本来估计平均报

酬，并在每个时间步对平均报酬进行更新。

2.4 Sarsa算法

Sarsa算法最初被称为改进的Q-学习算法，一步Sarsa算法可用下式表示：

Sarsa与Q学习的差别在于Q-学习采用的是值函数的最大值进行迭代，而Sarsa则采用的是实际的Q

值进行迭代。Sarsa 学习在每个学习步Agent依据当前Q 值确定下一状态时的动作；而Q-学习中依

据修改后的Q 值确定动作，因此称Sarsa是一种在策略TD学习。

TD-学习算法、Sarsa学习算法、Q算法-学习这些算法在小规模离散空间的强化学习任务中有着非

常出色的表现。

2.5 函数近似强化学习

虽然基于表格的经典算法（如TD算法、Q学习算法、Sarsa学习算法）在小规模离散空间的强化学

习任务上表现不错，但更多的实际问题中状态数量很多，甚至是连续状态空间，这时经典强化学习

方法难以有效学习。特别对于连续状态空间离散化的方法，当空间维度增加时, 离散化得到的状态

数量指数增加, 可见基于表格值的强化学习算法不适用于大规模离散状态或者连续状态的强化学习

任务(造成维度灾难)。

克服维度灾难的方法有：

1）分层强化学习  把一个强化学习问题分解成一组具有层次的子强化学习问题，降低了强化学习问

题的复杂度。

2）迁移强化学习  侧重于如何利用一个已学习过的强化学习问题的经验提高另一个相似但不同的强

化学习问题的学习性能。

3）函数近似  将策略或者值函数用一个函数显示描述。

根据函数近似的对象不同划分，可以分为策略搜索和值函数近似。策略搜索指直接在策略空间进行

搜索，又分为基于梯度的方法和免梯度方法。

基于梯度的方法：从一个随机策略开始, 通过策略梯度上升的优化方法不断地改进策略；例如：策

略梯度方法、自然策略梯度方法、自然演员-评论员方法等。

免梯度方法: 从一组随机策略开始, 根据优胜劣汰的原则, 通过选择、删除和生成规则产生新的一组

策略，不断迭代这个过程以获取最优策略。例如：遗传算法、蚁群优化算法等。

值函数近似:值函数近似指在值函数空间进行搜索，又分为策略迭代和值迭代。

策略迭代：从一个随机策略开始，通过策略评估和策略改进两个步骤不断迭代完成。例如：最小二

乘策略迭代、改进的策略迭代等。

值迭代：从一个随机值函数开始，每步迭代更新改进值函数。由于天然的在线学习特性，值迭代是

强化学习研究中的最重要的研究话题。

而根据函数模型的不同划分，函数近似包括基于线性值函数近似的强化学习、基于核方法的强化学

习、基于加性模型的强化学习和基于神经网络的强化学习。

3. 强化学习应用

强化学习在大空间、复杂非线性系统中具有良好的学习性能，使其在实际中获得越来越广泛的应

用。强化学习主要集中在有限资源调度，机器人控制、棋类游戏自动驾驶、机器人操控、推荐系

统、信息检索等应用领域。

3.1 在控制系统中的应用

倒立摆控制系统是强化学习在控制中的应用的典型实例，当倒立摆保持平衡时，得到奖励，倒立摆

失败时，得到惩罚。Williams 等人采用 Q 学习算法对倒立摆系统进行实验研究，并与 AHC 方法进

行比较分析。Tased以 Dyan Q 学习结合 BP 神经网络给出了一个生物反应控制实例；Klopf 以二自

由度的机械手控制为例，研究了强化学习在非线性系统自适应控制上的实用方法；Berenji 采用硬

件实现一种动作评价随机学习方法，成功完成了插栓入空任务和小球平衡器的控制任务。

3.2 在游戏比赛中的应用

游戏比赛在人工智能领域中始终是一个研究的问题，许多学者也正研究把强化学习理论应用到游戏

比赛中。最早应用的例子是Samuel的下棋程序，在强化学习用于单人游戏方面近年最受关注的工

作, 是2013 年Google DeepMind 团队在NIPS的深度学习Workshop 上提出的DQN (Deep Q-

networks) 算法 通过直接输入游戏的原始视频作为状态进行强化学习, 在雅达利" (Atari) 游戏平台中

7 款游戏的6 款上都超过了以往的算法, 并在其中3 款游戏超过了人类水平。该工作2015 年扩展发

表在Nature 上, 在49 款游戏上达到了人类水平。

3.3 在人工智能问题中的应用

强化学习算法与理论的研究为人工智能的复杂问题求解开辟了一条新的途径，强化学习的基于多步

序列决策的知识表示和基于尝试与失败的学习机制能够有效地解决知识的表示和获取的问题。目

前，强化学习在人工智能的复杂问题求解中已经取得了若干研究成果，其中有代表性的是Tesauro

的TD-Gammon 程序，该程序采用前馈神经网络作为值函数逼近器，通过自我学习对弈实现了专家

级的Back-Gammon 下棋程序。其他的相关工作包括Thrun研究的基于强化学习的国际象棋程序，

并取得了一定的进展。

3.4 在调度管理中的应用

调度是一个随机优化控制问题的例子，具有很大的经济价值。Crites和Barto将强化学习算法用于一

个 4 个电梯、10 层楼的系统中。每一个电梯都有各自的位置、方向、速度和一系列表示乘客要离

开的位置状态。这个系统的状态集合超过 1022个，用传统的动态规划方法（如值迭代法）很难管

理。Crites和Barto采用平均等待时间的平方作为电梯调度算法的性能，用反川算法训练表示Q函数

的神经网络，与其它算法相比较，强化学习更加优越。

3.5 在机器人领域中的应用

近年来国际上兴起了把强化学习应用到智能机器人行为学习的领域，其中包括单个自主机器人行为

的学习和多个机器人群体行为的学习。Maes和Brooks在“六腿”机器人的行走研究中，提出一个分

布式学习机理来进行行为选择学习，事先定义一个行为集和相应的二进制的感知状态集，根据传感

器信息反映为感知状态的“0”或“1”状态，并选择相应的行为。Santamaria和Ram提出基于case推理

的强化学习自适应反射式控制器用于移动机器人的导航控制，Hagras提出了一种既有模糊神经网

络的滞后更新多步Q学习算法实现移动机器人的导航问题，张汝波用Actor-Critic学习系统来学习移

动机器人避障问题。

Turcher Balch提出Clay控制结构应用于机器人足球赛，不同于基于行为控制结构的强化学习，他

将强化学习motor schemas有机结合，使得系统既具有强化学习的自适应能力，又有motor

schemas的实时性能。Mataric利用改进的Q学习算法实现四个机器人执行foraging任务，事先利用

领域知识将状态空间到动作空间的映射转化为条件行为来压缩状态空间的规模，加速学习。

一些著名大学都建立了学习机器人实验室，比如，MIT的Learning and Intelligent Systems 实验

室，该实验室的主要兴趣包括动态环境下机器人的学习行为、理解能力等的研究；CMU 的Artificial

Intelligence 实验室，该实验室主要研究规划、知识表示以及多机器人系统和博弈论； 国内的中国

科技大学Multi-agent Systems 实验室，该实验室主要以蓝鹰仿真、蓝鹰四腿机器人为平台研究多

智能体系统；广东工业大学建立了智能机器人研究室，RoboCup 中型组比赛为实时检验平台，以

机器人足球比赛仿真组2D 或2D 比赛平台为仿真实验平台来研究多自主移动机器人的视觉子系统、

决策子系统、通信子系统和运行控制子系统等。

3.6 在多智能体中的应用

多智能体系统( multi-agent system，MAS) 是由多个Agent 构成的系统，可泛指所有由多个自治或

者半自治模块组成的系统。

典型的强化学习算法采用状态-动作来表示行为策略，因而不可避免地出现学习参数随状态变量维

数呈指数级增长的现象，即维数灾难。目前，解决维数灾难问题的方法大致有四种: 状态聚类法、

有限策略空间搜索法、值函数近似法和分层强化学习法。分层强化学习是通过在强化学习的基础上

增加抽象机制，把整体任务分解为不同层次上的子任务，使每个子任务在规模较小的子空间中求

解，并且求得的子任务策略可以复用，从而加快问题的求解速度。

3.7 在课题中的应用

①航迹规划(基于深度学习、神经网路、Q学习算法)本质上是搜索满足约束条件的最优航迹。主要

内容包括：1)  规划空间离散化     2)  用回报函数进行形式化表达     3)  策略构造

②目标识别：将Q 学习算法与UAV 未知环境下目标搜索问题相结合

强化学习在UAV 目标搜索中的应用比较少，且UAV高机动性等要求以及战场环境复杂性等特点使

得强化学习在状态动作集合的定义及行为策略选择上要比机器人更复杂。因此，以强化学习为基础

的UAV 目标搜索技术具有重要的理论研究意义和实际应用价值。

课题强化学习系统结构图

3.8 实例 

实例1：4*4棋盘中单一棋子的移动问题

该问题共有16个状态，棋子的动作包括在棋盘内向相邻的格子上移、下移、左移和右移；

问题目标：以最少的移步从初始位置到达棋盘的左上角或右下角。

问题转化：求一个动作序列，使其累积回报最大。

用Q-学习算法求解上述问题，设置一个16*4的矩阵Q-表(如全部合法操作所对应的矩阵元素设为

1，其余为某个绝对值较大的负数)，将其初始化，并设计相关参数(α、β等)。然后随机生成初始状

态，按照Q-学习算法用Q-表的值选择相应动作，同时修改Q值。经过若干个例子的运行后，Q-表将

逐步收敛，此时E(s)基本形成右表分布，其中A0＞A1＞A2＞A3，Ai表示E(s)的值。

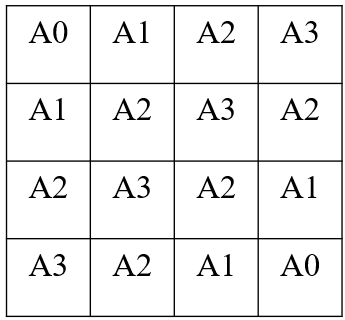
E(s)实际上反映了相应状态s的期望价值，逐步收敛后得到最优决策策略。

表示最优动作为上移；表示最优动作为下移或左移；表示最优动作为4个方向均可

实例2：TD法解决问题

一个玩家划“×”而另一个划“O”，直到一个玩家在水平、垂直或对角线方向上划上三个标记成为一行

为止。

所有能在同一直线上形成三个“×”的状态的获胜概率为1；所有在同一直线上有三个“O”，或“填满”的

状态，获胜的概率则为0；把所有其他状态的初始值设为0.5，表示有50%的机会可以获胜。

令s表示贪心走棋之前的状态，s'表示走棋之后的状态，对估计值的更新，记为V(s)

其中α是一个很小的正分数，称为步长参数，它能影响学习的速度。

在大多数情况下我们采用贪心策略，选择会导致状态值最大的走棋方式，即有最高的估计获胜概

率。但是有时候，我们也会随机选择一些其他走棋方式。这些称为探索（exploratory）走棋方式，

因为它们会引导我们去经历一些以前没有遇到过的状态。

实线表示游戏中的走棋；虚线表示我们（强化学习玩家）考虑过但是没有做出的走棋。探索性走棋

那一步不产生任何学习效果。

4. 强化学习展望

强化学习的目标是得到最大的累积奖赏。为了实现这一目标，一方面需要“利用”,即利用已经学习到

的经验来选择奖赏最高的动作，使系统向好的状态转移。另一方面，需要“ 探索”，即通过充分地掌

握环境信息，发现能得到更高奖赏的状态，避免陷入局部最优。使得强化学习方法陷入了一个“探

索-利用”困境：只有既充分地探索环境，又利用已学到的知识才能最大化累积奖赏。因此，探索–

利用的平衡成为了强化学习研究者们一直密切关注的热点。

强化学习的学习机制表明它是不断地与环境交互，以试错的方式学习得到最优策略，是一种在线学

习方法。然而，现实中有很多问题需要在离线的评估后再给出决策。目前的一个研究趋势是用离线

估计来处理上下文赌机(contextual bandit) 问题。目前已经有人建议创建强化学习的离线数据库，

可是现有的离线估计算法还不够成熟，有待进一步发展。

强化学习的另一个局限在于合适的奖赏信号定义。强化学习通过最大化累积奖赏来选择最优策

略， 奖赏很大程度上决定了策略的优劣。现阶段奖赏是由研究人员凭借领域知识定义，一个不合

理的奖赏势必会很大程度上影响最终的最优策略。有学者已经开始尝试借助人类的导师信号来改进

原有的强化学习算法，使机器人能够更好地学习到期望动作。因此，对于奖赏信号的研究将会是强

化学习未来发展的一个潜在热点。

强化学习和认知科学的交叉研究是另一个研究趋势；此外, 有模型和无模型的强化学习方法在动物

决策问题研究上得到了相应的解释，因此,以强化学习为切入点的认知模型研究将成为未来的一个

研究趋势。

强化学习在复杂、不确定系统中的优化控制问题，对于推动工业、航空、军事等各领域的发展有重

要的意义，特别是对于多自主移动机器人系统来说，强化学习是实现具有自适应性、自学习能力的

智能机器人的重要途径，为解决智能系统的知识获取这个瓶颈问题提供一个可行之法。