傅里叶变换(FT)

一个波形的傅里叶变换就是把这个波形分解成多个不同频率的正弦波之和。设h(t) 是一个给定的波形，其傅里叶积分为： H(f) = \int_{-\infty}^{+\infty} h(t) exp(-i 2\pi f t)dt
傅里叶变换的逆变换 h(t) = \int_{-\infty}^{+\infty} H(f) exp(i2\pi f t)df
傅里叶变换例题：

$\begin{matrix} h(t)=\left\{\begin{matrix} A &(|t|\leq T_0) \\ 0 &(|t|>T_0) \end{matrix}\right.\\ \\ H(f)=\int_{-T_0}^{T_0}Ae^{-i2\pi ft}dt\\ =\frac{A}{\pi T_0}sin(2\pi fT_0) \end{matrix}(1)$

$\begin{matrix} h(t)=Acos(2\pi f_0 t)\\ H(f)=\frac{A}{2}(\delta(f-f_0)+\delta(f+f_0)) \end{matrix}(2)$

离散傅里叶变换（DFT）

discrete_fourier_transform
在计算机上做傅里叶变换必须对傅里叶变换做离散化处理。离散傅里叶变换一般视作抽样后的波形的连续傅里叶变换
设函数 f(x) 在区间 0<= x <= 2\pi 上N个等分点 2\pi l/N 处的值已知，用已知周期为2\pi 的函数exp(ikx)的线性组合做 f(x) 在此区间上的三角插值函数，f(x) = \sum_{k=0}^{N-1} F_k exp(ikx)
- 并且 f(2\pi l/N) = \sum_{k=0}^{N-1} F_k exp(i2\pi kl/N),F_k 一般为一个复数
离散傅里叶变换一般具有两个性质

$\begin{matrix} \sum_{k=0}^{N-1}e^{ik2\pi/N}e^{-ik2\pi/N}=N \\ \sum_{k=0}^{N-1}e^{ijk2\pi/N}e^{-ilk2\pi/N}=0(l\neq j) \end{matrix}$

离散傅里叶变换有公式如下：

$F_k=\frac{1}{N}\sum_{l=0}^{N-1}f(2l\pi/N)e^{-ikl2\pi/N}$

离散傅里叶变换的Python 实现

import numpy as npdef DFT(x,threshold=False):N = len(x)FKR = np.zeros(N)FKI = np.zeros(N)for k in range(N):Fk_r,Fk_i = 0.0,0.0for l in range(N):angle = 2 * np.pi * k * l / NFk_r += x[l] * np.cos(angle)Fk_i -= x[l] * np.sin(angle)FKR[k] = Fk_rFKI[k] = Fk_iif threshold:for i in range(N):if abs(FKR[i])<threshold:FKR[i] = 0.0FKR[i] = round(FKR[i],5)if abs(FKI[i])<threshold:FKI[i] = 0.0FKI[i] = round(FKI[i],5)return FKR,FKI#testing
threshold = 1e-5# sin(x) example:
N = 10
X = [np.sin(i*2*np.pi/N) for i in range(N)]
FKR,FKI = DFT(X,threshold = 1e-5)#standard output
for i in range(len(FKR)):print(f"FK[{i}] = {FKR[i]} + {FKI[i]}j")

快速傅里叶变换(FFT)

注意到F_k表达式中exp(-ikl2\pi /N)的周期性，就会发先这N个F_k 中N^2个不同的项中只有N个是不同的，即:1,exp[-i2\pi/N],exp[-i4\pi/N]......
快速傅里叶算法将各项先按 exp[-ik2\pi/N]归类与合并同类项，从而将操作数从N^2 减少到 Nlog_2 N

设 N = 2^k(pos int) ，令 W = exp(-i2\pi/N) ,则W^N = 1，若记：f_l = f(2\pi l/N)/N
则离散傅里叶变换的两个性质可以改写为：

$F_j = \sum_{l=0}^{N-1}f_lW^{jl}(j=0,1,...,N-1)$

$\begin{matrix} F_{2j_1}=\sum_{l=0}^{N/2-1}(f_l+f_{l+N/2})(W^2)^{j_1l}\\ F_{2j_1+1}=\sum_{l=0}^{N/2-1}(f_l-f_{l+N/2})W^l(W^2)^{j_1l} \end{matrix}$

快速傅里叶变换的Python实现

import numpy as npdef FFT(x):N = len(x)assert (N&(N-1))==0,f"{N} is not a power of 2"if N <= 1:return xeven = FFT(x[0::2])odd  = FFT(x[1::2])T = [np.exp(-2j * np.pi * k/N) * odd[k] for k in range(N//2)]return [even[k] + T[k] for k in range(N//2)] + [even[k] - T[k] for k in range(N//2)]# example
Num = 16
x = [np.sin(j*2*np.pi/Num) for j in range(Num)]
result = FFT(x)FKR = [np.real(c) for c in result]
FKI = [np.imag(c) for c in result]

快速傅里叶变换的C语言实现

#include <stdio.h>
#include <math.h>#define PI 3.14159265358979struct Complex 
{double real;double imag;
};void FFT(struct Complex x[], int N)
{if (N <= 1)return ;struct Complex even[N/2], odd[N/2];for (int i = 0; i < N/2; i++) {even[i] = x[2*i];odd[i] = x[2*i + 1];}FFT(even,N/2);FFT(odd, N/2);for (int k = 0; k < N/2; k++) {double angle = -2 * PI * k / N;        x[k].real = even[k].real + cos(angle) * odd[k].real + sin(angle) * odd[k].imag;x[k].imag = even[k].imag + cos(angle) * odd[k].imag - sin(angle) * odd[k].real;x[k + N/2].real = even[k].real - cos(angle) * odd[k].real + sin(angle) * odd[k].imag;x[k + N/2].imag = even[k].imag - cos(angle) * odd[k].imag - sin(angle) * odd[k].real;}
}int main()
{int N = 8;struct Complex x[N] = {{1,0}, {0,0}, {1,0},{0,0}, {1,0}, {0,0}, {1,0}, {0,0}};FFT(x,N);printf("FFT result：\n");for (int i = 0; i < N; i++) {printf("FK[%d] = %.2f + %.2f i\n",i,x[i].real,x[i].imag);}
}

在编程中最复杂的就是处理复数的问题，一般使用新的struct 或者只能开动脑筋了用多个列表代替了，那样肯定会更加复杂和头晕。

傅里叶变换的应用举例

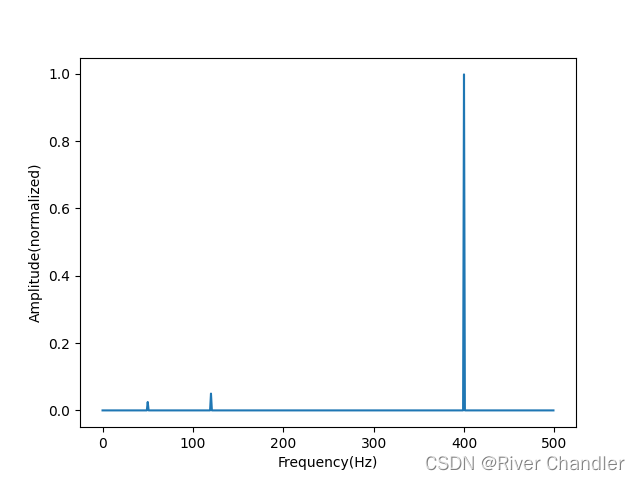
振荡频率的处理

import numpy as np
import matplotlib.pyplot as pltFs = 1000   #采样率
T = 1 / Fs  #采样间隔
L = 1000    #数据长度A1 = 1
A2 = 2
A3 = 40f1 = 50
f2 = 120
f3 = 400t = np.arange(0,L)*T  # 时间序列
data = A1 * np.sin(2*np.pi * f1 *t) +\A2 * np.sin(2*np.pi * f2 *t) +\A3 * np.sin(2*np.pi * f3 *t)#FFT变换
fft_result = np.fft.fft(data)
#频率轴
frequencies = np.fft.fftfreq(len(data),T)N = len(frequencies)
N = N //2
frequencies = frequencies[:N]
fft_result = fft_result[:N]
Norm = np.linalg.norm(np.abs(fft_result))
fft_result = np.abs(fft_result)/Normplt.plot(frequencies,fft_result)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude(normalized)")
plt.pause(0.01)Nmax = 3
max_indices = np.argsort(fft_result)[::-1][:Nmax]
# 对应的频率和幅度比例
main_frequencies = frequencies[max_indices]
main_amplitudes = fft_result[max_indices]
main_amplitudes = [i/min(main_amplitudes) for i in main_amplitudes]
print("主要频率：", main_frequencies)
print("对应幅度比例：", main_amplitudes)