全志H713/H618方案：调焦电机（相励磁法步进电机）的驱动原理、适配方法-编程知识

一、篇头

全志H713平台，作为FHD投影的低成本入门方案，其公板上也配齐了许多投影使用的模组，本文即介绍投影仪调焦所用的步进电机，此模组的驱动原理、配制方法、调试方法。
因为条件限制，本文采用的是H618香橙派Z3平台，驱动从H713上移植过来（遵循GPL协议）。

在这里插入图片描述

步进电机驱动视频-WeChat_20240225222000

二、准备工作

2.1 步进电机

在这里插入图片描述

2.2 驱动板

在这里插入图片描述

2.3 主控平台

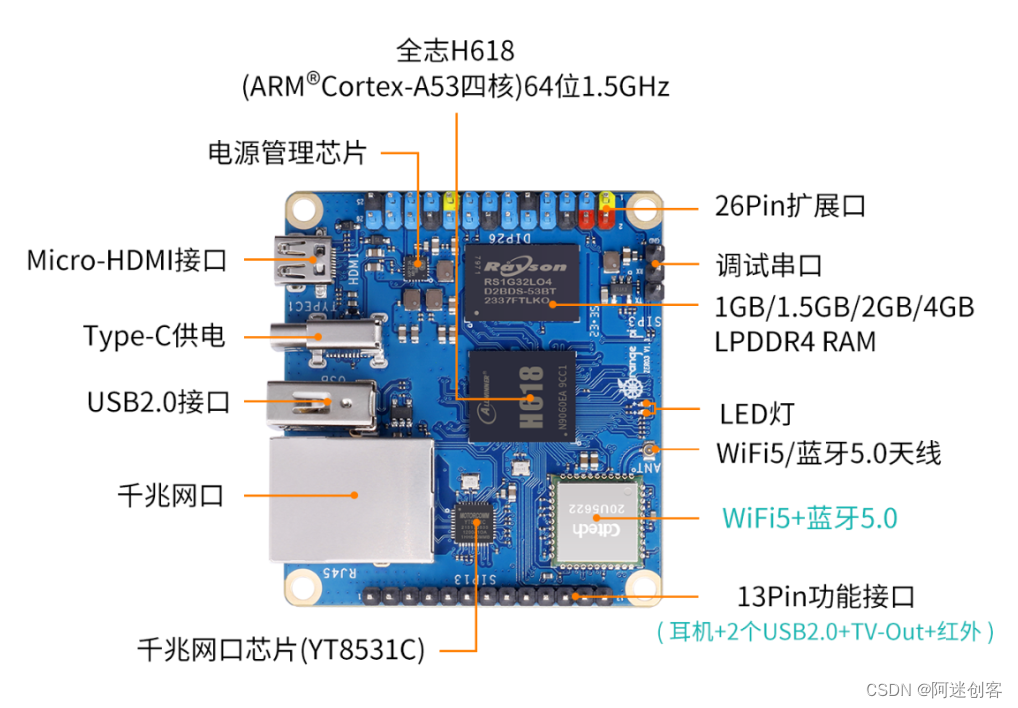
2.3.1 H618开发板(本文采用）

香橙派Z3 1G DDR

在这里插入图片描述

2.3.2 H713

缺开发板，方法和代码

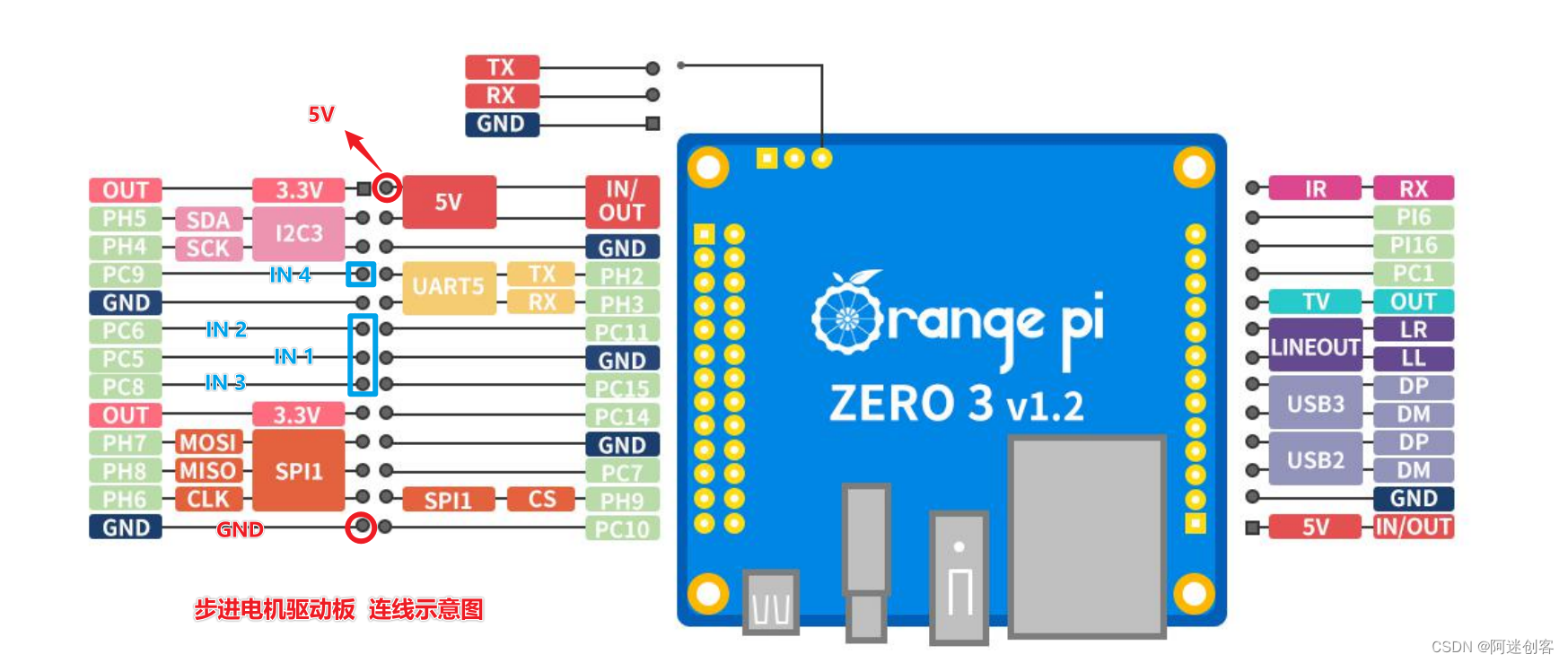
2.4 连线示意图

准备好适当的若干杜板线，将板子连接好。

GPIO PC9 --> 驱动板 IN 4
GPIO PC8 --> 驱动板 IN 3
GPIO PC6 --> 驱动板 IN 2
GPIO PC5 --> 驱动板 IN 1
最后链接5V、GND

在这里插入图片描述

三、驱动原理

3.1 驱动板原理图

在这里插入图片描述

3.2 驱动电机的方法

（1）1相励磁法: 4相4拍

每一瞬间只有一个线圈相通，其它休息。
优点：简单，耗电低，精确性良好。
缺点：力矩小，振动大，每次励磁信号走的角度都是标称角度。 1相励磁法  A->B->C->D按GPIO的说法：
GPIO-A(IN 1) 拉高，其余拉低 -> GPIO-B(IN 2)，其余拉低 -> GPIO-C(IN 3)，其余拉低 -> GPIO-D(IN 4)，其余拉低

（2）2相励磁法: 4相4拍

每一瞬间有两个线圈导通。
优点：力矩大，震动小。
缺点：每励磁信号走的角度都是标称角度。
2相励磁法  AB->BC->CD->DA按GPIO的说法：
GPIO-A/B(IN 1/2) 拉高，其余拉低 -> GPIO-B/C(IN 2/3)，其余拉低 -> GPIO-C/D(IN 3/4)，其余拉低 -> GPIO-D/A(IN 4/1)，其余拉低

（3）1-2相励磁法: 4相8拍

1相和2相交替导通。
优点）精度较高，运转平滑，每送一个励磁信号转动1/2标称角度，称为半步驱动。
1-2相励磁法  A-->AB-->B->BC->C-->CD->D-->DA按GPIO的说法：
GPIO-A(IN 1) 拉高，其余拉低 -> GPIO-A/B(IN 1/2) 拉高，其余拉低 -> GPIO-B(IN 2)，其余拉低 -> 依次类推，轮流让引脚上电、断电

3.3 用二进制表示（1-2相励磁法）

3.3.1 逆时针

u8 phase_CW[8] ={0x08,0x0c,0x04,0x06,0x02,0x03,0x01,0x09};
二进制：  1000,1100,0100,0110,0010,0011,0001,1001
ABCD视角：A000,AB00,0B00,0BC0,00C0,00CD,000D,A00D

3.3.2 顺时针

u8 phase_CCW[8]={0x09,0x01,0x03,0x02,0x06,0x04,0x0c,0x08};
二进制：  1001,0001,0011,0010,0110,0100,1100,1000
ABCD视角：A00D,0000D,00CD,00C0,0BC0,0B00,AB00,A000

3.3.3 图示

当GPIO-A拉高时，LED-A亮；拉低时，LED-A灭；其余LED与此相同，H-亮灯， L-灭灯。
上图是ULN2003步进电机驱动模块，可以看到上面的标号分别是A,B,C,D，因此代码我们可以按这个顺序来理解。
比如：AB是1100，BC是0110，CD是0011等

四、驱动实现

全志H713平台已内置此驱动。样例代码网上已有很多，此处仅取部分片段，并通过DTS的配置来详解各个参数的意义。

4.1 DTS配置

board.dts 增加如下配置，同时将其余用到PC 5,6,8,9的地方做disabled处理，避免冲突

	motor_24byj48: motor_24byj48 {compatible = "motor-control";motor-phase-num = <4>;motor-phase0-gpio = <&pio PC 5 GPIO_ACTIVE_HIGH>; //对应 IN 1，高电平有效motor-phase1-gpio = <&pio PC 6 GPIO_ACTIVE_HIGH>; //对应 IN 2motor-phase2-gpio = <&pio PC 8 GPIO_ACTIVE_HIGH>; //对应 IN 3motor-phase3-gpio = <&pio PC 9 GPIO_ACTIVE_HIGH>; //对应 IN 4motor-step-num = <8>;/* table index : b'(phase3 phase2 phase1 phase0) */motor-cw-table  = /bits/ 8 <0x09 0x01 0x03 0x02 0x06 0x04 0x0c 0x08>;motor-ccw-table = /bits/ 8 <0x08 0x0c 0x04 0x06 0x02 0x03 0x01 0x09>;motor-phase-udelay = <5>;motor-step-mdelay = <2>;status = "okay";};

4.2 驱动实现

全志H713平台已内置此驱动。

static void motor_set_phase(struct device *dev, int *gpios, int num, int phases, int delay)
{int i;int value;for (i = 0; i < num; i++) {value = (phases >> i) & 0x01;dev_dbg(dev, "set gpio %d value %d\n", gpios[i], value);gpio_set_value(gpios[i], value);udelay(delay);// dts：motor-phase-udelay}
}static void motor_set_stop(struct device *dev, int *gpios, int num)
{int i;for (i = 0; i < num; i++)gpio_set_value(gpios[i], 0);//拉低即停止
}static int motor_run_mstep(struct motor_control *motor, struct motor_workdata *data)
{int i, j;char *phase_table = NULL;switch (data->dir) {case MOTOR_DIR_CW:phase_table = motor->cw_table;//采用正转相位参数表，共8个break;case MOTOR_DIR_CCW:phase_table = motor->ccw_table;//采用反转相位参数表，共8个break;default:dev_err(motor->dev, "motor run step dir_%d error\n", data->dir);return -EINVAL;}//驱动stepsfor (i = 0; i < data->cycle; i++) {for (j = 0; j < motor->step_num; j++) {dev_dbg(motor->dev, "cycle_%d set motor phase 0x%x\n", i, phase_table[j]);motor_set_phase(motor->dev, motor->phase_gpios, \motor->phase_num, phase_table[j], motor->phase_udelay);mdelay(motor->step_mdelay);}}//驱动完成，停止motor_set_stop(motor->dev, motor->phase_gpios, motor->phase_num);return 0;
}

五、测试方法

全志H713平台已内置此驱动。

5.1 查看驱动加载情况

motor_24byj48: probe success

console:/ # dmesg | grep motor                                                 
[    0.326672] motor linux driver init ok (Version 1.0.1)
[    0.326804] motor limiter linux driver init ok (Version 1.0.1)
[    0.655092] motor-control motor_24byj48: motor-phase-num=4
[    0.661990] motor-control motor_24byj48: motor-step-num=8
[    0.668789] motor-control motor_24byj48: motor-phase-udelay=5
[    0.675967] motor-control motor_24byj48: motor-step-mdelay=2
[    0.683157] motor-control motor_24byj48: motor-phase-num 4
[    0.683161] motor-control motor_24byj48: motor-step-num 8
[    0.683169] motor-control motor_24byj48: motor-cw-table < 0x09 0x01 0x03 0x02 0x06 0x04 0x0c 0x08 >
[    0.683176] motor-control motor_24byj48: motor-ccw-table < 0x08 0x0c 0x04 0x06 0x02 0x03 0x01 0x09 >
[    0.683533] motor-control motor_24byj48: probe success
console:/ #

5.2 测试命令

5.2.1 正走100步

console:/sys/devices/platform/motor_24byj48 # echo 1,100 > motor_ctrl

5.2.2 逆走100步

console:/sys/devices/platform/motor_24byj48 # echo 2,100 > motor_ctrl

在这里插入图片描述

六、篇尾

本人从事android智能电视、投影(DLP、LCD)相关开发已有十余年，熟悉从board bringup开始，到app的全栈开发，从事过MTK、amlogic、全志、RK、高通、海奇等芯片的APP、BSP开发。目前主要工作主要集中在全志、海奇的Soc平台的技术支持工作！圈子很小，无论您是在校生、应届生、或者业内人士，有需要的多多交流，喜欢文章的朋友可以点个收藏、关注~！