1缘起

在振动分析中，对于一些高频频点的分析计算，使用包络谱技术，进而得到特化谱是最适宜的。我们看matlab信号分析中提供的一个实例：

https://www.mathworks.com/help/signal/ug/compute-envelope-spectrum.html

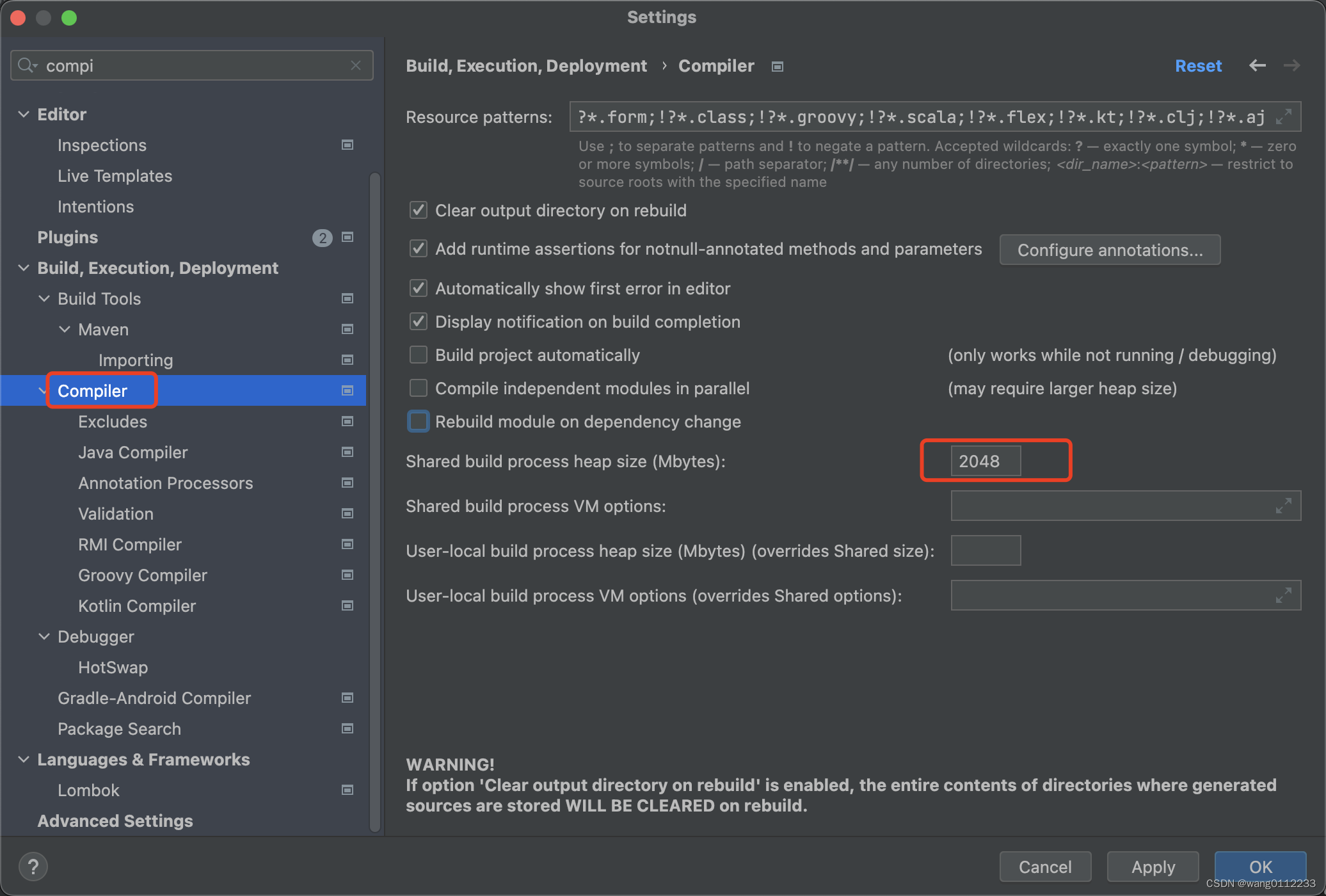
轴承故障有4个故障频点，示例中模拟了一个外圈故障的数据，然后对BPFO附近的谱线进行分解，最终用于分析的BPFO特化谱在这里：

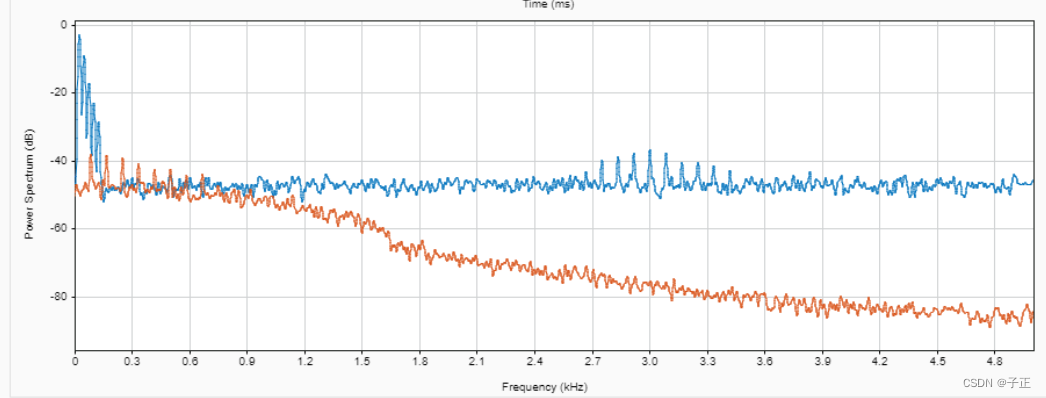
它的纵坐标有问题，最终的图理论上需要用db坐标。-40db一般认为是有效信号出现的门限。

2.包络谱的计算步骤

四个步骤：

1.去零点

2.带通滤波

3.包络解调

4.去零点

然后在展示时：

5.功率谱显示

6.设置maxFreq。修饰倍频谱线位置。

3.重要步骤备注

1.为什么最终的包络谱线能达到谱线移动的效果？

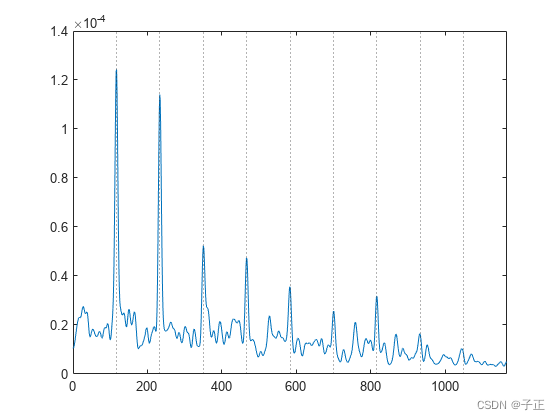
看到上面带通滤波后的红色频谱和时域图就明白了。(出处：Bandpass-filter signals - MATLAB bandpass)

经过带通之后的时域图红色的部分是个非常典型的调制波。在它的这个高频频点上BPFO的基频和倍频以调制波上叠加低频信号呈现。因为所有关心谱线之外的频段已经都被带通滤波器抑制，所以，最终经过标准的希尔伯特envelope解调后，这段细节谱就会被移动到低频部分。

注意，如果使用标准的希尔伯特解调，解调前后会有一个两倍加乘，最后生成的全域包络注意要处理掉。

附录A 各种中间波形和频谱图

原始时域图

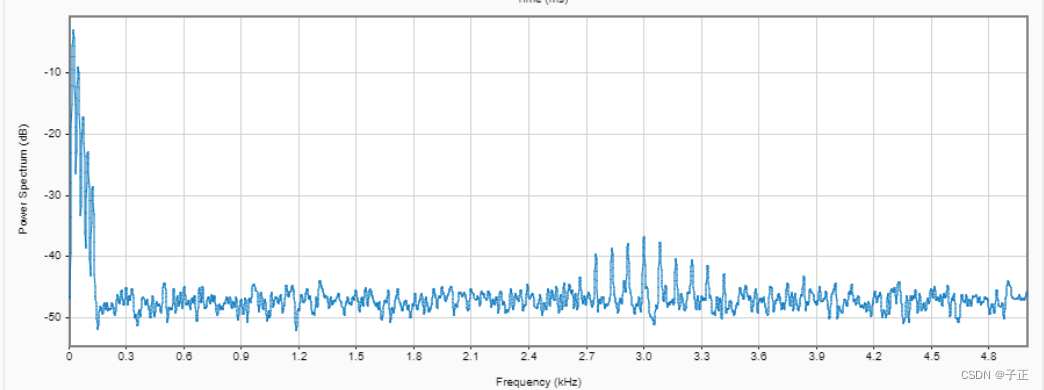
原始频域功率谱

注意3kHz的一簇梳状故障谱线，高峰已经顶过-40db。故障信号已经形成。

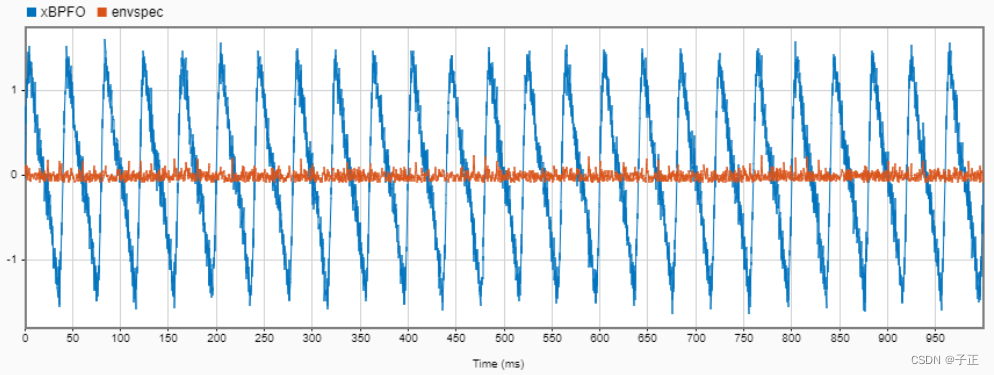
包络时域图

注意红色的故障频带幅度是很小的

包络全域频域图

这里高频的下潜部分是由带通滤波实现的，低于-40db无需分析。