题目:39_组合总数(没看题解)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
- 输入:candidates = [2,3,6,7], target = 7,
- 所求解集为: [ [7], [2,2,3] ]
示例 2:
- 输入:candidates = [2,3,5], target = 8,
- 所求解集为: [ [2,2,2,2], [2,3,3], [3,5] ]
#s
算法思想:
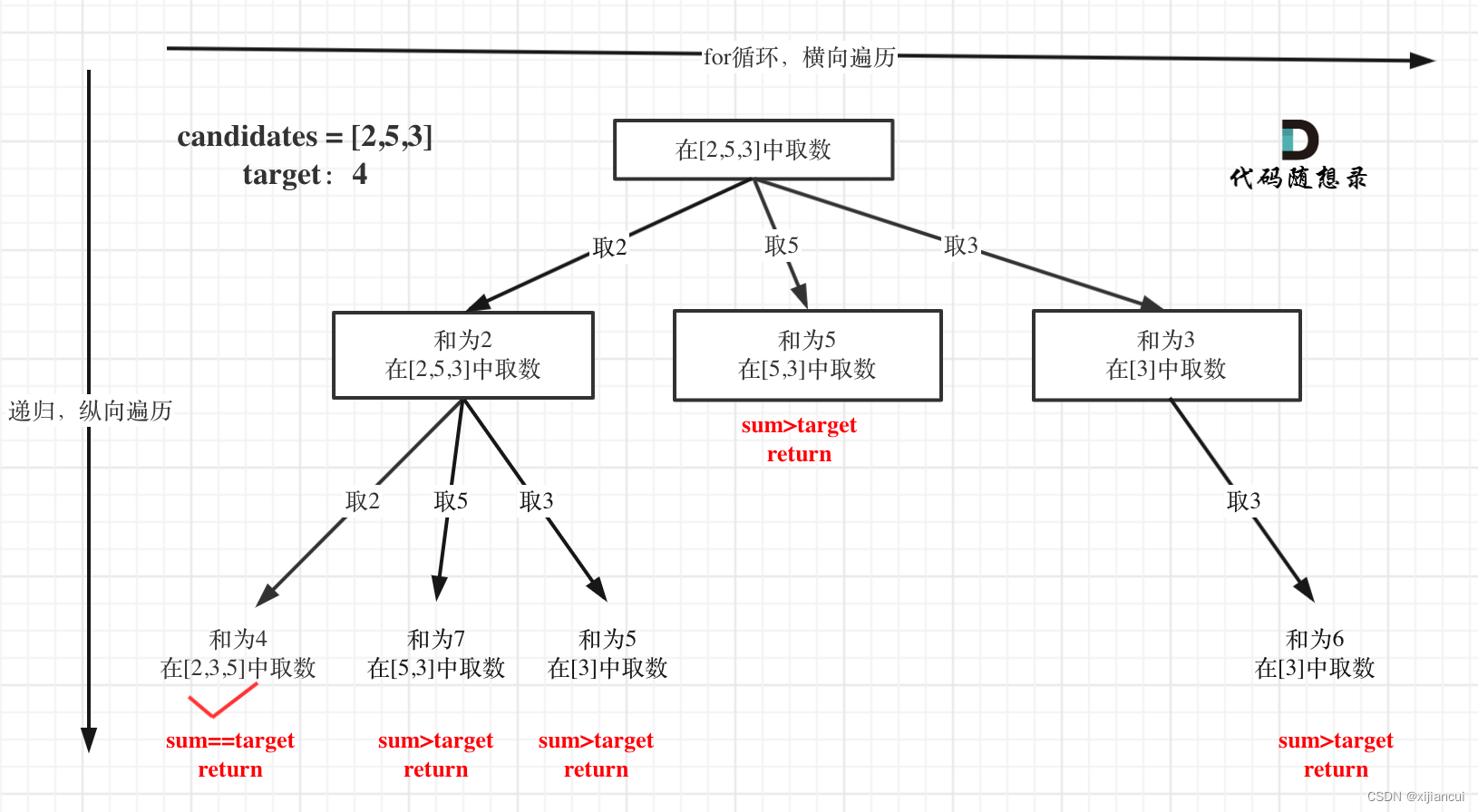
这个回溯其他地方都是一样的,只要注意递归返回的条件;
还有允许使用重复 candidate,但是结果集中,必须至少有一个数不相同,因此startindex 的值为当前处理元素,往后遍历。
代码:
import java.util.ArrayList;
import java.util.List;class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> ans = new ArrayList<>();void backtracking(int[] candidates, int target, int startindex){int sum = 0;for (int i = 0; i < path.size(); i++) {sum += path.get(i);}//递归终止条件if(sum>target) return;if(sum==target){ans.add(new ArrayList<>(path));return;}//回溯for循环for(int i = startindex;i< candidates.length;i++){path.add(candidates[i]);backtracking(candidates,target,i); //注意这里传递的startindex,就是从当前加入的值,往后path.remove(path.size()-1);}}public List<List<Integer>> combinationSum(int[] candidates, int target) {backtracking(candidates,target,0);return ans;}
}题目:40_组合总数2(看了题解)
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
- 示例 1:
- 输入: candidates = [10,1,2,7,6,1,5], target = 8,
- 所求解集为:
[[1, 7],[1, 2, 5],[2, 6],[1, 1, 6]
]
- 示例 2:
- 输入: candidates = [2,5,2,1,2], target = 5,
- 所求解集为:
[[1,2,2],[5]
]
#
算法思想:
注意这题题目特点,数组中有重复元素,但解集中不能包含重复的组合。需要去重。

回溯前先将数组排序,使数组递增有序,那么相同原声在相邻位置,同一个元素第一次出现时,就获得了包含它的所有组合,之后再出现时,如果再处理获得的就是重复组合。比如[1 , 1 , 2],获得[1, 2],如果再对 1 处理,获得[1 ,2 ]重复。
因此需要进行去重操作。
if(i>=1&&candidates[i-1]==candidates[i]&&used[i-1]==false)continue;;每次path添加元素时,把used置为true;退出回溯时,置为false。那么枝上访问1,再访问 1,都为true,可以访问;层间 访问 1 的时候,1 回溯时改为了false,直接跳过。
代码:
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> ans = new ArrayList<>();//回溯法public void backtracking(int[] candidates, int target, int startindex ,boolean[] used){int sum = 0;for (int i = 0; i < path.size(); i++) {sum += path.get(i);}//递归终止if(sum>target) return;if(sum == target) {ans.add(new ArrayList<>(path));return;}//回溯for循环for (int i = startindex; i < candidates.length; i++) {//减枝操作,若在同一层candidates[i-1]==candidates[i],则跳过该结点if(i>=1&&candidates[i-1]==candidates[i]&&used[i-1]==false)continue;;path.add(candidates[i]);used[i]=true;backtracking(candidates,target,i+1,used);path.remove(path.size()-1);used[i]=false;}}public List<List<Integer>> combinationSum2(int[] candidates, int target) {boolean[] used = new boolean[candidates.length];ArrayList<Integer> list = new ArrayList<>();for (int i = 0; i < candidates.length; i++) {list.add(candidates[i]);}//给原数组排序list.sort(new Comparator(){@Overridepublic int compare(Object o1, Object o2) {return (Integer) o1-(Integer) o2;}});for (int i = 0; i < list.size(); i++) {candidates[i]=list.get(i);}backtracking(candidates,target,0,used);return ans;}}题目:131_分割回文串(看了题解)
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]
#
算法思想:
用回溯法,分割出每一个子块,startindex 表示块首位置,i 表示块尾位置。满足回文串加入结果,不满足则 i++, 继续下一个 for 循环。startindex >= s.length 表示到字符串末尾,返回。
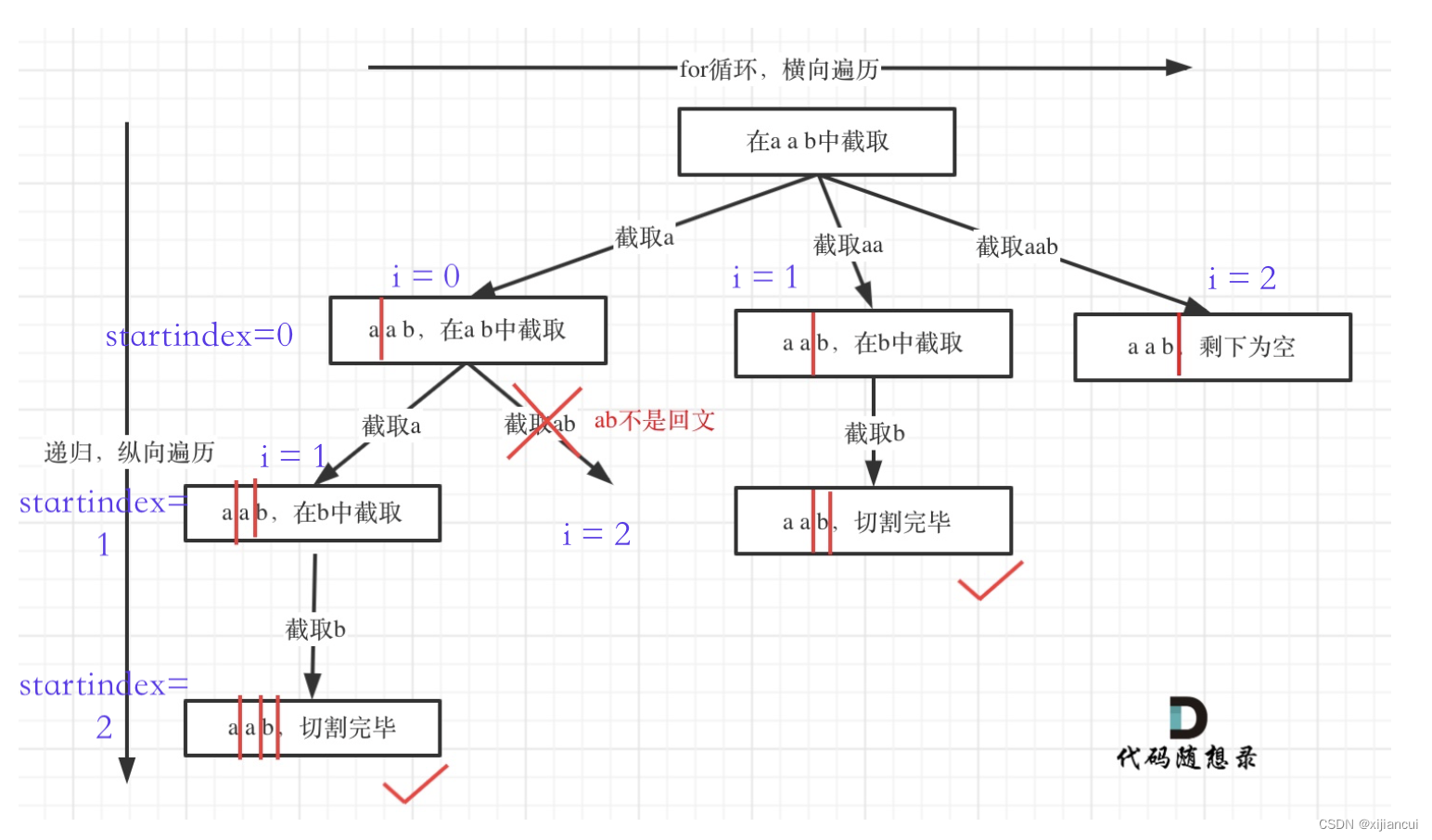
代码:
判断是否为回文串,双指针
//判断是否是回文串private boolean isPalindrome(String s, int startIndex, int end) {for (int i = startIndex, j = end; i < j; i++, j--) {if (s.charAt(i) != s.charAt(j)) {return false;}}return true;}回溯法,分割字符串
List<List<String>> lists = new ArrayList<>();List<String> str = new LinkedList<>();public List<List<String>> partition(String s) {backtracking(s, 0);return lists;}public void backtracking(String s, int startindex){//递归终止条件//startindex >= s.length 表示切完了整个字符串返回if(startindex>=s.length()){lists.add(new ArrayList<>(str));return;}//层间遍历for(int i =startindex ;i<s.length();i++){if(isPalindrome(s,startindex,i)){String temp = s.substring(startindex,i+1);str.add(temp);}else{continue;}backtracking(s,i+1);str.remove(str.size()-1);}}






![[计算机网络]--IP协议](https://img-blog.csdnimg.cn/direct/fb0769f9c27e47fab3a7ddca05213887.png)