文章目录
- [1.修剪二叉搜索树(https://leetcode.cn/problems/trim-a-binary-search-tree/description/)
- 2.将有序数组转换为二叉搜索树
- 3.把二叉搜索树转换为累加树
[1.修剪二叉搜索树(https://leetcode.cn/problems/trim-a-binary-search-tree/description/)
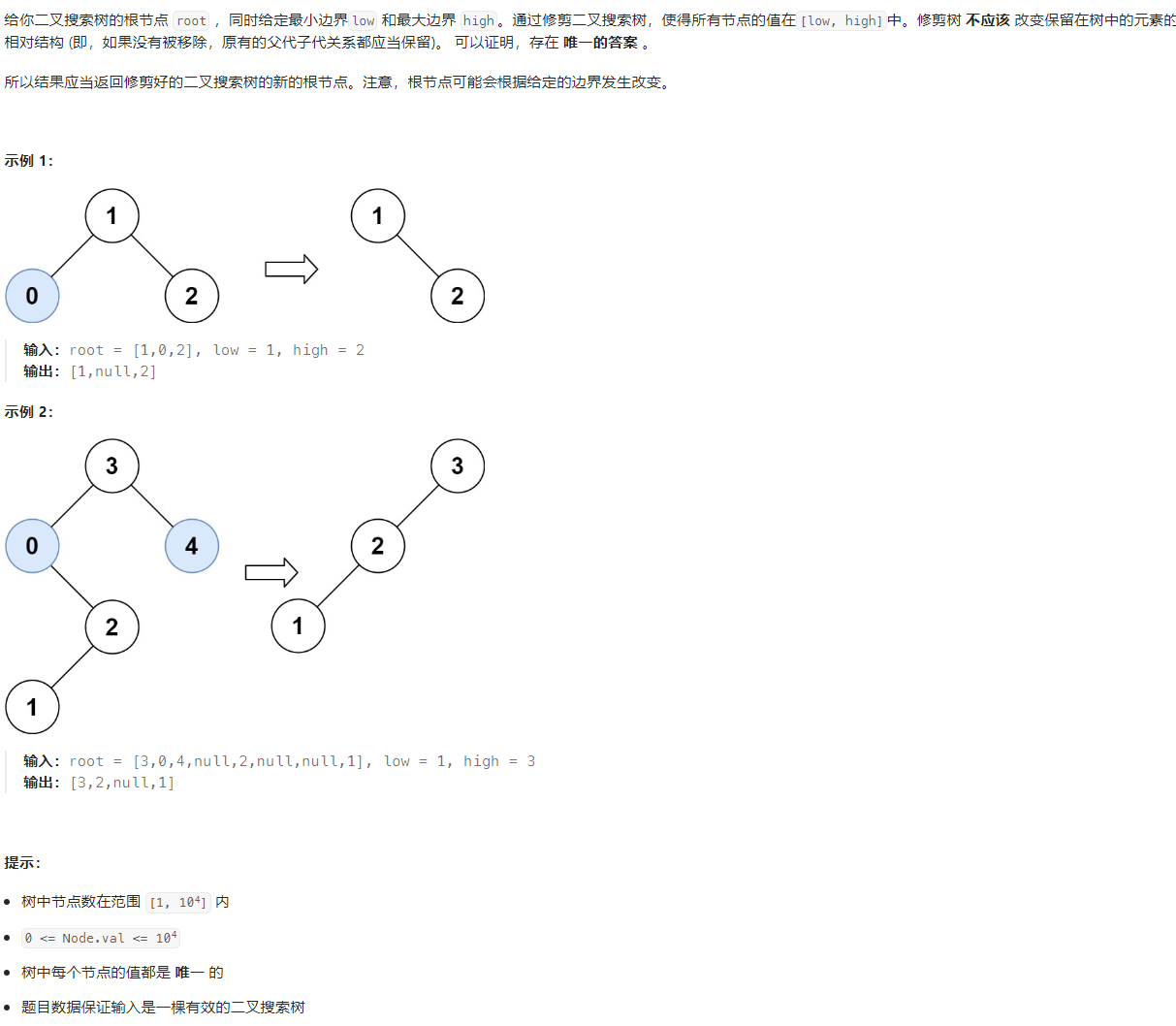
遇到超范围节点,就遍历他的下一个节点,直到找到符合范围的节点赋给符合范围的父亲节点。
代码如下
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr ) return nullptr;if (root->val < low) {TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点return right;}if (root->val > high) {TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点return left;}root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子return root;}
};
2.将有序数组转换为二叉搜索树
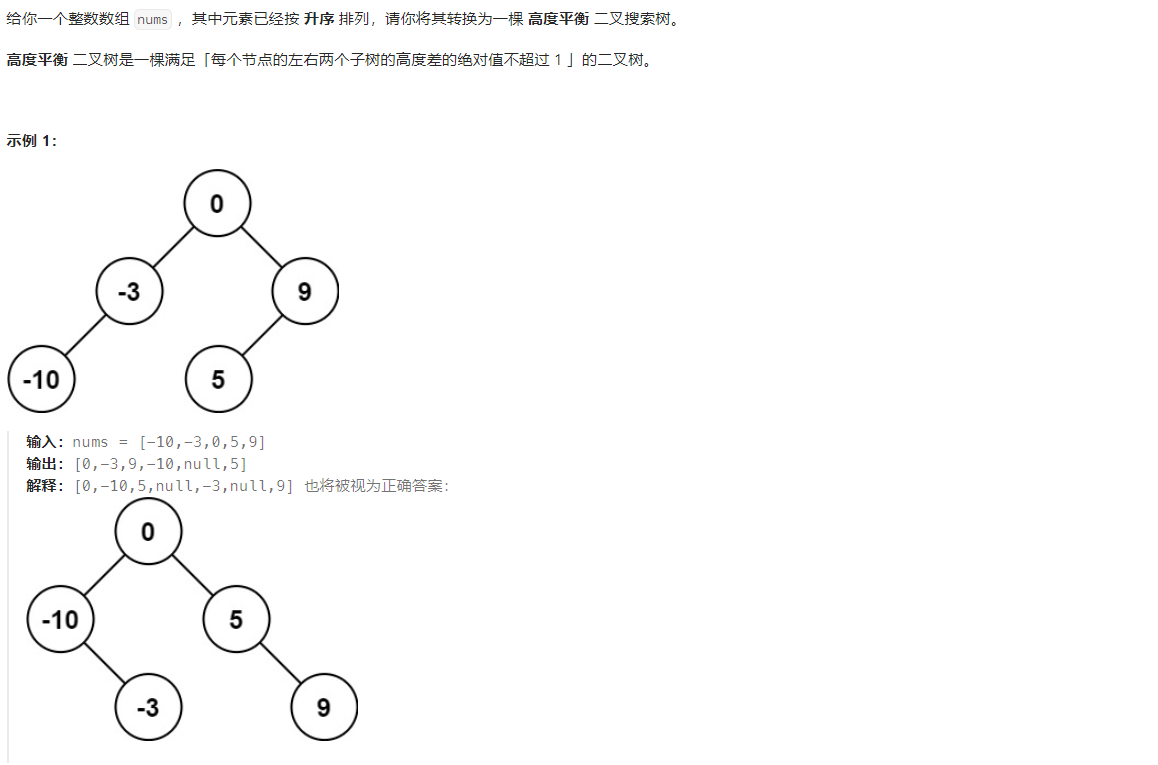
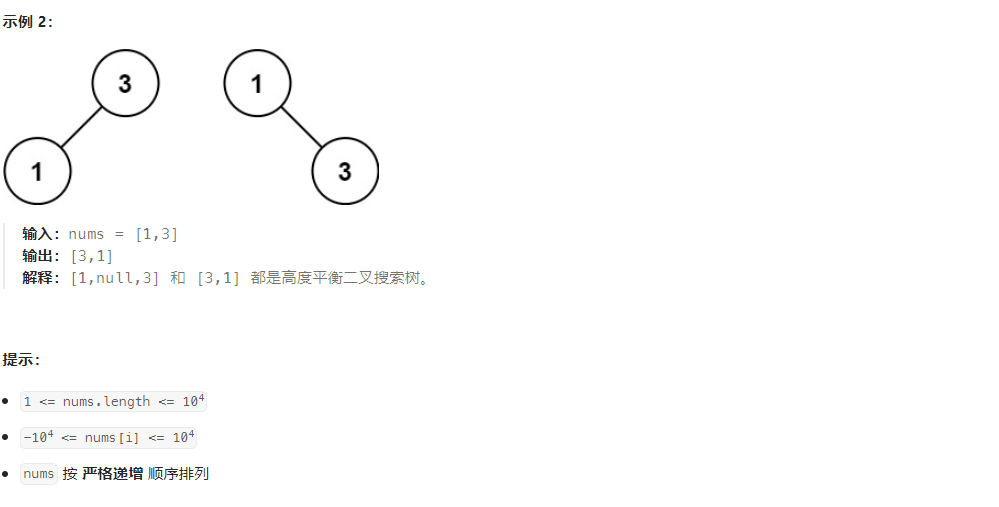
这道题重点就是寻找分割点
(left+right)/2,然后递归左右子区间。
1.参数和返回值:TreeNode* traversal(vector<int>& nums, int left, int right)
2.终止条件:left > right
3.单层递归逻辑:找到中间节点后,root的左孩子接住下一层左区间的构造节点,右孩子接住下一层右区间构造的节点。
代码如下
class Solution {
private:TreeNode* traversal(vector<int>& nums, int left, int right) {if (left > right) return nullptr;int mid = left + ((right - left) / 2);TreeNode* root = new TreeNode(nums[mid]);root->left = traversal(nums, left, mid - 1);root->right = traversal(nums, mid + 1, right);return root;}
public:TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode* root = traversal(nums, 0, nums.size() - 1);return root;}
};
3.把二叉搜索树转换为累加树
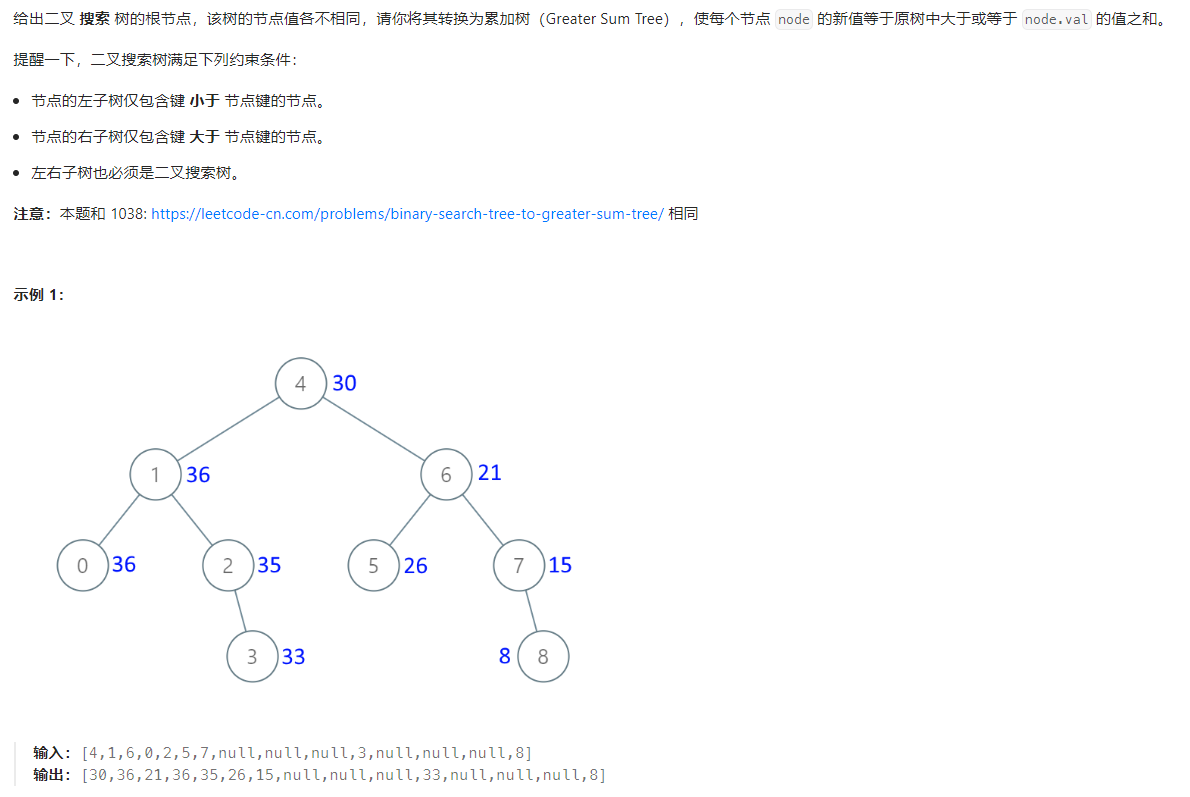

二叉搜索树累加是有序的,从最小的开始依次累加前一个节点,正序递归是中序遍历(左右中),所以累加顺序是(右中左)。
代码如下
class Solution {
private:int pre = 0; // 记录前一个节点的数值void traversal(TreeNode* cur) { // 右中左遍历if (cur == NULL) return;traversal(cur->right);cur->val += pre;pre = cur->val;traversal(cur->left);}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};