一、图论
图论是数学的一个分支,它以图为研究对象。图论中的图是若干给定的点(顶点)以及连接两点的线(边)构成的图像,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
图几乎可以用来表现所有类型的结构或系统,从交通网络到通信网络,从下棋游戏到最优流程,从任务分配到人际交互网络,图都有广阔的用武之地。
表示出最基础的图:(这些与点的大小,边的粗细都无关,只表示点与点之间通过边的关系)

二、图的基础

1.顶点(vertex)
在图的应用中,每个顶点代表的含义均不相同,而是相互通过边相联系,因此将图中的每个顶点进行标号进行区分。
①.度数(degree)
与该顶点相关联的总变数,一个图G的总度数 d(V) 等于总边数的两倍,当图的边有方向时(有向图),一个顶点的度可分为出度(out-degree)和入度(in-degree),出度是以该顶点为起点的边数,入度则是以该顶点为终点的边数。
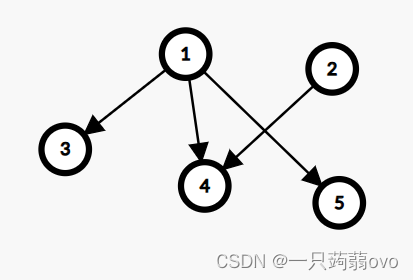
②阶数(order)
图中含有顶点的个数,即含有 n 个顶点,为 n 阶图
2. 边(edge)
顶点与顶点之间通过边联系,构成一个完整的图。
①权重(weight)
边的权重(权值),即每条边都有与之对应的值。
例如将两个顶点看成两个地点,边看成两个地点之间的距离。
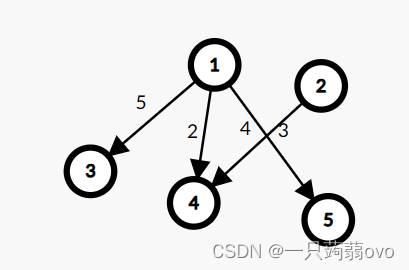
三、图的分类
综合以上,图可以分为以下几种
1.有向图/无向图
最基本的图通常被定义为“无向图”,与之对应的则被称为“有向图”。两者唯一的区别在于,有向图中的边是有方向性的。
无向边:无固定方向的边,既可 x 到 y,又可以 y 到 x
有向边:固定方向的边,即只能 x 到 y ,不能 y 到 x
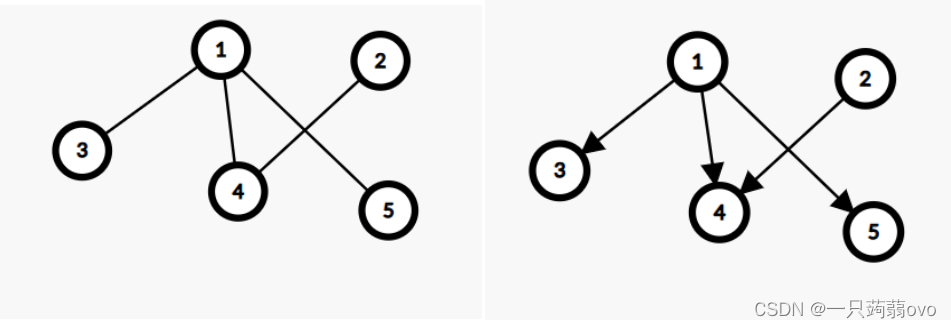
2.有权图/无权图
有权图: 权值就是一条边的长度或代价。
无权图: 不是边的权值为0,而是全都为1。
3.特殊的图——环
在图论中,环是一条只有第一个和最后一个顶点重复的非空路径。一个没有环的图被称作无环图,一个没有有向环的有向图被称做有向无环图。一个无环的连通图被称作树。
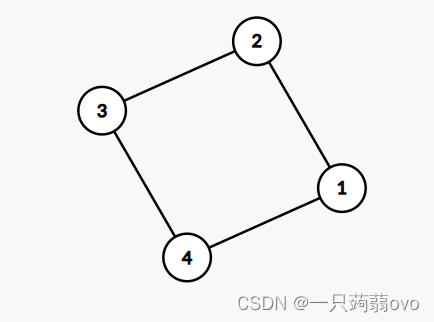
4.连通图/连通分量
在图G中,任意两个顶点之间都存在路径,则称G为连通图
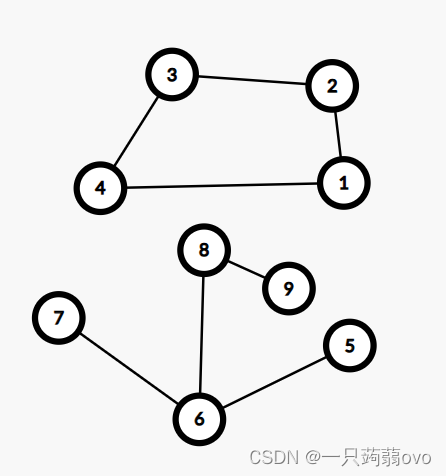
上图虽然不是一个连通图(例 点8 与 点4 不连通),但它有两个连通子图,1234,56789,
把一个图的最大连通子图称为它的连通分量。5,6,7,8,9顶点构成的子图就是该图的最大连通子图,也就是连通分量。
连通分量特点:①子图
②子图是连通的
③子图含有最大的顶点数
对于连通图而言,最大连通分量就是其本身