消息认证
消息认证 (Message Authentication):是一个证实收到的消息来自可信的源点且未被篡改的过程。
鉴别的目的
鉴别的主要目的有二:
第一,验证信息的发送者是真正的,而不是冒充的,此为信源识别;
第二,验证信息的完整性,在传送或存储过程中未被篡改,重放或延迟等。
鉴别模型
一个单纯鉴别系统的模型

鉴别系统的组成
鉴别编码器和鉴别译码器可抽象为鉴别函数。一个安全的鉴别系统,需满足
- 接收者能够检验和证实消息的合法性、真实性和完整性
- 消息的发送者和接收者不能抵赖
- 除了合法的消息发送者,其它人不能伪造合法的消息
首先要选好恰当的鉴别函数,该函数产生一个鉴别标识,然后在此基础上,给出合理的鉴别协议(Authentication Protocol),使接收者完成消息的鉴别。
鉴别函数
可用来做鉴别的函数分为三类:
- 消息加密函数(Message encryption):用完整信息的密文作为对信息的鉴别。
- 消息鉴别码MAC(Message Authentication Code):公开函数+密钥产生一个固定长度的值作为鉴别标识
- 散列函数(Hash Function):是一个公开的函数,它将任意长的信息映射成一个固定长度的信息。
加密认证
用完整信息的密文作为对信息的鉴别
对称密码体制加密认证

公钥密码体制加密认证



公钥密码体制加密认证
- 使用公开密钥加密信息的明文只能提供保密而不能提供认证。为了提供认证,发送者A用私钥对信息的明文进行加密,任意接收者都可以用A的公钥解密。
- 采用这样的结构既可提供了认证,也可提供数字签名。因为只有A 能够产生该密文,其它任何一方都不能产生该密文。
- 从效果上看A 已经用私钥对信息的明文进行了签名。
- 应当注意只用私钥加密不能提供保密性。因为,任何人只要有A的公开密钥就能够对该密文进行解密。
- 保密性与真实性是两个不同的概念。根本上,信息加密提供的是保密性而非真实性。
- 加密代价大(公钥算法代价更大)。
- 鉴别函数与保密函数的分离能提供功能上的灵活性。
广播的信息难以使用加密(信息量大)
某些信息只需要真实性,不需要保密性
消息认证码
带密钥的hash函数
适用于:通信双方基于共享的同一密钥来认证彼此之间交互的信息。
MAC 函数将密钥和数据块作为输入,产生hash值作为MAC码。
设M是变长的消息,K是仅由收发双方共享的密钥,则M的MAC由如下的函数C生成:MAC = Ck(M )
这里的Ck(M )是定长的。发送者每次将MAC附加到消息中,接收者通过重新计算MAC来对消息进行认证。
如果收到的MAC与计算得出的MAC相同,则接收者可以认为:
- 消息未被更改过
- 消息来自与他共享密钥的发送者
MAC函数类似于加密函数,主要区别在于MAC 函数不需要可逆性,而加密函数必须是可逆的,因此认证函数比加密函数更不易破解。
因为收发双方共享相同的密钥,上述过程只提供认证而不提供保密,也不能提供数字签名
MAC的基本用法



HMAC简介
ash函数用来构造MAC:HMAC为其中之一
散列函数:
概念
散列函数 (Hash Functions):一个散列函数以一个变长的报文作为输入,并产生一个定长的散列码,有时也称报文摘要,作为输出。
散列函数(又称杂凑函数)是对不定长的输入产生定长输出的一种特殊函数:h = H(M)
其中M是变长的消息
h=H(M)是定长的散列值或称为消息摘要。
散列函数H是公开的,散列值在信源处被附加在消息上,接收方通过重新计算散列值来保证消息未被篡改。
由于函数本身公开,传送过程中对散列值需要另外的加密保护(如果没有对散列值的保护,篡改者可以在修改消息的同时修改散列值,从而使散列值的认证功能失效)。
散列函数的基本用法:消息认证


散列函数的基本用法:数字签名


散列函数的基本用法:其他应用
单向口令文件
入侵检测和病毒检测
构建随机函数或伪随机函数
两个简单的Hash函数
分组对应位异或
移位分组对应位异或
Hash函数的安全需求(重点)
散列函数的目的是为文件、消息或其他的分组数据产生“指纹”。用于消息认证的散列函数H必须具有如下性质:
- 输入长度可变:H能用于任何大小的数据分组
- 输出长度固定:H都能产生定长的输出
- 效率:对于任何给定的x,H(x)要相对易于计算
- 抗原像攻击:对任何给定的散列码h,寻找x使得H(x)=h在计算上不可行
- 抗第二原像攻击:对任何给定的分组x,寻找不等于x的y,使得H(x)=H(y)在计算上不可行(弱抗冲突)
- 抗强抗攻击:寻找任何的(x,y),使得H(x)=H(y)在计算上不可行(强抗冲突)
- 伪随机性:H的输入输出满足伪随机性测试标准
散列(Hash)函数的安全性需求
Oscar以一个x开始。首先他计算Z=h(x),并企图找到一个x’满足h(x’)=h(x)。若他做到这一点,x‘也将为有效。为防止这一点,要求函数h具有无碰撞特性。
-
定义1(弱无碰撞),散列函数h称为是弱无碰撞的,是指对给定消息x∈X,在计算上几乎找不到不等于x的x’∈X,使h(x)=h(x’)。
-
定义2(强无碰撞),散列函数h被称为是强无碰撞的,是指在计算上几乎不可能找到任意的相异的x,x’,使得h(x)=h(x’)。
注:强无碰撞自然含弱无碰撞!
前两条要求具有实用性
第2条和第3条是单向性质,即给定消息可以产生一个散列码,而给定散列码不可能产生对应的消息
第4条性质是保证一个给定的消息的散列码不能找到与之相同的另外的消息,即防止伪造
第6条是对已知的生日攻击方法的防御能力。
散列函数的生日攻击
假定使用64位的散列码,是否安全?
如果采用传输加密的散列码和不加密的报文M,对手需要找到M ‘,使得H(M’)=H(M),以便使用替代报文来欺骗接收者。
一种基于生日悖论的攻击可能做到这一点。
生日问题:一个教室中,最少应有多少学生,才使至少有两人具有相同生日的概率不小于1/2?
生日问题:
假定一年按365天计算。每人生日在一年365天中的任何一天是等可能的,即都等于1/365
他们生日各不相同的概率为:
365*364*363*…*(365-n+1)/365n
因而,n个人中至少有两个人生日相同的概率为:
P = 1 - 365*364*363*…*(365-n+1)/365n
若要使P≥0.5,n = 23即可,在64人的班级中,“至少两人生日相同”的概率为0.997(n=46,p>=94.15%)
给定一个散列函数,有n个可能的输出(m位),输出值为H(x),如果H有k个随机输入,k必须为多大才能使至少存在一个输入y使得H(y)=H(x)的概率大于0.5。
对单个y,H(y) = H(x)的概率为1/n,H(y) ≠ H(x)的概率为1-(1/n)。
如果产生k个随机值y,他们之间两两不等的概率等于每个个体不匹配概率的乘积,即[1-(1/n)]k。
这样,至少有一个匹配的概率为1-[1-(1/n)]k≈1-[1-(k/n)]=k/n。要概率等于0.5,只需k=n/2=2m-1。
对长度为m位的散列码,共有2m个可能的散列码,若要使任意的x,y 有H(x)=H(y)的概率为0.5,只需k=2m/2。
散列函数的结构
由Merkle于1989年提出
Ron Rivest于1990年提出MD4
几乎被所有hash函数使用
具体做法:
把原始消息M分成一些固定长度的块Yi
最后一块padding并使其包含消息M长度
设定初始值CV0
重复使用压缩函数f,CVi = f(CVi-1,Yi-1)
最后一个CVi为hash值

MD5算法、SHA算法
MD5简介
Merkle于1989年提出hash function模型
Ron Rivest于1990年提出MD4
1992年, MD5 (RFC 1321) developed by Ron Rivest at MIT
MD5把数据分成512-bit块
MD5的hash值是128-bit
在最近数年之前,MD5是最主要的hash算法
美国标准SHA-1以MD5的前身MD4为基础
该算法以一个任意长度的报文作为输入,产生一个128bit的报文摘要作为输出。输入是按512bit的分组进行处理的。
MD5算法
MD5小结
MD5使用小数在前
Dobbertin在1996年找到了两个不同的512-bit块,它们在MD5计算下产生相同的hash
MD5不是足够安全的
MD5在线查询破解
http://www.md5.org.cn/
http://www.cmd5.com/
http://md5jiami.51240.com/
MD5的32位和16位加密算法
MD5通常是32位的编码,而在不少地方会用到16位的编码。16位就是从32位MD5散列中把中间16位提取出来。
admin 的摘要:
16位:7a57a5a743894a0e
32位:21232f297a57a5a743894a0e4a801fc3
SHA简介

SHA-512逻辑
步骤1 附加填充位:消息长为模1024与896同余
步骤2 附加长度:最后128位:128位无符号整数表明消息的长度
初始化Hash缓冲区:Hash函数的中间结果和最终结果保存在512位的缓冲区中,缓冲区用8个64位寄存器(a,b,c,d,e,f,g,h)
以1024位的分组(128个字节)为单位处理消息
输出
SHA1算法
SHA Summary
-
Applications of cryptographic hash functions
Message authentication
Digital signatures
Other applications -
Requirements and security
Security requirements for cryptographic hash functions
Brute-force attacks
Cryptanalysis -
Hash functions based on cipher block chaining
-
Secure hash algorithm (SHA)
SHA-512 logic
SHA-512 round function -
SHA-3
The sponge construction
The SHA-3 Iteration Function f
数据签名体制
数字签名(Digital Signature)是一种防止源点或终点抵赖的鉴别技术。
消息认证(Message authentication)保护双方之间的数据交换不被第三方侵犯,但它并不保证双方自身的相互欺骗。
假定A发送一个认证的信息给B,双方之间的争议可能有多种形式:
B伪造一个不同的消息,但声称是从A收到的。
A可以否认发过该消息,B无法证明A确实发了该消息。
例如:股票交易指令亏损后抵赖。
数字签名原理
一个数字签名至少应满足以下几个条件:
依赖性:数字签名必须是依赖于要签名报文的比特模式(类似于笔迹签名与被签文件的不可分离性)
唯一性:数字签名必须使用对签名者来说是唯一的信息,以防伪造和否认
可验证:数字签名必须是在算法上可验证的
抗伪造:伪造一个数字签名在计算上不可行,无论是通过以后的数字签名来构造新报文,还是对给定的报文构造一个虚假的数字签名(类似笔迹签名不可模仿性)
可用性:数字签名的产生、识别和证实必须相对简单,并且其备份在存储上是可实现的
数字签名的类别:
以方式分:
直接数字签名direct digital signature
仲裁数字签名arbitrated digital signature
以安全性分
无条件安全的数字签名
计算上安全的数字签名
以可签名次数分
一次性的数字签名
多次性的数字签名
数字签名算法
普通数字签名算法
RSA

A的公钥私钥对{KUa||KRa}
A对消息M签名: SA=EKRa(M)
问题:
速度慢
信息量大
第三方仲裁时必须暴露明文信息
hash函数的无碰撞性保证了签名的有效性
签名与加密
签名提供真实性(authentication)、加密提供保密性(confidentiality)
“签名+加密”提供“真实性+保密性”
两种实现方式: (A→B)
- 先签名,后加密: EKUb{M||SigA(M)}
- 先加密,后签名: {EKUb(M)||SigA(EKUb(M))}
方式2的问题:
发生争议时,B需要向仲裁者提供自己的私钥
安全漏洞:攻击者E截获消息,把SigA(EKUb(M))换成SigE(EKUb(M)),让B以为该消息来自E
保存信息多:除了M,SigA(EKUb(M)),还要保存EKUb(M)
∵KUb可能过期
EIGamal
EIGamal签名方案由T.ElGamal于1985年提出,其变体用于DSS中,其安全性依赖于有限域上离散对数的困难性上。
构造参数:
全局参数,p:一个大素数,g:Zp中乘法群Zp*的一个生成元。
私钥参数,x:用户的私钥,x∈Zp*
公钥参数,y:用户的公钥,y=gx mod p
算法中常还使用一个随机数k
EIGamal签名方案签名过程
给定要签名的明文M:
生成一个随机数k,k∈Zp*
计算r:r = gk mod p
计算s:s = (H(M) – xr)k-1 mod p – 1,到此,签名结果为(r,s)
把消息和签名结果(M,r,s)发给接收者
EIGamal签名方案认证过程
取得发送方的公钥y;
预查合法性:若1≤r≤p-1,继续;否则,签名不合法
计算v1:v1=yrrs mod p;
计算v2:v2=gH(M) mod p;
比较v1和v2 :如果v1=v2,表示签名有效;否则,无效
EIGamal签名方案证明:
先对s进行处理,有:
S = (H(M) – xr)k-1 mod p – 1
ks = (H(M) – xr)k-1k mod p – 1 = (H(M) – xr) mod p – 1
H(M) = xr+ks mod p – 1
考察认证过程中的等式v2 = gH(M) mod p
v2 = g xr+ks mod ( p-1) mod p = (g x)r(g k)s mod p
v2 = yrrs mod p
因为v2 = v1所以该算法成立
DSS/DSA
数字签名标准
美国国家标准与技术研究所(NIST)公布的联邦信息标准FIPS186,称为数字签名算法(DSA)。
FIPS186-3的最新版本包括三个算法
DSA
基于RSA的数字签名算法RSA-PSS
椭圆曲线的数字签名算法ECDSA
与RSA不同,DSA算法是一种密钥方案,但不能用于加密或密钥交换。DSA的安全性建立在离散对数的困难性上。

全局公开密钥分量
p:素数,其中2L-1<p<2L,512<=L<1024,且L为64的倍数:即比特长度在512到1024之间,长度增量为64比特
q:(p-1)的素因子,其中2159<q<2160,比特长度为160
g=h(p-1)/ q mod p,其中h是一整数,1<h<(p-1)
用户私有密钥
x 随机或伪随机整数,其中0<x<q
用户公开密钥
y=gx mod p
用户每个报文的密数
k随机或伪随机整数,其中0<k<q
签名
r=(gkmod p)mod q
s=[k-1(H(M)+xr)] mod q
签名=(r,s)
验证
w = (s’)-1 mod q
u1 = [H(M’)w] mod q,u2 = (r’) w mod q
v = [(gu1yu2)mod p] mod q
TEST:v = r ’
符号:
M:要签名的消息
H(M):使用SHA-1生成的M的散列码
M ',r ',s ’ :接收到的M、r、s版本
DSS签名和验证

DSS的特点
DSS的签名比验证快得多
DSS不能用于加密或者密钥分配
s-1 mod q要存在 ∅ s ≠ 0 mod q,如果发生,接收者可拒绝该签名。要求重新构造该签名,实际上,s ≡ 0 mod q的概率非常小。
若p为512位,q为160位,而DSS只需要两个160位,即320位
不可否认的数字签名算法
基本思想
一般的数字签名都是由发送方A将消息加密后送给接收方,任何一个只要知道A的公钥者都可以对此签名进行验证。
不可否认的签名是一种特殊的数字签名,它具有一些新颖的特性,没有签名者的合作,接收者就无法验证签名,在某种程度上保护了签名者的利益。
例如,软件开发者可利用不可否认的数字签名对他们的软件进行保护,使得只有付了钱的顾客才能验证签名并相信开发者仍然对软件负责。
群签名算法
群签名方案
群中各个成员以群的名义匿名地签发消息.,也称为团体签名
例:在投标中,所有投标公司组成一个团体,每个公司都用群签名方式对标书签名
群签名有如下特性:
只有群成员能代表所在的群签名
接收者能验证签名所在的群,但不知道签名者
需要时,可借助于群成员或者可信机构找到签名者
盲签名算法
假定请求签名者A,签名者(仲裁者)B。盲签名就是要求A让B签署一个文件,而不让B知悉文件的内容,仅仅要求以后在需要时B可以对他所签署的文件进行仲裁。
应用:电子货币,电子选举
盲签名的基本思想:求签名者把明文消息盲变换为M’,M’隐藏了明文M的内容;然后把M‘给签名者(仲裁者)进行签名,得到签名结果S(M’);最后,求签名者取回S(M’),采用解盲变换处理得到S(M),就是M的签名
消息->盲变换->签名->接收者->逆盲变换
盲签名协议:
采用分割-选择(Cut - and - Choose)技术,可以使签名者B知道他签署的是哪方面的信息,但是还保留盲签名的特征
例:反间谍人员化名的签名
反间谍组织的成员身份保密,甚至机构头目也不知道。机构头目还要给每个成员一个签字文件,文件的内容是:持有该文件的**人具有外交豁免权。
文件中必须使用反间谍组织的成员的化名,另外机构头目也不能对任意的文件签名。假定成员为A,机构头目是签名者B
特殊的数字签名算法
PGP
作者:Phil Zimmermann
提供可用于电子邮件和文件存储应用的保密与鉴别服务。
支持版本多。PGP支持各种系统平台和不同商业版本。
选择众所周知的算法,避免算法的安全性争议。如公钥加密包括RSA、DSS、Diffie-Hellman,对称加密包括CAST-128、IDEA、3DES、AES,以及SHA-1散列算法。
适用性强,既可用于机构,也可用于个人。
可自主使用,不由政府或标准化组织所控制。
PGP安全服务
数字签名:DSS/SHA或RSA/SHA
消息加密:CAST-128或IDEA或3DES + Diffie-Hellman或RSA
数据压缩:ZIP
邮件兼容:Radix 64转换
PGP运行流程
Ks:session key
KRa、 KUa:用户A的私钥和用户A的公钥
EP、DP:公钥加密和公钥解密
EC、DC:常规加密和常规加密
H:散列函数
Z:用ZIP算法数据压缩
R64:用radix64转换到ASCII格式
-
认证

说明:
1、 SHA-1生成消息的160的HASH码
2、SHA-1和RSA结合提供了一个高效的数字签名方案
3、DSS/SHA-1可选替代方案。 -
加密
发送方
生成消息M并为该消息生成一个随机数作为会话密钥。
用会话密钥加密M( CAST-128、IDEA或3DES )
用接收者的公钥加密会话密钥(RSA)并与消息M结合
接收方
用自己的私钥解密恢复会话密钥
用会话密钥解密恢复消息M
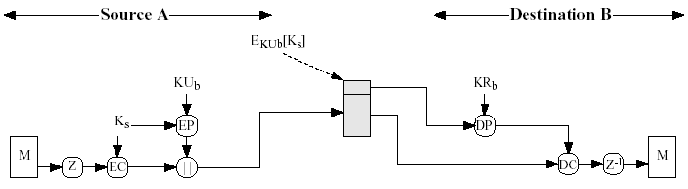
加密:保密与鉴别同时运用

-
数据压缩
压缩的位置:发生在签名后、加密前。
压缩之前生成签名:
验证时无须压缩
压缩算法的多样性
在加密前压缩:压缩的报文更难分析
对邮件传输或存储都有节省空间的好处。 -
E-mail兼容性
加密后是任意的8位字节,很多邮件系统需要ASCII正文组成的块,需要转换到ASCII格式。
Radix64将3字节输入转换到4个ASCII字符,并带CRC校验,属盲目转换(即输入流即使是ASCII,算法也会将其转换) -
分段与重组
Email常常受限制于最大消息长度(一般限制在最大50000字节)
更长的消息要进行分段,每一段分别邮寄。
PGP自动分段并在接收时自动恢复。
签名只需一次,在第一段中。
PGP消息的传送与接收

发送消息的格式

PGP密钥需求
PGP使用四种类型的密钥:一次性会话的常规密钥,公钥,私钥,基于口令短语的常规密钥。
这些密钥存在三种独立需求:
需要一种生成不可预知的会话密钥的手段
需要某种手段来标识具体的密钥。
一个用户拥有多个公钥/私钥对。(更换,分组)
每个PGP实体需要维护一个文件保存其公钥私钥对,和一个文件保存通信对方的公钥。
会话密钥的生成
以CAST-128为例。
128位的随机数是由CAST-128自己生成的。输入包括一个128位的密钥和两个64位的数据块作为加密的输入。使用CFB方式,CAST-128产生两个64位的加密数据块,这两个数据块的结合构成128位的会话密钥。
作为明文输入的两个64位数据块,是从一个128位的随机数流中导出的。这些数基于用户的键盘输入的。键盘输入时间和内容用来产生随机流。因此,如果用户以他通常的步调敲击任意键,将会产生合理的随机性。
密钥标识符
一个用户有多个公钥/私钥对时,接收者如何知道发送者是用了哪个公钥来加密会话密钥?
将公钥与消息一起传送。(浪费空间)
将一个标识符与一个公钥关联。对一个用户来说做到一一对应。(管理上带来负担)
PGP给每个公开密钥指定KeyID, KeyID由公开密钥的最低64比特组成, 包括64个有效位:(KUa mod 264)
PGP数字签名同样也需要KeyID。
密钥环
KeyID对于PGP非常关键。
两个keyID包含在任何PGP消息中,提供保密与鉴别功能。
需要一种系统化的方法存储和组织这些key以保证使用。
PGP在每一个节点上提供一对数据结构:
存储该节点拥有的公钥/私钥对;(私钥环)
存储本节点知道的其他用户的公钥;(公钥环)
私有密钥环
时间戳:密钥对生成的日期/时间;
密钥ID:公开密钥的低64位
私有密钥:密钥对的私有部分(该字段加密)
用户ID:该字段的典型值是用户的邮件地址,用户也可为每个密钥对选择不同的名字

公开密钥环
UserID:公钥的拥有者。多个UserID可以对应一个公钥。
公钥环可以用UserID或KeyID索引。

PGP —报文传输过程
签名:
从私钥环中得到私钥,利用userid作为索引
PGP提示输入口令短语,恢复私钥
构造签名部分
加密:
PGP产生一个会话密钥,并加密消息
PGP用接收者userid从公钥环中获取其公钥
构造消息的会话密钥部分

PGP —报文接收过程
解密消息
PGP用消息的会话密钥部分中的KeyID作为索引,从私钥环中获取私钥
PGP提示输入口令短语,恢复未加密的私钥
PGP恢复会话密钥,并解密消息
验证消息
用消息的签名部分中的KeyID作为索引,从公钥环中获取发送者的公钥
PGP恢复被传输过来的消息摘要
PGP对于接收到的消息作摘要,并与上一步的结果作比较

公钥管理问题
由于PGP重在广泛地在正式或非正式环境下应用,没有建立严格的公钥管理模式。
如果A的公钥环上有一个从BBS上获得B发布的公钥,但已被C替换,这是就存在两条通道。C可以向A发信并冒充B的签名,A以为是来自B;A与B的任何加密消息C都可以读取。