【GAD】动态图的半监督异常检测-编程知识

SAD: Semi-Supervised Anomaly Detection on Dynamic Graphs

Limitations of existing semi-supervised methods
Contribution
Related work
Method
- Deviation Networks with Memory Bank
- Contrastive Learning for Unlabeled Samples
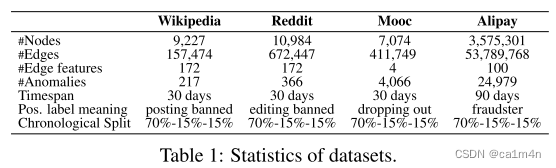
Experiments
- 少样本评估
- 2D t-SNE可视化
- 消融实验
mark

在这里插入图片描述
IJCAI2023
蚂蚁集团&中山大学
Code

Limitations of existing semi-supervised methods

没有利用大规模未标记样本
没有挖掘动态信息

Contribution

一个end-to-end的半监督异常检测框架，SAD（semi-supervised anomaly detection），采用配备时间的内存库和伪标签对比学习模块，以有效解决动态图上的异常检测问题。
使用未标记样本的统计分布作为损失计算的参考分布，并相应地生成伪标签来参与监督学习，从而充分挖掘未标记样本的潜力。
大量的实验证明了所提出的框架相对于强基线的优越性。更重要的是，我们提出的方法还可以显着缓解实际应用中的标签稀缺问题。

Related work

最近的一项工作建议采用半监督学习，通过使用来自相关下游任务的少量标记样本来解决无监督学习往往会产生噪声实例的问题。

SemiGNN [Wang et al., 2019] 学习具有分层注意力机制的多视图半监督图，用于欺诈检测。 GDN [Ding et al., 2021] 采用偏差损失来训练 GNN，并使用跨网络元学习算法进行少样本节点异常检测。 SemiADC [Meng et al., 2021] 同时探索时间序列特征相似性和基于结构的时间相关性。 TADDY [Liu et al., 2021] 构造一个节点编码来覆盖空间和时间知识，并利用唯一的transformer模型来捕获耦合的时空信息。

然而，这些方法基于动态图的离散时间快照，不太适合连续时间动态图，并且使用线性网络映射作为特征简单地将时间信息添加到模型中，而没有考虑周期性等时间属性。

Method

动态图 $\mathcal{G}=(\mathcal{V},\Large{ \varepsilon})$
令 $\Large{\varepsilon}=\left \{ \delta{(t_1)}, \delta{(t_2)},\dots ,\delta{(t_m)}\right \}$ 为生成时间网络的事件流， $m$ 为观察到的事件数，事件为 δ(t) = (vi, vj, t, xij) 表示在时间 $t$ 时从源节点$ v_i$ 到目标节点 $v_j$ 发生交互或链接，并关联边特征 $x_{ij}$ . 请注意，不同时间戳的同一对节点身份之间可能存在多个链接.

Deviation Networks with Memory Bank

为了利用few-shot labeled data进行异常检测（anomaly detector），我们按照 [Ding et al., 2021] 构建了一个图偏差网络。然而，对于动态图的应用，我们首先使用基于时间编码信息的**时间图编码器（temporal graph encoder）来学习节点表示，并另外构造一个存储库（memory bank）**来动态记录正常和未标记样本的整体统计分布作为参考分数来计算偏差损失，通过少量标记样本优化模型。整个偏差网络是半监督的，大量未标记样本用作记忆库中的统计先验，少量标记数据用于计算偏差损失。

memory bank 异常分数计算基于大多数未标记数据是正常样本的假设，产生正态样本的统计分布，作为Reference Score

受到deviation networks（利用高斯先验和基于Z-Score的偏差损失来直接优化异常分数的学习）最近成功的启发，我们采用偏差损失作为我们的主要学习目标，以强制模型在异常得分空间中分离出正常节点和特征显着偏离正常节点的异常节点。与他们的方法不同，我们使用memory bank来产生正态样本的统计分布，而不是使用标准正态分布作为参考分数。这考虑到了两个主要因素，一是真实异常分数生成的统计分布可以更好地展示不同数据集的属性，二是在动态图中，数据分布可能会因为重要的实际情况而波动更显着。节假日或周期性事件，因此不适合使用简单的标准正态分布作为正态样本的参考分布。

算reference score（均值和标准差）的时候，引入时间衰减的影响，使用时间戳 $t$ 和异常分数存储时间 $t_i$ 之间的相对时间跨度来计算每个统计示例的权重项 $w_i(t) = \frac{1}{ ln(t−t_i+1)+1}$ （也就是时间越近权重越高）
偏差损失：也就是m（异常分数）和|dev|（偏差分数）越接近越是正常；~~但是问题在于：如果异常节点（y=1)的偏差分数如果远大于m，对比损失也为0.~~ (好像dev会小于m).总之，这么计算可以保证越离群的点，deviation loss越大.
在这里插入图片描述

和我一样第一次见偏差网络的话可以看DevNet半监督异常识别模型简单学习一下

Contrastive Learning for Unlabeled Samples

为了充分利用未标记样本的潜力，我们根据现有的偏差分数 $dev(v_i, t)$ 为每个样本生成一个伪标签 $\hat{y}_i(t)$ ，并参与图编码器网络的训练。在这里，我们设计了一个有监督对比学习任务，使得偏差分数越接近的节点也具有更相似的节点表示，而偏差分数差异较大的节点在其对应的表示中具有更大的差异。
该任务的目标与我们的偏差损失一致，这使得正常样本和异常样本之间的差异在表示空间和异常得分空间上都存在偏差。
对于单个样本 $v_i$ ：
在这里插入图片描述
（投影网络将表征向量 $x$ 映射成的最终向量 $z$ ）该损失也就是达到拉近所有正样本对之间的距离，推远其他负样本对的目的.

有监督对比损失

Experiments

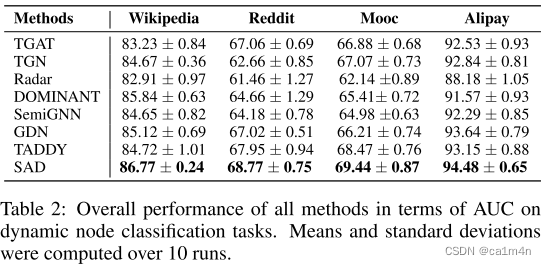
在这里插入图片描述

少样本评估

改变了丢弃率 $p$ ，即训练集中随机删除节点标签的比率，从 0.1 到 0.9，步长为 0.2.
在这里插入图片描述

值得注意的是，我们观察到当丢弃率为 0.3 时，SAD 在两个数据集上都实现了最佳性能。The result indicates that当前图数据集中存在大量冗余或噪声信息，很容易导致模型训练过拟合。通过丢弃这部分标签信息，使用伪标签数据参与训练，反而提高了模型的性能。其他方法在下降比率为 0.5 时性能显着下降。尽管如此，SAD 在两个数据集上仍然大幅优于所有基线，并且即使对于特定的大下降率（例如 0.7 和 0.9），下游性能也没有显着牺牲。

总的来说，我们认为模型的性能改进来自两个原因：

记忆库主导的异常检测器允许模型学习正常样本和异常样本之间的区别性表示；
基于伪样本的对比学习即使存在大量未标记数据，标签也有助于学习节点的通用表示。

2D t-SNE可视化

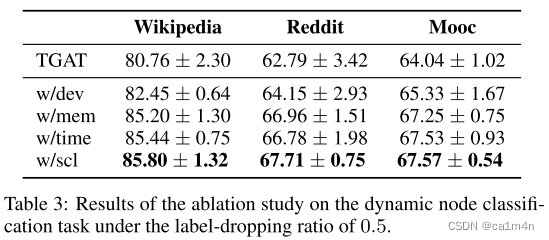
在这里插入图片描述

消融实验

在这里插入图片描述

看起来，偏差网络起了最大效果，
再加上考虑动态变化（动态图）.

mark

本文所用图偏差网络👉[Ding et al., 2021] Kaize Ding, Qinghai Zhou, Hanghang Tong, and Huan Liu. Few-shot network anomaly detection via cross-network meta-learning. In Jure Leskovec, Marko Grobelnik, Marc Najork, Jie Tang, and Leila Zia, editors, WWW’21: The Web Conference 2021, Virtual Event / Ljubljana, Slovenia, April 19-23, 2021, pages 2448–2456, 2021.

偏差网络👉Pang G, Shen C, van den Hengel A. Deep anomaly detection with deviation networks[C]//Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining. 2019: 353-362.