目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1 最小二乘正弦拟合
4.2 SNDR、SFDR 和 ENOB 计算
4.3 校正
5.算法完整程序工程
1.算法运行效果图预览

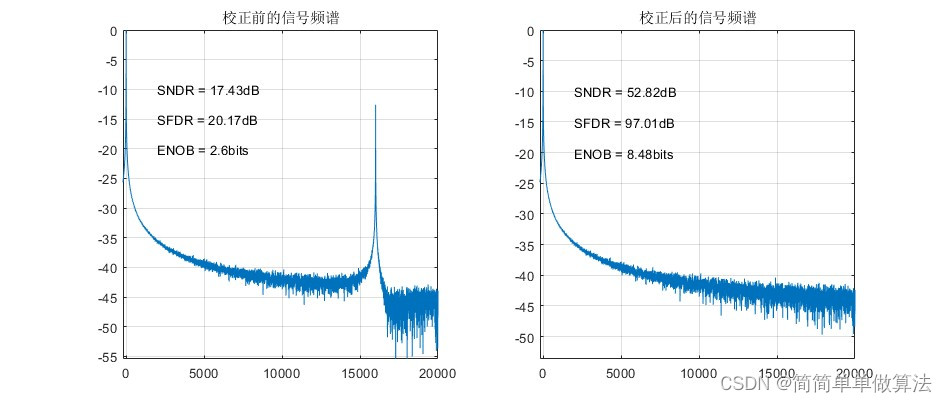
2.算法运行软件版本
matlab2022a
3.部分核心程序
.......................................................................
% 计算估计的偏置、增益和时钟误差
% 显示估计值的误差
disp('O估计误差%');
100*abs(o_-o)./o % disp('g估计误差%');
100*abs(g_-g)./g % disp('r估计误差%');
100*abs(r_-r)./r % % 使用估计结果对信号进行校正
x1_0 = (x1-o_(1))/(1+g_(1));
x2_0 = (x2-o_(2))/(1+g_(2));
x3_0 = (x3-o_(3))/(1+g_(3));
x4_0 = (x4-o_(4))/(1+g_(4)); % 单独对时钟误差进行校正
x1_ = x1_0.*cos(2*pi*fc*r_(1)/fs) - sqrt(1-x1_0.^2).*sin(2*pi*fc*r_(1)/fs);
x2_ = x2_0.*cos(2*pi*fc*r_(2)/fs) - sqrt(1-x2_0.^2).*sin(2*pi*fc*r_(2)/fs);
x3_ = x3_0.*cos(2*pi*fc*r_(3)/fs) - sqrt(1-x3_0.^2).*sin(2*pi*fc*r_(3)/fs);
x4_ = x4_0.*cos(2*pi*fc*r_(4)/fs) - sqrt(1-x4_0.^2).*sin(2*pi*fc*r_(4)/fs); % 重新组合校正后的信号
ymuxerr = zeros(size(y0)); % 注意:这里会出错,因为y0并未在代码中定义
ymuxerr(1:M:end) = x1_;
ymuxerr(2:M:end) = x2_;
ymuxerr(3:M:end) = x3_;
ymuxerr(4:M:end) = x4_; % 计算校正后信号的频谱
YMUX0err = abs(fftshift(fft(ymuxerr)));
N = length(Y0); % 注意:这里会出错,因为Y0并未在代码中定义,应该使用ymuxerr的长度
Fs = [-N/2:N/2-1]/N*fs; % 生成频率轴 % 绘制校正后的正弦信号及其频谱
figure;
subplot(211);
plot(t,ymuxerr); % 绘制时间域信号
xlim([0,0.001]); % 设置x轴范围
title('校正后的正弦信号'); % 设置标题
subplot(212);
plot(Fs,YMUX0err); % 绘制频谱
title('校正后的正弦信号频谱'); % 设置标题
xlim([0,500*fc]); % 设置x轴范围
37_008m4.算法理论概述
在信号处理领域,正弦信号是一种常见且重要的信号形式。然而,在实际应用中,由于各种噪声和失真的影响,正弦信号的幅度、频率和相位可能会发生偏差。为了准确地恢复和分析这些信号,需要采用有效的校正算法。最小二乘正弦拟合算法是一种常用的方法,它可以通过最小化误差的平方和来估计正弦信号的参数。将详细介绍该算法的原理,并通过校正幅度、频率和时钟误差来评估信号的性能,输出信噪比与失真比(SNDR)、无杂散动态范围(SFDR)和有效位数(ENOB)等指标。
4.1 最小二乘正弦拟合
假设我们有一个离散的时间序列数据 x[n],它是一个包含噪声的理想正弦波形。我们的目标是找到最接近实际数据的一个正弦函数:

解决这个优化问题可以获得最佳拟合的正弦波参数。
频率 f的估计值可用于纠正实际信号的频率偏差。时钟误差通常是相对于理想采样间隔的相对偏差,可通过频率估计来间接反映并修正。
通过拟合得到的幅度 A 可用于对原始信号进行增益调整,确保信号幅度达到期望水平。
4.2 SNDR、SFDR 和 ENOB 计算
信噪比与噪声密度比(Signal-to-Noise and Distortion Ratio, SNDR) SNDR 表示信号功率与噪声及失真功率之比,定义为:

无杂散动态范围(Spurious-Free Dynamic Range, SFDR) SFDR 是衡量系统能够同时处理大信号而保持小信号不失真的能力,通常定义为最大输出信号幅度与第二大非谐波分量幅度之间的分贝差。
有效数位(Effective Number of Bits, ENOB) ENOB 描述了ADC或DAC系统的性能,它根据SNR(仅考虑噪声)转换成相当于理想ADC的位数。若已知SNDR,可以通过以下近似公式估算ENOB:
![]()
对于基于最小二乘正弦拟合的信号校正,首先通过拟合获取纯净信号的参数,然后通过对噪声、失真项的分析,计算出SNDR和SFDR。ENOB则作为评估信号质量的关键指标,反映了经过校正后的信号接近理想量化过程的程度。
总结来说,最小二乘正弦拟合是一种强大的工具,可以帮助我们在存在噪声和失真的情况下恢复信号的真实特性,进而评估和改进信号处理系统的整体性能。在实际应用中,这些步骤可能需要结合特定的信号处理技术如FFT分析和滤波器设计来进行更精确的测量和校准。
4.3 校正
通过最小二乘正弦拟合算法得到正弦信号的参数估计值后,可以对信号的幅度、频率和时钟误差进行校正。
幅度校正:直接采用估计得到的幅度值 (A) 对原信号进行幅度校正。
频率校正:根据估计得到的频率值 (f),可以对原信号的采样率进行调整,以校正频率偏差。
时钟误差校正:时钟误差通常表现为采样时刻的偏差。如果知道精确的时钟误差值,可以对采样时刻进行插值或重采样来校正。但在实际应用中,时钟误差往往难以直接测量。一种可能的方法是通过与参考信号进行对比来估计时钟误差,并进行相应的校正。
5.算法完整程序工程
OOOOO
OOO
O