比较 1：模拟与数字滤波器

大多数数字信号源自模拟电子设备。**如果需要对信号进行滤波，是在数字化之前使用模拟滤波器，还是在数字化后使用数字滤波器更好？**将通过两个对比来回答问题。

目标是提供 1 kHz的低通滤波器。模拟端是一个六极切比雪夫滤波器，纹波为 0.5 dB （6%），其可以由 3 个运算放大器、12 个电阻器和 6 个电容器构成。在数字端，选用windowed-sinc。

模拟信号以 10 kHz 的采样率进行数字化处理，使数字频率的截止频率为 0.1。windowed-sinc 将选择为 129 点的长度，提供与模拟滤波器相同的 90% 至 10% 滚降。图 21-1 显示了这两个滤波器的频率和阶跃响应。

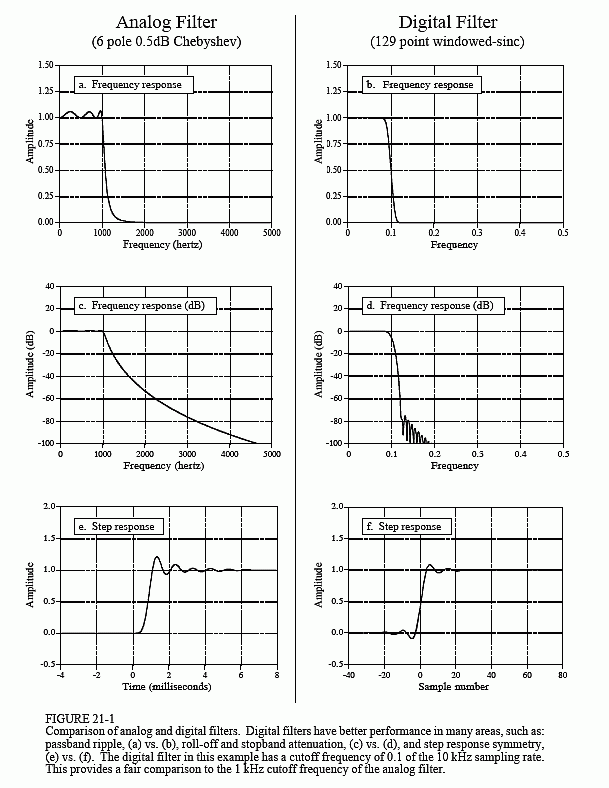
逐一比较这两个过滤器。

如（a）和（b）所示，模拟滤波器在通带内有6%的纹波，而数字滤波器则完全平坦（在0.02%以内）。模拟滤波器可实现的平坦度受其电阻器和电容器精度的限制。即使设计了巴特沃斯响应（即 0% 纹波），这种复杂性的滤波器也可能具有 1% 的残余纹波。另一方面，数字滤波器的平坦度主要受到舍入误差的限制，使其比模拟滤波器平坦数百倍。数字滤波器得一分。

接下来，查看对数刻度上的频率响应，如（c）和（d）所示。同样，数字滤波器显然是滚降和阻带衰减的胜者。即使通过增加额外的阶段来提高模拟性能，它仍然无法与数字滤波器相提并论。例如，假设需要将这两个参数提高 100 倍。这可以通过对窗口化sinc的简单修改来完成，但对于模拟电路来说几乎是不可能的。数字滤波器再打两分。

两个滤波器的阶跃响应如（e）和（f）所示。数字滤波器的阶跃响应在阶跃的下部和上部之间是对称的，即它具有线性相位。模拟滤波器的阶跃响应不对称，即它具有非线性相位。数字滤波器再加一分。最后，模拟滤波器在阶跃的一侧过冲约20%。数字滤波器过冲约10%，但在阶跃的两边。由于两者都不好，因此不授予分。

尽管有这种跳动，但仍有许多应用应该或必须使用模拟滤波器。这与滤波器的实际性能无关（即输入和输出的内容），而是与模拟电路相对于数字技术的一般优势有关：

• 第一个优点是速度：数字速度慢；模拟速度很快。例如，个人计算机只能使用 FFT 卷积以每秒约 10,000 个样本的速度过滤数据。即使是简单的运算放大器也可以在100 kHz至1 MHz的频率下工作，速度是数字系统的10到100倍！
• 与数字相比，模拟的第二个固有优势是动态范围。这有两种风格。幅度动态范围是可以通过系统的最大信号与系统固有噪声之间的比率。例如，对于约14000的动态范围，12位ADC的饱和度为4095，均方根量化噪声为0.29个数字。相比之下，标准运算放大器的饱和电压约为20伏，内部噪声约为2微伏，动态范围约为1000万。和以前一样，一个简单的运算放大器会破坏数字系统。
• 第三个是频率动态范围。例如，很容易设计一个运算放大器电路，以同时处理0.01 Hz和100 kHz（七十年）之间的频率。当使用数字系统进行尝试时，计算机会被数据淹没。例如，在 200 kHz 下采样，需要 2000 万个点才能在 0.01 Hz 下捕获一个完整的周期。数字滤波器的频率响应几乎总是绘制在线性频率标度上，而模拟滤波器通常以对数频率显示。这是因为数字滤波器需要线性刻度以显示其出色的滤波器性能，而模拟滤波器需要对数刻度来显示其巨大的动态范围。

比较 2：Windowed-Sinc vs. Chebyshev

窗口正弦滤波器和切比雪夫滤波器都设计用于将一个频段与另一个频段分开。windowed-sinc 是通过卷积实现的 FIR 滤波器，而 Chebyshev 是通过递归实现的 IIR 滤波器。哪个是频域中最好的数字滤波器？

递归滤波器的竞争者将是 0.5% 纹波、6 极切比雪夫低通滤波器。由于切比雪夫的频率响应随截止频率而变化，因此公平的比较变得复杂。将使用 0.2 的截止频率，并选择 windowed-sinc 的滤波器内核为 51 点。这使得两个滤波器具有相同的90%至10%滚降，如图21-2（a）所示。

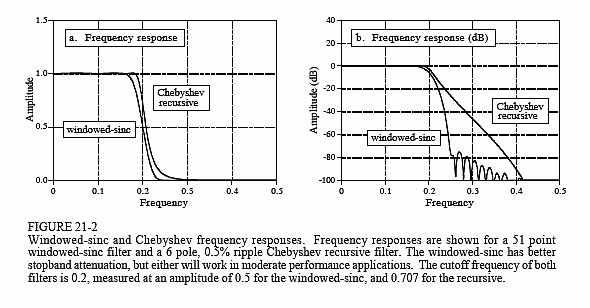
比较开始。递归滤波器在通带内有 0.5% 的纹波，而窗口正弦波是平坦的。但如果需要，可以轻松地将递归滤波器纹波设置为 0%。没有分。图 21-2b 显示，窗口 sinc 的阻带衰减比切比雪夫好得多。windowed-sinc 得 1 分。

图21-3显示了两个滤波器的阶跃响应。两者都很糟糕。递归滤波器具有非线性相位，但这可以通过双向滤波进行校正。由于这两个过滤器在这个参数中都非常丑陋，因此平局。

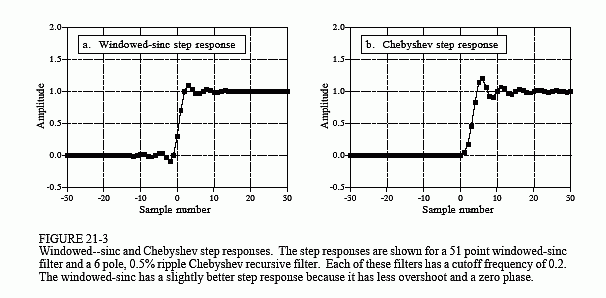
到目前为止，这两个过滤器之间没有太大区别；当需要适度的性能时，两者都可以工作。打击来自两个关键问题：最大性能和速度。windowed-sinc 是一个强大的动力源，而 Chebyshev 则快速而敏捷。假设有一个非常棘手的频率分离问题，比如说，需要隔离一个61赫兹的100毫伏信号，这个信号经过一条60赫兹的120伏电力线。

图 21-4 显示了当需要最高性能时这两个筛选器的比较情况。递归滤波器是具有 0.5% 纹波的 6 极切比雪夫。这是在 0.05 截止频率下可以以单精度使用的最大极数。windowed-sinc 使用一个 1001 点滤波器内核，该内核是通过将 501 点窗口 sinc 滤波器内核与自身卷积而形成的，提供了更大的阻带衰减。

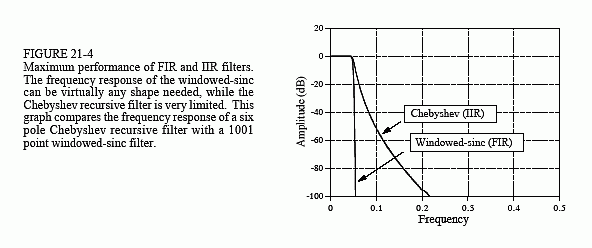
当需要最高性能时，这两个过滤器如何比较？ windowed-sinc 粉碎了切比雪夫！即使递归滤波器得到了改进（更多极点、多级实现、双精度等），它仍然无法与 FIR 性能相提并论。这就引出了第二个关键问题：速度。

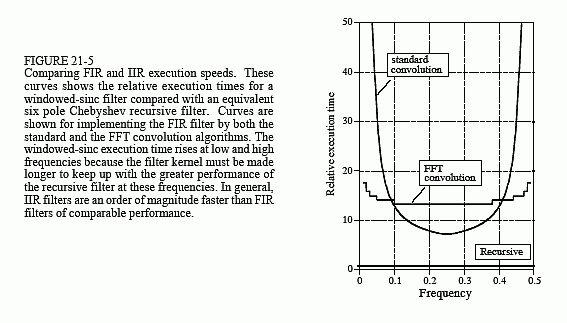
比较这些过滤器的速度就像法拉利与卡丁车比赛一样。图 21-5 显示了与六极递归滤波器相比，windowed-sinc 的执行时间。由于递归滤波器在低频和高频下具有更快的滚降速度，因此必须使windowed-sinc 内核的长度更长以匹配性能（即保持比较公平）。这解释了在频率 0 和 0.5 附近windowed-sinc 的执行时间增加的原因。重要的一点是，FIR滤波器可以预期比同类IIR滤波器慢一个数量级（卡丁车：15英里/小时，法拉利：150英里/小时）。

比较 3：移动平均线与单极线

第三场是时域滤波器之战。一个九点移动平均过滤器和使用双向技术的单极递归滤波器。为了实现相当的频率响应，单极点滤波器将使用x=0.70的样本间衰减。从图21-6开始，其中显示了每个滤波器的频率响应。两者都不是很令人印象深刻，但频率分离不是这些滤波器的用途。双方都没有分。

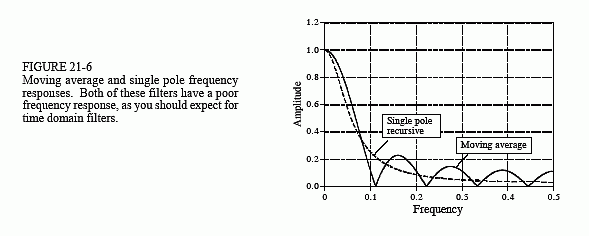
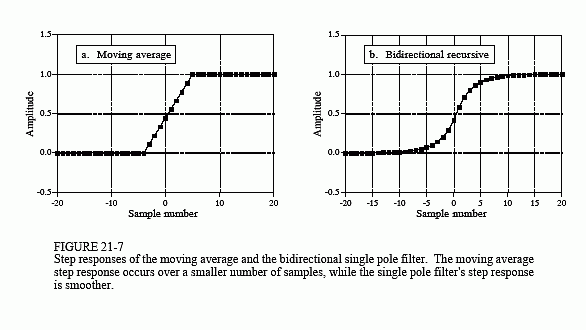
图 21-7 显示了滤波器的阶跃响应。在（a）中，移动平均阶跃响应是一条直线，这是从一个水平移动到另一个水平的最快速方式。在（b）中，递归滤波器的阶跃响应更平滑，这对于某些应用来说可能更好。每边一分。

这些过滤器在性能方面相当匹配，并且通常根据个人喜好在两者之间进行选择。在两种情况下，一个过滤器比另一个过滤器略有优势。这些基于开发时间和执行时间之间的权衡：

• 首先，希望缩短开发时间，并愿意接受较慢的筛选器。例如，可能有一次需要过滤几千个点。由于整个程序只需几秒钟即可运行，因此花时间优化算法是没有意义的。几乎肯定会使用浮点数。选择使用卷积执行的移动平均滤波器，或单极递归滤波器。这里的赢家是递归过滤器。编程和修改会稍微容易一些，并且执行速度会快得多。
• 第二种情况恰恰相反；过滤器必须尽可能快地运行，并且愿意花费额外的开发时间来获得它。例如，此过滤器可能是商业产品的一部分，有可能运行数百万次。可能会使用整数以获得尽可能高的速度。选择的过滤器将是通过递归执行的移动平均线，或使用查找表或整数数学实现的单极递归滤波器。赢家是移动平均线过滤器。它将执行得更快，并且不容易受到整数算术的发展和执行问题的影响。