这里写目录标题
- 一、78. 子集
- 1、nums = [1,2,3]为例把求子集抽象为树型结构
- 2、回溯三部曲
- 二、90. 子集 II
- 1、本题搜索的过程抽象成树形结构如下:
- 三、39. 组合总和
- 1、回溯三部曲
- 2、剪枝优化
- 四、LCR 082. 组合总和 II
- 1、思路
- 2、树形结构如图所示:
- 3、回溯三部曲
一、78. 子集
中等
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
1、nums = [1,2,3]为例把求子集抽象为树型结构
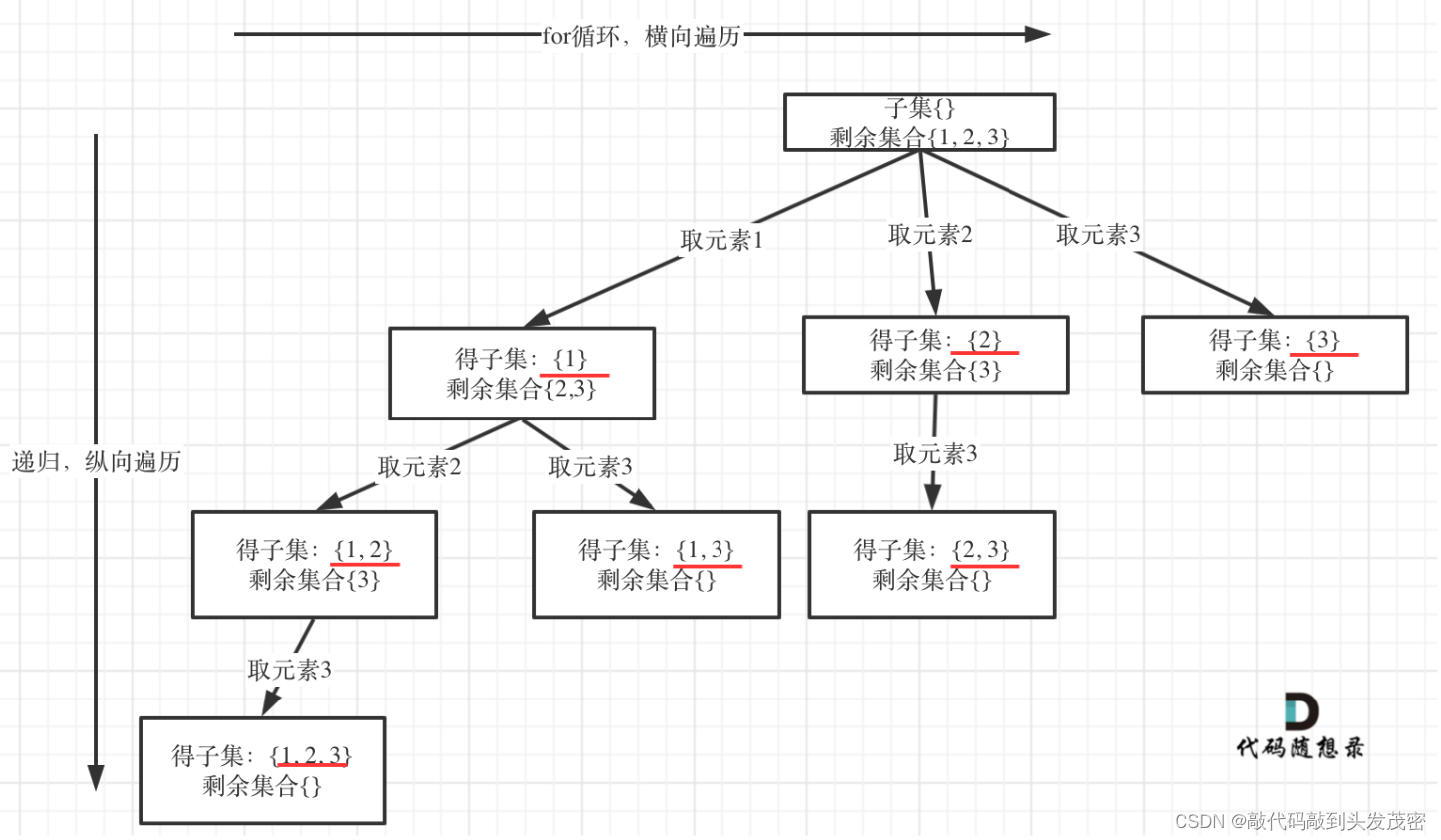
从图中红线部分,可以看出遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合。
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!
2、回溯三部曲
1、递归函数参数
全局变量数组path为子集收集元素,二维数组result存放子集组合。(也可以放到递归函数参数里)
递归函数参数在上面讲到了,需要startIndex。
剩余集合为空的时候,就是叶子节点。
那么什么时候剩余集合为空呢?
就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
class S79:def func(self,nums):result=[]def dfs(path,startIndex):result.append(path[:]) #todo 收集结果代码为什么放到这里?因为每进入一层递归需要把当前结果放入resultif startIndex>=len(nums):returnfor i in range(startIndex,len(nums)):path.append(nums[i])dfs(path,i+1) #todo i+1:保证之前传入的数,不再重复使用path.pop()dfs([],0)return resultr=S79()
nums=[1,2,3]
print(r.func(nums))二、90. 子集 II
中等
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
1、本题搜索的过程抽象成树形结构如下:

从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
startIndex的目的是不再取当前数之前的数,防止重复 [2,1]——》[1,2]重复了
class S90:def func(self,nums):result=[]def dfs(path,used,startIndex):result.append(path[:])if len(nums)==len(path):returnfor i in range(startIndex,len(nums)):if i>0 and nums[i]==nums[i-1] and used[i-1]==False:continueif used[i]==True:continueused[i]=Truepath.append(nums[i])dfs(path,used,i+1)used[i]=Falsepath.pop()dfs([],[False]*len(nums),0)return resultr=S90()
nums=[1,2,2]
print(r.func(nums))
三、39. 组合总和
中等
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
1、回溯三部曲
1、递归函数参数
这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入)
首先是题目中给出的参数,集合candidates, 和目标值target。
此外我还定义了int型的sum变量来统计单一结果path里的总和,其实这个sum也可以不用,用target做相应的减法就可以了,最后如何target==0就说明找到符合的结果了,但为了代码逻辑清晰,我依然用了sum。
本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?
我举过例子,如果是一个集合来求组合的话,就需要startIndex;
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex
2、递归终止条件
在如下树形结构中:

从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
sum等于target的时候,需要收集结果,代码如下:
if total > target:return
if total == target:result.append(path[:])return
3、单层搜索的逻辑
单层for循环依然是从startIndex开始,搜索candidates集合。
本题元素为可重复选取的。
如何重复选取呢,代码注释
for i in range(startIndex, len(candidates)):total += candidates[i]path.append(candidates[i])dfs(total, i, path) # 不用i+1了,表示可以重复读取当前的数total -= candidates[i]path.pop()
总代码:
class S39:def func(self, candidates, target):result = []def dfs(total, startIndex, path):if total > target:returnif total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):total += candidates[i]path.append(candidates[i])dfs(total, i, path)total -= candidates[i]path.pop()dfs(0, 0, [])return resultr = S39()
candidates = [2,3,6,7]
target = 7
print(r.func(candidates, target))
2、剪枝优化
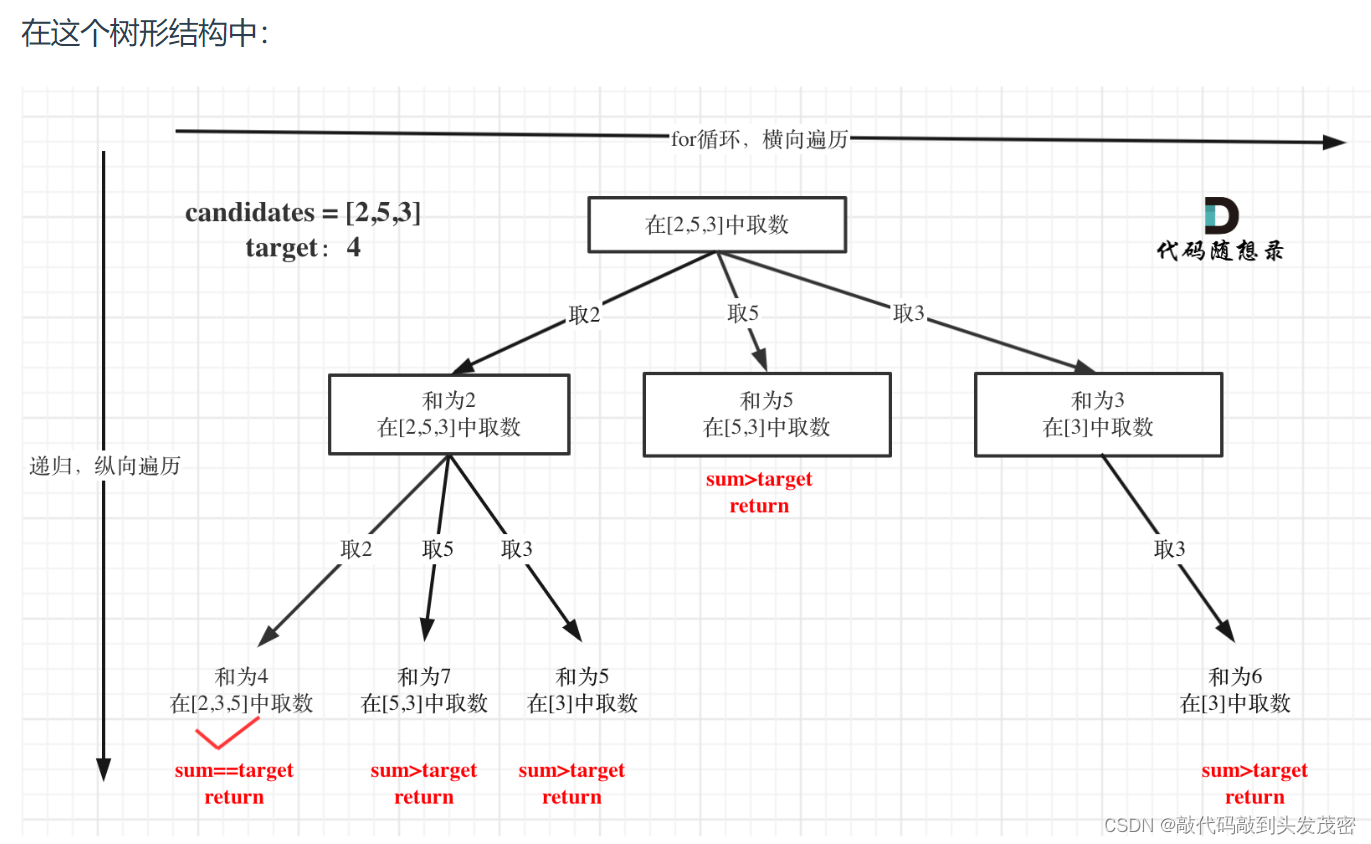
以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。
那么可以在for循环的搜索范围上做做文章了。
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。

for循环剪枝代码如下:
for i in range(startIndex, len(candidates)):if total+candidates[i]>target:continuetotal += candidates[i]path.append(candidates[i])dfs(total, i, path)total -= candidates[i]path.pop()
总代码
class S39:def func(self, candidates, target):result = []def dfs(total, startIndex, path):# if total > target:# returnif total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):if total+candidates[i]>target:continuetotal += candidates[i]path.append(candidates[i])dfs(total, i, path)total -= candidates[i]path.pop()dfs(0, 0, [])return resultr = S39()
candidates = [2,3,6,7]
target = 7
print(r.func(candidates, target))
四、LCR 082. 组合总和 II
中等
给定一个可能有重复数字的整数数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次,解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
1、思路
这道题目和39.组合总和如下区别:
本题candidates 中的每个数字在每个组合中只能使用一次。
本题数组candidates的元素是有重复的,而39.组合总和是无重复元素的数组candidates
最后本题和39.组合总和要求一样,解集不能包含重复的组合。
本题的难点在于区别2中:集合(数组candidates)有重复元素,但还不能有重复的组合。
2、树形结构如图所示:
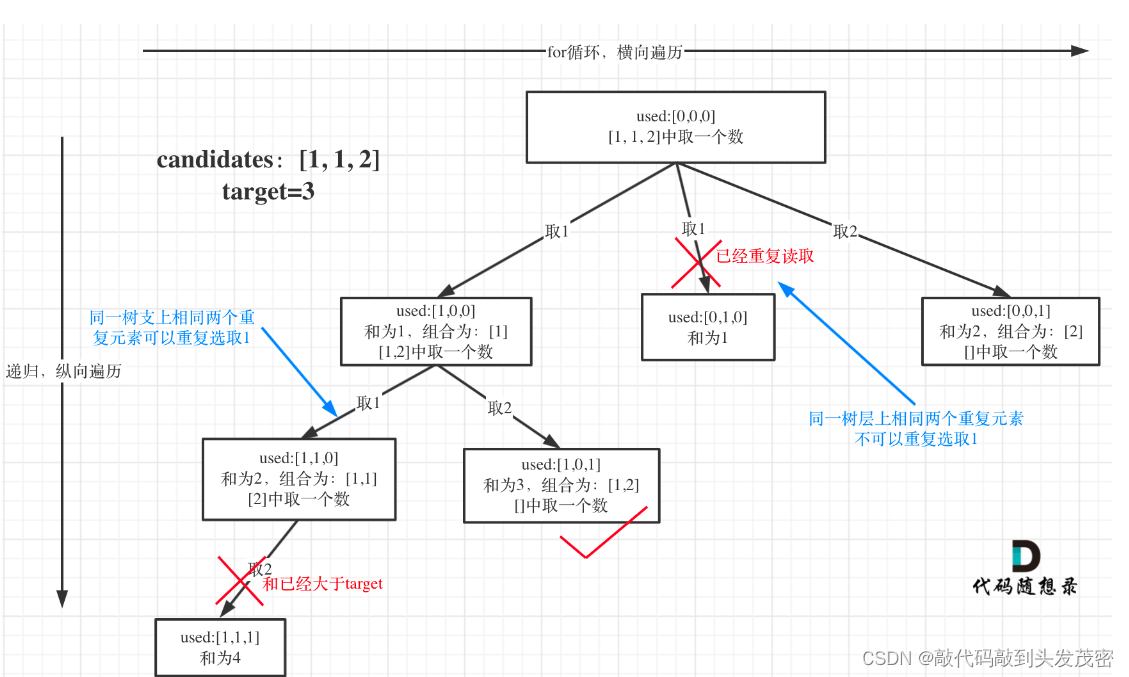
3、回溯三部曲
a、递归函数参数
与39.组合总和套路相同,此题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
这个集合去重的重任就是used来完成的。
b、递归终止条件
与39.组合总和相同,终止条件为 sum > target 和 sum == target。。
c、单层搜索的逻辑
这里与39.组合总和最大的不同就是要去重了。
前面我们提到:要去重的是“同一树层上的使用过”,如何判断同一树层上元素(相同的元素)是否使用过了呢。
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。
此时for循环里就应该做continue的操作。
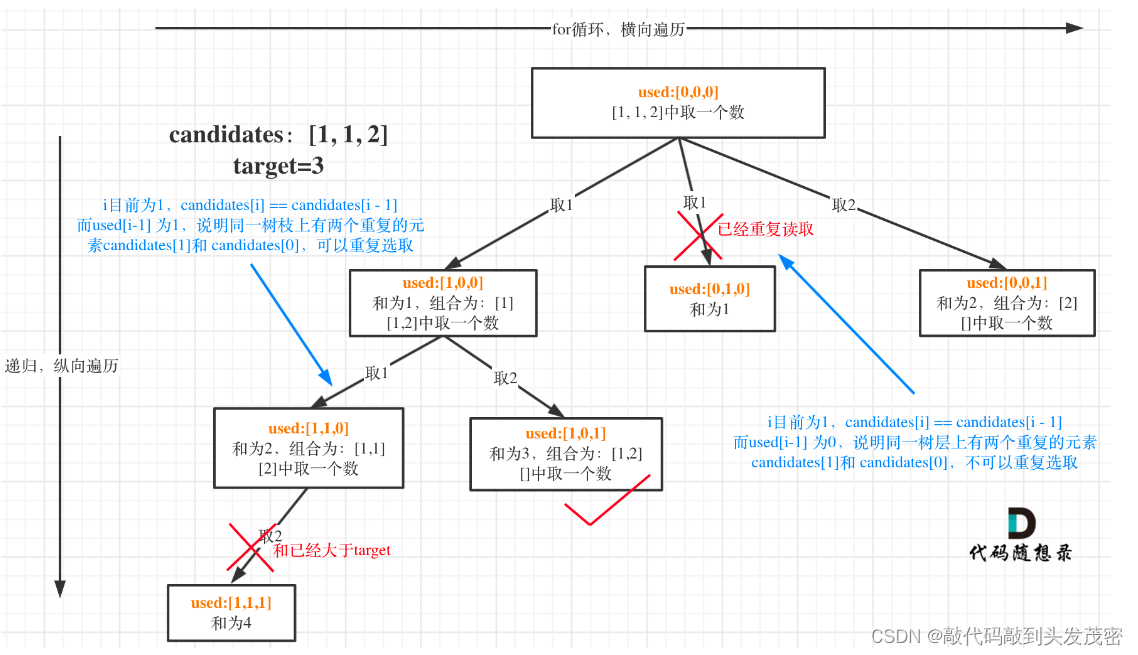
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
used[i - 1] == false,说明同一树层candidates[i - 1]使用过
可能有的录友想,为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
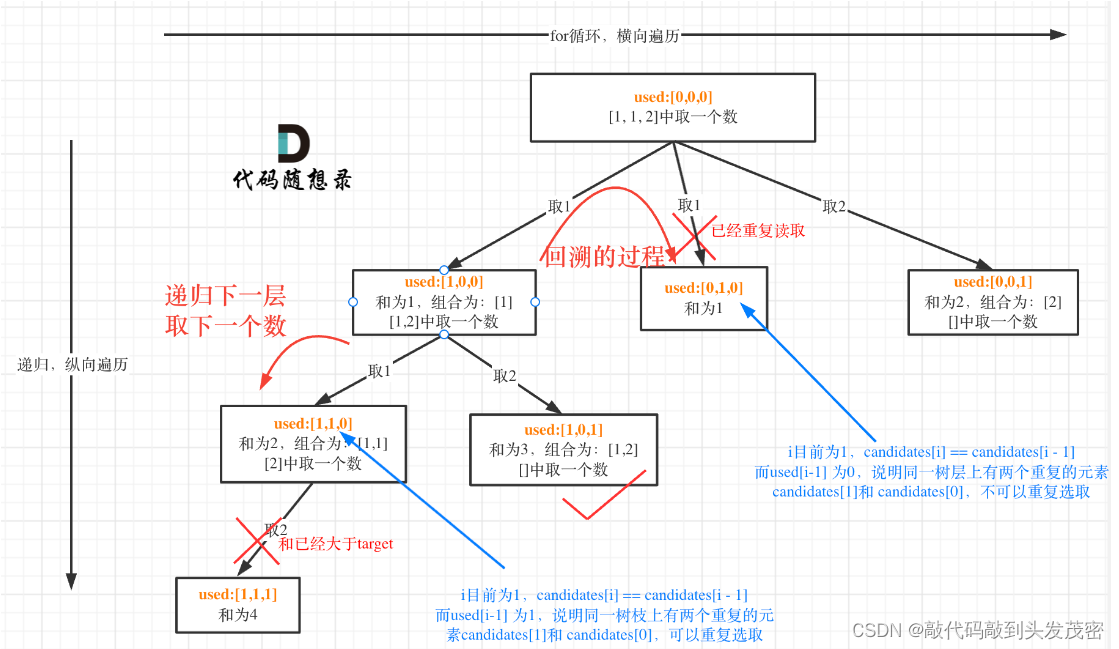
class LCR082:def func(self, candidates, target):candidates.sort()result = []def dfs(total, path, used, startIndex):if total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):if total + candidates[i] > target:continueif i > 0 and candidates[i] == candidates[i - 1] and used[i - 1] == False:continueif used[i] == True:continueused[i] = Truetotal += candidates[i]path.append(candidates[i])dfs(total, path, used, i + 1)total -= candidates[i]path.pop()used[i]=Falsedfs(0, [], [False] * len(candidates), 0)return resultr = LCR082()
candidates = [10, 1, 2, 7, 6, 1, 5]
target = 8
print(r.func(candidates, target))